Dubbelintegral

Jag undrar om någon skulle kunna förklara hur man löser uppgift (c) på ett så enkelt sätt som möjligt. Efter ett tag så lyckades jag lösa dubbelintegralen genom att dela upp området D i två vilket gav mig lösningen: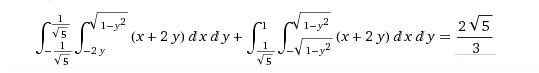 vilket är korrekt svar, men själv så tycker jag att min lösning var väldigt "jobbig" och jag gissar på att det finns något smidigare sätt. Först så tänkte jag byta till polära koordinater eftersom vi jobbar i en cirkelskiva men linjen x+2y=0 ger oss inga standardvinklar, så jag visste inte riktigt hur jag skulle lösa det. Funderade även på att göra något linjärt byte (t ex u= x^2+y^2, v=x+2y) men där visste jag inte hur jag skulle begränsa u och v.
vilket är korrekt svar, men själv så tycker jag att min lösning var väldigt "jobbig" och jag gissar på att det finns något smidigare sätt. Först så tänkte jag byta till polära koordinater eftersom vi jobbar i en cirkelskiva men linjen x+2y=0 ger oss inga standardvinklar, så jag visste inte riktigt hur jag skulle lösa det. Funderade även på att göra något linjärt byte (t ex u= x^2+y^2, v=x+2y) men där visste jag inte hur jag skulle begränsa u och v.
All respons om hur man kan hantera ett sådant här problem uppskattas :)
Har du ritat området? Det är alltid viktigast.
Du kan använda polära koordinater. Du vet att . Ritar du så ser du att vinkeln du vill integrera från är till (av symmetri) . Du får då integralen:
.
Problemet här är att du måste hantera argument som , det kan vara lite klurigt. (Dock inte så svårt) Så det är inte möjligtvis bättre. Det allra viktigaste är att rita området och förstå vad det är du integrerar.
Tips: och
woozah skrev :Har du ritat området? Det är alltid viktigast.
Du kan använda polära koordinater. Du vet att . Ritar du så ser du att vinkeln du vill integrera från är till (av symmetri) . Du får då integralen:
.
Problemet här är att du måste hantera argument som , det kan vara lite klurigt. (Dock inte så svårt) Så det är inte möjligtvis bättre. Det allra viktigaste är att rita området och förstå vad det är du integrerar.
Tips: och
Yes jag har ritat området, i bilden nedan så är det det röd-blåa området och skär cirkeln i respektive . 
Hmm okej, jag förstår att vi ska (bör) byta till polära koordinater men jag har aldrig gjort det innan där vi inte får någon standardvinkel att jobba med. Sen så är mina trigonometriska färdigheter lite rostiga så du får gärna förklara hur du fick att vinkeln skulle variera mellan och . Åtminstone vart fick du ifrån?
kandersson skrev :woozah skrev :Har du ritat området? Det är alltid viktigast.
Du kan använda polära koordinater. Du vet att . Ritar du så ser du att vinkeln du vill integrera från är till (av symmetri) . Du får då integralen:
.
Problemet här är att du måste hantera argument som , det kan vara lite klurigt. (Dock inte så svårt) Så det är inte möjligtvis bättre. Det allra viktigaste är att rita området och förstå vad det är du integrerar.
Tips: och
Yes jag har ritat området, i bilden nedan så är det det röd-blåa området och skär cirkeln i respektive .
Hmm okej, jag förstår att vi ska (bör) byta till polära koordinater men jag har aldrig gjort det innan där vi inte får någon standardvinkel att jobba med. Sen så är mina trigonometriska färdigheter lite rostiga så du får gärna förklara hur du fick att vinkeln skulle variera mellan och . Åtminstone vart fick du ifrån?
Helt korrekt.
Om du använder så får du att är l.e. och är l.e. Vinkeln mellan dessa är då , eftersom så får du att .
Och du vet att vinkeln du bör dra bort (d.v.s. integrera till) är $\piError converting from LaTeX to MathMLarctan(\theta)$$.
Skriver en ny post eftersom dom fortfarande inte lyckats få skit-redigera att fungera. Sidan laggar lika mycket som Crysis 3 på max på en dator från 1994.
Jag menar i posten ovan , inte .
Du vet att du måste integrera från eftersom du sett från positiva x-axeln har en negativ vinkel. Du ska sedan integrera 180 grader då det är en linje. Då vet du att om du integrerar från så måste den vinkeln du integrerar till vara .
Det viktiga är att mitt sätt fungerar lika bra som ditt. Varför du måste dela upp din integral i två delar är för att om du tittar i positiva x-området så har du inte en längre en entydig funktion. Du måste därför dela upp den i y>0 och y<0. Annars skulle du ha en funktion där du antar både positiva och negativa y-värden för ett enda x-värde (och det går inte för en funktion).
Tack för svaren! Blev lite tydligare nu :)

