3
svar
49
visningar
kandersson är nöjd med hjälpen
Dubbelintegral
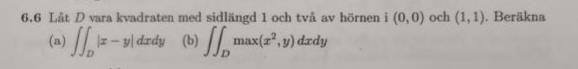
Uppgift (b), jag förstår inte vad de menar med max(x^2,y) i integralen. Hur ska jag tolka det och hur ska det integreras?
Tack på förhand :)
I varje punkt så betyder det största av värdena och . Dvs dela upp i två delområden, ett där är störst och ett där är störst. Analysera t ex olikheten eller kurvan .
Tack! Löste uppgiften :)
Hej!
Det gäller att är samma sak som om punkten är sådan att
Om punkten är sådan att så är För att ta reda på integrationsområdet , rita upp kvadraten som "balanserar på sin spets" och rita in parabeln
Över området ovanför parabeln ska du integrera funktionen och över området under parabeln ska du integrera funktionen
Albiki

