4
svar
92
visningar
1hk1 är nöjd med hjälpen
Dubbelintegral (x^2(ln(x^2+y^2))
Hej!
jag behöver hjälp med uppgiften:
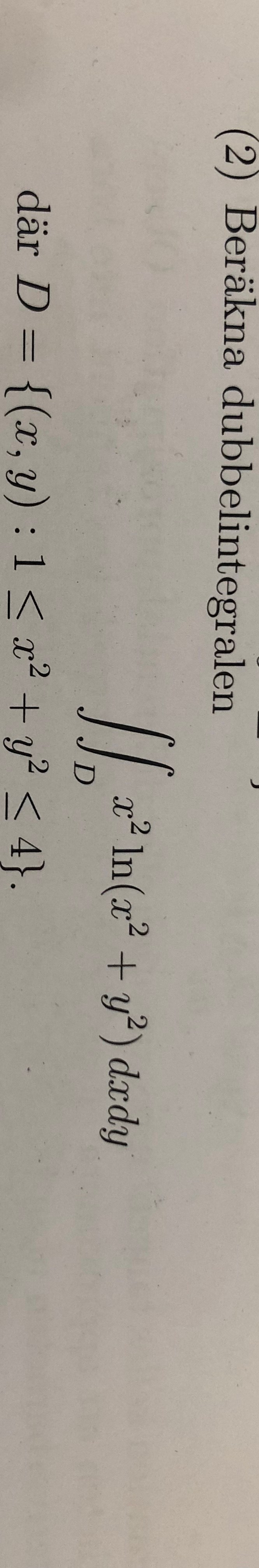
Har du provat med polära koordinater:
Ja, det här är mina uträkningar som blir fel: 
Tyvärr har det blivit rätt så mycket galet i din beräkning.
- Du har slarvat till dina integrationsgränser på första raden (men i och för sig rättat till dem på andra raden). Det skall vara
- Din integrationsordning har blivit fel. Det skall vara istället för eftersom är gränserna tillhörande .
- Du har gjort något väldigt konstigt gällande integranden på andra raden. Det ser ut som du försökt använda identiteten , men att det blivit något fel på vägen.
- Man får bara dela på integralerna om den ena integralen beror av en variabel, och den andra av den andra variabeln. Nu har du uttryck som beror av inuti -integralen efter att du delat på dem. Då blir det pannkaka.
1hk1 skrev:Hej!
jag behöver hjälp med uppgiften:
Kan du lägga in bilden på rätt håll? Jag blir så här

när jag försöker läsa din fråga.




