Ekvation med naturlig logaritm

Det går faktiskt inte att skriva om ekvationen så att man får x = ... Men ekvationen är trots det fortfarande lösbar. Man löser den med hjälp av en funktion som kallas Lamberts W-funktion. Här kan du läsa på lite om den om du vill. 

Lamberts W-funktion – Wikipedia

Lamberts W-funktion är definerad som inversen till f(w) = we^w där w är ett komplext tal. Det finns några detaljer som jag inte har full koll på. Funktionen är dock inte 1-1 vilket innebär att den saknar en invers för hela sin definitionsmängd.

Om man skulle lösa ut x hade det sett ut något i stil med det här:

$\ln \left(x\right)=5-x\to e^{\ln \left(x\right)}=e^{5-x}\to x=e^{5-x}\to x=\frac{e^5}{e^x}\to x{e}^x=e^5.$

$x=W\left(e^5\right)\approx 3.69344135896064980432373934570016822083559376519720079284276144906164379086$

Det långa värdet är beräknat med WolframAlpha.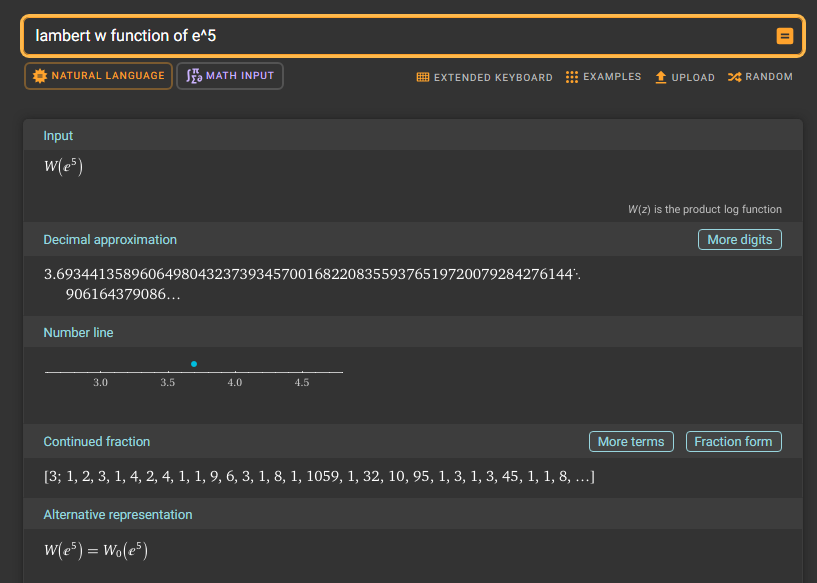

I desmos ser det ut såhär:

Konstigt nog att de skulle ha en sån här uppgift i matte 3, för man verkligen inte behöver kunna det här med Lambert W funktion. Visst, det är bra att veta, men försöker bara säga att det är konstigt att det vore förekomma i denna kurs.

Har de sagt att du skulle använda dig av digitala medlen, som till exempel desmos? Det blir betydligare mycket lättare då.

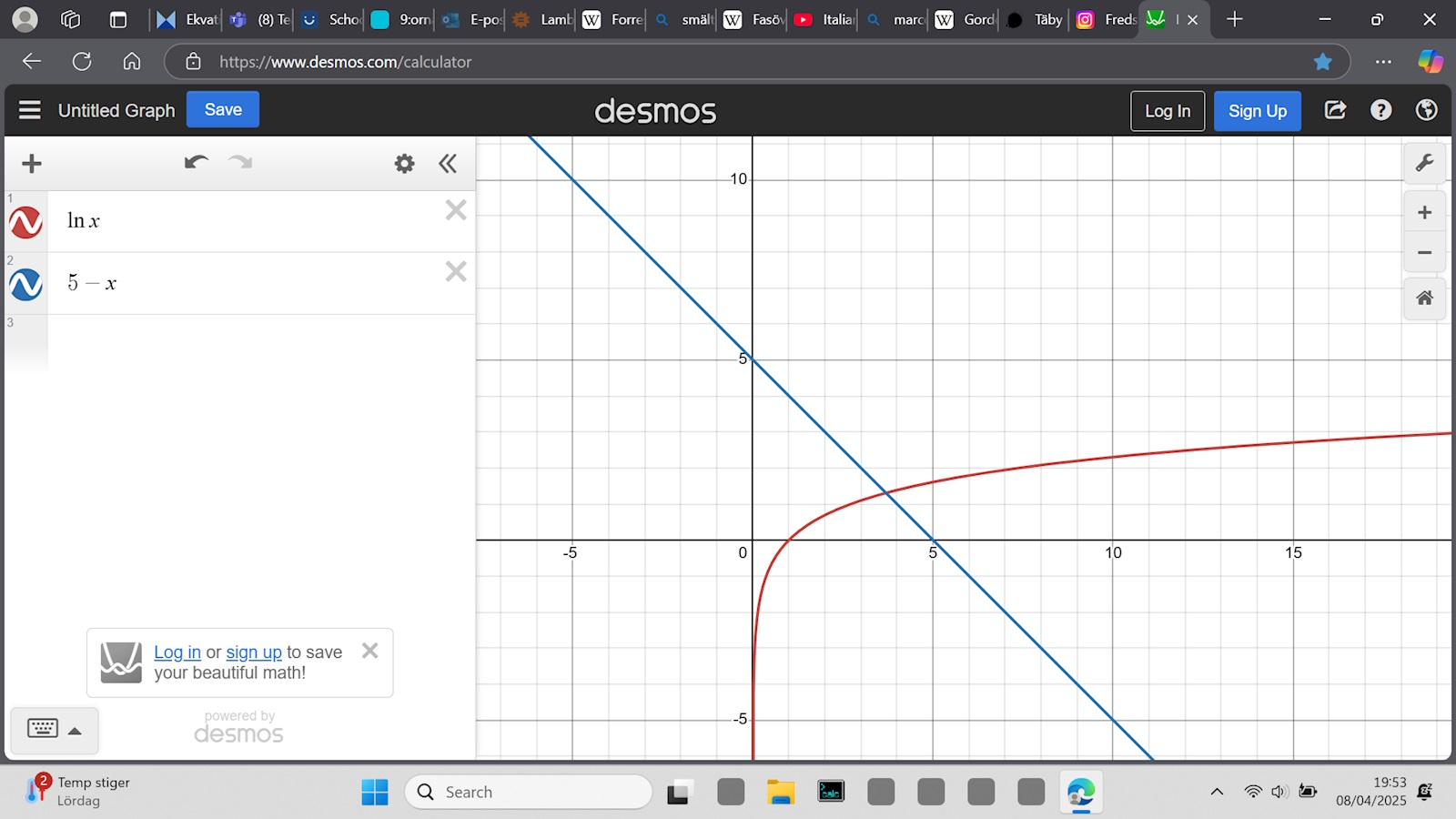
Som du ser så beskriver intersektionen mellan röda linjen och blå linjen då lösningen till ekvationen. Och som Lasse Vegas sa, så blir svaret ungefär att x = 3.693. Ett mer exakt definition av värdet däremot finns bara genom att använda sig av Lambert W funktionen dock.

Jag har tagit denna uppgift från Liber Pyramid av Wallin, Lithner med flera. Tryckt 2001. Kurs C, uppg 4077 s 162.

Det är en uppgift med 2 stjärnor, alltså en svårare utmaning. Enligt bokens framställning har eleverna precis börjat med logaritmerna och inte ens kommit fram till logaritmlagarna. Man ska svara med det bästa närmevärdet med tre decimaler (3,693). Uppgiften är tagen ur CP NT3 1985.