Ekvation som innehåller bråk

Denna ekvation ska lösas utan miniräknare, och jag är osäker på hur jag ska gå till väga...

$\frac{x + 1}{2 x} - \frac{x - 1}{4} = \frac{x + 7}{4}$

Såhär har jag gjort än så länge, men jag vet inte hur jag går vidare i slutet, och om det verkligen är rätt lösning.

$\frac{(x + 1) \times 4}{2 x \times 4} - \frac{(x - 1) \times 2 x}{4 \times 2 x} = \frac{x + 7}{4} \frac{(4 x + 4) - (2 x^{2} - 2 x)}{8 x} = \frac{x + 7}{4} 4 x + 4 - 2 x^{2} + 2 x = \frac{x + 7}{4} \times 8 x 4 \times (6 x + 4 - 2 x^{2}) = 8 x^{2} + 56 x 24 x + 16 - 8 x^{2} = 8 x^{2} + 56 x 16 - 8 x^{2} = 8 x^{2} + 56 x - 24 x 16 = 8 x^{2} + 8 x^{2} + 32 x$

Något magiskt händer i 4:e ledet. Räkna om från 3:e ledet

Trinity skrev:
Något magiskt händer i 4:e ledet. Räkna om från 3:e ledet

Det jag gjorde där var att multiplicera båda leden med 4 för att få bort nämnaren i högerledet. Hur skulle jag gjort istället?

$4 (4 x + 4 - 2 x^{2} + 2 x) = \frac{8 x^{2} + 56 x}{4} \times 4 16 x + 16 - 8 x^{2} + 8 x = 8 x^{2} + 56 24 x + 16 - 8 x^{2} = 8 x^{2} + 56 x$

Jag tror att du räknade rätt från början.

Du fick $16 = 8 x^{2} + 8 x^{2} + 32 x$ . Om du lägger ihop de två $x^{2}$ -termerna och sedan dividerar alla termer med 16 så får du samma ekvation som jag kom fram till.

Sedan är det bara att använda PQ-formeln

Hur får du $8 x^{2}$ i det 4:e ledet?

PluggMotiverad skrev:
Trinity skrev:
Något magiskt händer i 4:e ledet. Räkna om från 3:e ledet

Det jag gjorde där var att multiplicera båda leden med 4 för att få bort nämnaren i högerledet. Hur skulle jag gjort istället?
$4 (4 x + 4 - 2 x^{2} + 2 x) = \frac{8 x^{2} + 56 x}{4} \times 4 16 x + 16 - 8 x^{2} + 8 x = 8 x^{2} + 56 24 x + 16 - 8 x^{2} = 8 x^{2} + 56 x$

Du har inte gjort något fel. Man kan absolut göra som du gjort.

Som jag skriver tidigare, fortsätt nu bara dit du kom första gången och dividera med 16 så har du en mycket fin ekvation.

Det jag glömde fråga om, var att kan du använda PQ-formeln? I så fall är det enkelt, men annars får du återkomma med frågor.

Ni gör det lite svårare än vad det egentligen är

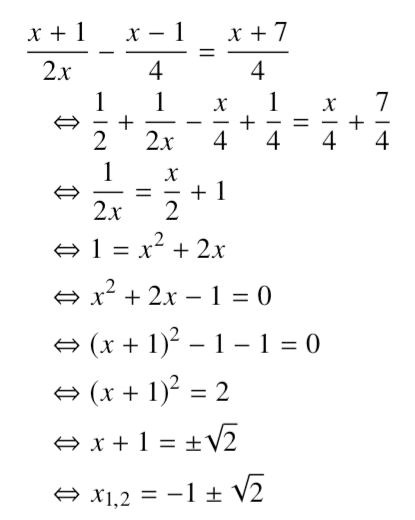
Trinity skriver: Ni gör det lite svårare än vad det egentligen är

Problemet som jag såg, var att du och Iridumjon förvirrade PluggMotiverad

Ni antydde att T.S. gjort fel, men så var det inte.

Du har en galant lösning Trinity. Jag hade också en lite enklare variant, men det viktiga här är att det fanns inga fel i de påbörjade uträkningarna.

Hur använder man pq-formeln? :)

PluggMotiverad skrev:
Hur använder man pq-formeln? :)

Till att börja med, du har inte gjort något fel.

Din uträkning är rätt. Det enda jag vill anmärka på är att du använder "x" som multiplikationstecken, villet kan förvirra eftersom den obekanta storheten också heter x. Använd hellre "•" eller "*".

--------

Du har en andragradsekvation.

Du kommer att lära dig olika metoder att lösa dem i Matte 2. En av dessa metoder kallas pq-formeln.

Är uppgiften verkligen från Matte 1?

PluggMotiverad skrev:
Hur använder man pq-formeln? :)

Om du fortsätter som jag skrev ovan så kommer du till $x^{2} + 2 x - 1 = 0$

Kikar du på Trinitys lösning så ser du att när han kommit så långt så kan du använda hans metod och behöver inte PQ-formeln.

För att komma dit så ser du att första kvadreringsregeln skulle nästan gå att använda $(x + 1)^{2}$ men för att komma dit så behöver du addera 1 till bägge sidor två gånger och då har du $x^{2} + 2 x + 1 = 2$ och då kan du kanske förstå Trinitys avslut?

Ojdå jag såg på din profilsida att du går i nian, men är du intresserad så hittade jag en fin video på mattecentrum som förklarar PQ-formeln så jag tror att du kan ta till dig den?

https://www.youtube.com/watch?v=T1iZIAML5CI

Den är kort. Lycka till :-)

Tack för all hjälp!

Jag går första året på gymnasiet nu, hade bara glömt att uppdatera min profil. :)

Svara

Visa senaste svar