Ekvationssystem varför ger en liten ändring en stor förändring
Hej!
Ekvationssystem:
ax+ 12y = 11
69x + 25y = 27
lös det med a =33 och sedan a = 33.1
Förklara geometriskt varför en liten ändring av koefficienten a ger en stor förändring i lösningen.
a = 33
x = 49/3
y = -44
a = 33.1
x = 98
y=-269.4
Jag kan inte förklara varför. Eller jag förstår inte varför heller för den delen.
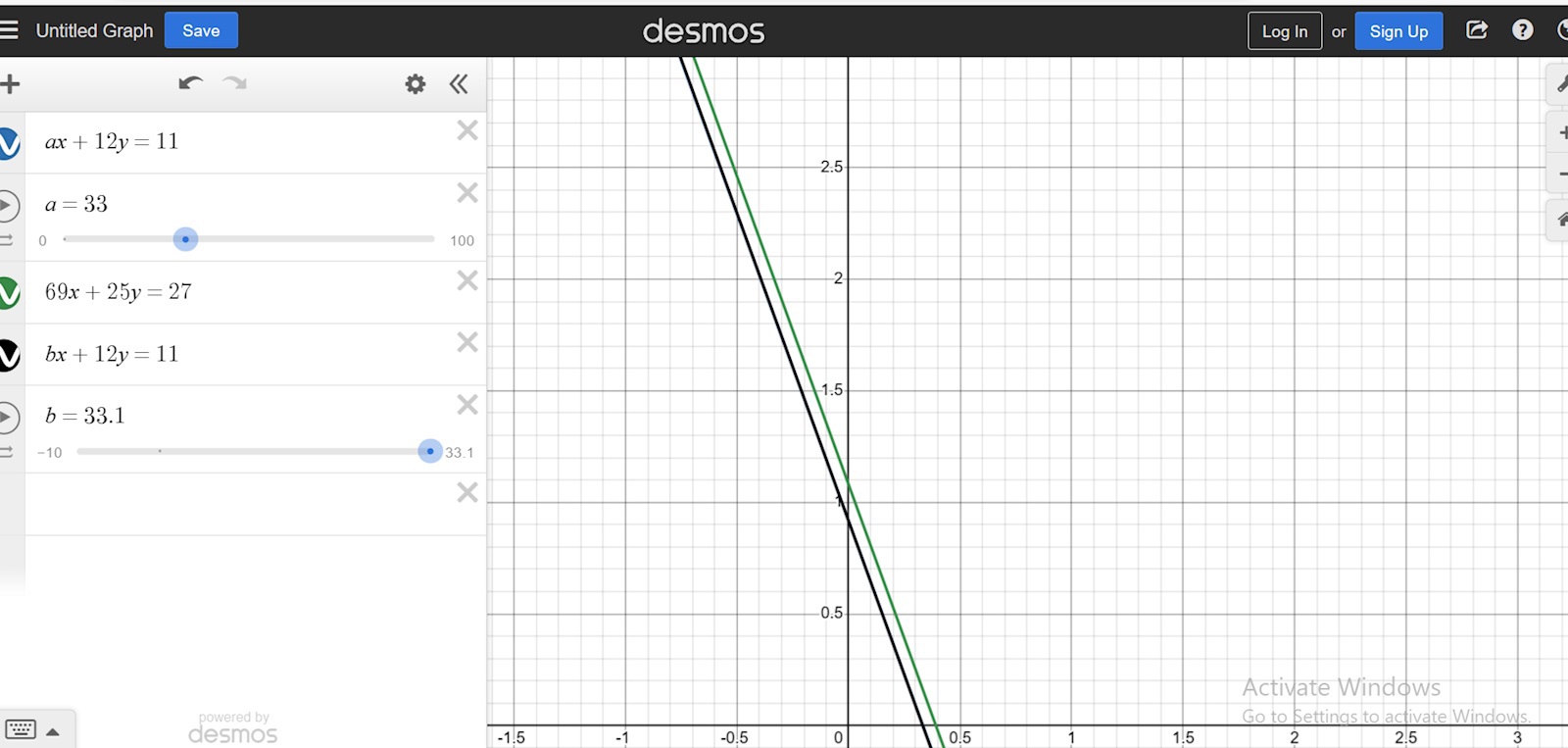
Jag har ritat upp dem i Desmos och ser att linjerna nästan är parallella.
Visa din Desmosritning så går vi vidare från den.
Vid a = 33.1 så lutar linjen något mer emot den gröna, det betyder att dom borde skära varandra tidigare, inte senare. Men så är inte fallet...
Dkcre skrev:Vid a = 33.1 så lutar linjen något mer emot den gröna, det betyder att dom borde skära varandra tidigare, inte senare. Men så är inte fallet...
Om du skriver ekvationerna på standardformat y = kx+m så ser du att om a = 33 så blir k = -33/12 och om a = 33,1 så blir k = -33,1/12.
Det betyder att linjen lutar mindre mot den gröna när a = 33,1
Okej, ja då är jag helt med. Men varför måste man skriva om ekvationerna.
Eller det ingår väl i uppgiften att man ska vara med på att man måste göra så för att de ska kunna representeras som räta linjer, naturligtvis.
Man kan säkert lära sig att se hur linjer lutar även om de är skrivna på formen ax+by = c, men för mig är det enklare att skriva om den.
Edit:
Ursäkta, jag är trött. Fixade till det.
Tack så mycket för hjälpen!
Dkcre skrev:Men varför måste man skriva om ekvationerna.
Det måste man inte. Men det blev enklare att se lutningen då.
[...] att man måste göra så för att de ska kunna representeras som räta linjer, naturligtvis.
Nej, det behövs inte.
Ekvationen ax+by = c är en generell representation av en rät linje (som dessutom hanterar vertikala linjer, vilket inte y = kx+m gör).
Jag förstår inte riktigt varför det blir lättare, den lutar väl som den gör i vilket fall..
Ja, men om linjen är skriven på formen y = kx+m så vet jag att k är lutningen. Det kan jag inte se lika enkelt för linjen ax+by = c. Jag skulle kunna lära mig det, men jag tycker det är enklare att skiva om linjen på det sätt jag föredrar.
Okej. Förstår. Ser i Desmos här att om jag skriver den på generella formen så vrider den sig mer mot den gröna linjen när värdet på a ökar, inte tvärtom. Tycker det är lite märkligt.
Dkcre skrev:Okej. Förstår. Ser i Desmos här att om jag skriver den på generella formen så vrider den sig mer mot den gröna linjen när värdet på a ökar, inte tvärtom. Tycker det är lite märkligt.
Linjens ekvation kan skrivas
Är du med på att om ökar så vrider sig linjen medurs, dvs den lutar brantare neråt?
Tillägg: 11 apr 2024 10:03
Missade ett x i ekvationen.
Det ska vara .
Tack Smaragdalena.