Elektriska kretsar - hur fungerar ett filter av denna typ av AC-krets?

Halloj!

Jag håller på att kolla på frågor från gamla duggor och studerar nu exemplet nedan

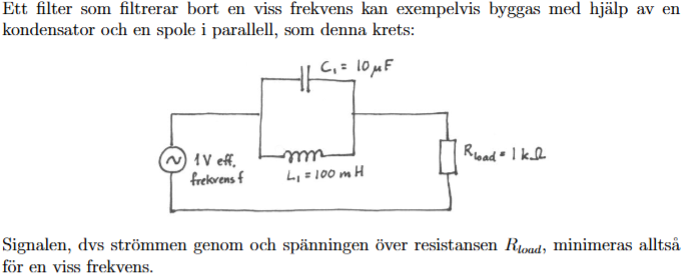
Jag är inte riktigt med på hur detta fungerar. Jag antar att man tänker att spänningskällan alstrar en spänning som kan anses vara en summa av sinusoidala och kosinusoidala kurvor. Varje sådan kurva har då generellt en egenfrekvens $\omega = 2\pi f$ . Så jag antar att då strömmen passerar "filtret" så dör komponenter av vissa (egen)frekvenser ut så att den effektiva signalen inte har dessa komponenter i sig. Men hur funkar det i den här kretsen? Varför dödas vissa delar av insignalen?

Jag tänker att man borde kunna skriva inströmmen som en summa av sinusfunktioner:

$\displaystyle i\left(t\right)=\sum_{k}a_k\sin\left(\omega_kt\right)=\sum_{k}\frac{a_k}{2j}\left(e^{j\omega_kt}-e^{-j\omega_kt}\right)$

Och jag vet också att impedansen för de olika komponenterna ges av $Z_C=(j\omega C)^{-1}$ , $Z_L=j\omega L$ samt $Z_R=R$ .

EDIT:

Jaha, jag tror jag fattar nu. Ersättningsimpedansen över LC-parallellkopplingen kan skrivas

$\displaystyle Z_{\text{ers.}}\left(\omega\right)=\frac{Z_CZ_L}{Z_C+Z_L}$

Då måste det ju vara så att vid $\omega = \frac{1}{\sqrt{LC}}$ så har vi "oändlig impedans" över filtret och då kan det inte gå någon ström för den egenfrekvensen. Stämmer det?

Precis! Men i verkligheten finns ingen spole eller kondensator som är helt ideal. Det finns resistiva förluster i båda. Det finns små små kapacitanser mellan lindningarna som gör att spolen ser ut som en kapacitans vid mycket höga frekvenser, etc. Det gör att LC-nätet impedans aldrig blir oändlig.

Eftersom dämpningen för varje frekvens beror på spänningsdelningen mellan lastens R och filtrets impedans så är det när filtrets impedans börjar få samma storleksordning som lasten, som det händer mest saker

Vid låga frekvenser är X_L liten.
Vid höga frekvenser är X_C liten.
I dessa båda fall beror strömmen i stort sett bara på spänningskällan och resistansen.

Någonstans däremellan är X_Loch X_C inte försumbara.

Om man låter frekvensen svepa får man en karakteristik som ser ut ungefär så här:

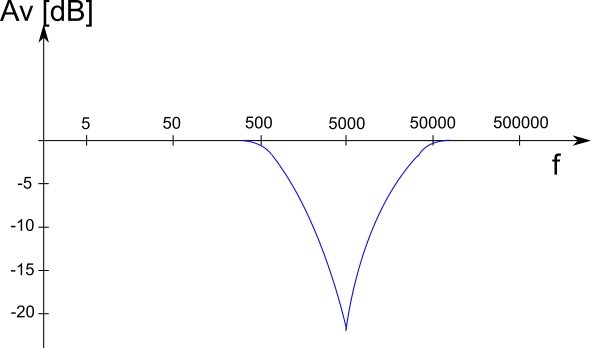
Obs, siffrorna på axlarna stämmer troligen inte med de komponentvärden du har.

ThomasN skrev:
Vid låga frekvenser är X_L liten.
Vid höga frekvenser är X_C liten.
I dessa båda fall beror strömmen i stort sett bara på spänningskällan och resistansen.

Någonstans däremellan är X_Loch X_C inte försumbara.

Om man låter frekvensen svepa får man en karakteristik som ser ut ungefär så här:

Obs, siffrorna på axlarna stämmer troligen inte med de komponentvärden du har.

Vad betecknar X?

X_L är impedansen i spolen, jwL. X_C är impedansen i kondensatorn, 1/jwC. Båda är frekvensberoende.

I diagrammet är horisontella axeln frekvensen på växelströmskällan. Skalan är logaritmisk.
På vertikala axeln har vi förhållandet mellan in- och utsigal, 20log(Uut/Uin).

Hej, igen.

Jag sitter med den här uppgiften återigen och jag vill bara bekräfta att jag förstår vad som händer här. Vi har att kretsens komplexa impedans ges av uttrycket nedan, där strecket över symbolerna innebär att talet är komplext:

$\displaystyle \bar{Z}=R_{\text{load}}+j\left(\frac{\omega L_1}{1-\omega^2C_1L_1}\right)$

Enligt Ohms generaliserade lag har vi då alltså:

$\displaystyle \bar{I}=\frac{\bar{U}}{R_{\text{load}}+j\left(\frac{\omega L_1}{1-\omega^2C_1L_1}\right)}$

Om vi skriver den komplexa impedansen, den komplexa spänningen och den komplexa strömmen på polär form, där vi väljer att ge spänningen fasförskjutning noll, har vi:

$\displaystyle \left(I_{\text{eff.}}\sqrt{2}\right)e^{j(\omega t-\varphi)}=\frac{U_0e^{j\omega t}}{e^{j\varphi}\sqrt{R_{\text{load}}^2+\left(\frac{\omega L_1}{1-\omega^2C_1L_1}\right)^2}}$

Efter lite omskrivning får vi:

$\displaystyle I_{\text{eff.}}\left(\omega\right)=\frac{U_{\text{eff.}}}{\sqrt{R_{\text{load}}^2+\left(\frac{\omega L_1}{1-\omega^2C_1L_1}\right)^2}}$

Ju större nämnaren i HL blir, desto mindre blir strömmens effektivvärde. I gränslandet där nämnaren är "oändligt stor" blir strömmen "oändligt liten". Detta uppnås då $\omega=\omega_0=1/\sqrt{L_1C_1}$ .

Är det korrekt resonerat?

Håller helt med

Håller också med.

Okej, tack! :)

Svara

Visa senaste svar