Elektriska kretsar - varför räknar föreläsaren med beloppet av impedansen?
Hej!
Jag studerar exempelfrågan nedan:

Jag har två frågor om denna fråga. Den första är: vad menas ens med huruvida strömmen är störst eller minst vid den frekvensen? Det är ju en växelström så hur mycket ström som går genom kretsen varierar väl med tiden?
Jag tänkte först naivt att man kunde studera (eftersom det specificeras att kurvan är en sinuskurva) men i facit har man valt att räkna med kretsens impedans. Man har gjort så här:
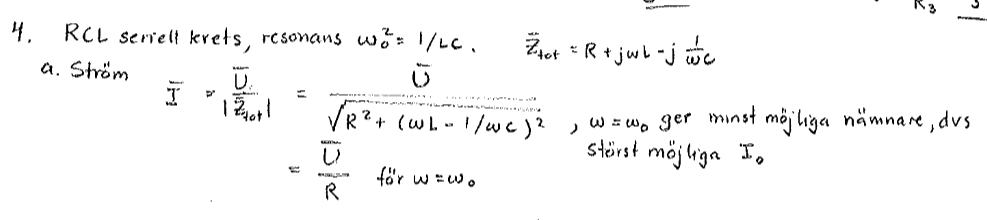
Men vad är det som händer här? Varför tar man beloppet av kretsens impedans? Och även om vi räknar så, hur kan tentamakaren inordna någon slags "storlek"? Den komplexa strömmen har ju ingen storlek.
Hej!
Man menar storleken på effektivvärdet av strömmen. Den blir störst eller minst när kretsens impedans är som minst eller störst, eftersom källan är en spänningskälla och därmed ger konstant spänning över RLC-kretsen. Alltså är det lämpligt att titta på utseendet på RLC-kretsens impedans.
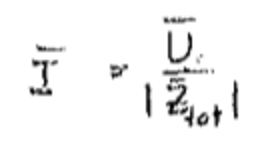
Men hur kan impedansen vara större eller mindre? Impedansen är väl ett komplext tal?
Jag tänkte just förklara, för jag kom på att detta inte var självklart för dig.
Ja, kretsens impedans är komplex, dvs den kommer att fasvrida strömmen relativt spänningen. Dvs det hade gått bra att analysera kretsen på det sätt du gjorde ansats till också, men du hade landat i precis samma slutsats som facit, men på ett lite jobbigare sätt. Eftersom det inte var kretsens fasvridande egenskaper uppgiften frågade efter, utan bara hur effektivvärdet på strömmen betedde sig, så hade facit en enklare lösningsstrategi.
I resonans är dessutom impedansen inte komplex, eftersom de reaktiva delarna kancellerar varandra. Det är detta som gör att impedansen över en sådan krets är större eller mindre, beroende på strömmens frekvens.
Jag tror att jag hänger med, men vi får se. Jag ursäktar för att jag är så förvirrad; jag har varit sjuk en del och kurskompendiet är långt ifrån trivialt (och det är fortfarande ingen tillbaka på hjärnkontoret...).
Om jag har förstått det rätt kan man räkna med att den komplexa strömmen, låt oss kalla den , ges av för en ström . Realdelen av ger då . Stämmer det?
Ja, ungefär. Det är det som är -metoden. En riktigare förklaring är att du vet att spänningen är en sinusfunktion. Då kan du beteckna den som realdelen (eller imaginärdelen) av .
Du kan sedan teckna den komplexa impedansen på exponentialform, varefter räkna ut genom att använda logaritmlagar för division, och slutligen ta realdelen (eller imaginärdelen) av för att få ett uttryck för den verkliga strömmen. Inklusive amplitud och fasvridning relativt spänningen.
Om vi har att , har vi då automatiskt i allmänhet där är kretsens sammanlagda fasförskjutning?
Ja. I den här uppgiften är spänningen "känd", och man söker strömmen. Då är det naturligt att låta spänningen vara riktfas, dvs ge den fasvinkel 0 grader. Och låta fasvridningen phi bli ett uttryck i strömmen.
För att återkoppla till din ursprungliga uppgift så ser du kanske nu varför facit bara räknar på impedansens absolutbelopp. Man är helt enkelt inte intresserad av eventuell fasvinkel.
Okej, så vi har samt .
Jag tolkar det som att vi kan välja om vi vill ge spänningen eller strömmen fasförskjutningen; vi kan "flytta" hela koordinatsystemet så att en av dem blir en vanlig sinuskurva.
Vi har då alltså och likaså , visst?
Jag är fortfarande inte riktigt med på varför man tar beloppet av impedansen. Om jag har förstått det hela rätt kan vi ställa upp:
Här kan vi få ett uttryck för som är tidsoberoende, vilket verkar lovande.
Jag håller med om allt du skriver.
Eftersom du kan skriva den komplexa impedansen på exponentialform som
Absolutbelopp*e^(j*phi)
så ser du att det är bara absolutbeloppet av impedansen som påverkar effektivvärdet av strömmen.
Ah, nu tror jag att jag är med! Fasförskjutningen är samma vinkel som finns mellan impedansens resistiva och reaktiva del, eller hur? Får vi då alltså uttrycket nedan?
Men har man inte kvar en imaginärdel i det här uttrycket?
Tillägg: 23 nov 2025 21:42
ChatGPT menar att impedansen bör ha vinkel men detta förstår jag inte riktigt. Jag hade fått för mig att de är samma. Har det att göra med om man väljer ström- eller spänningsfasorn som referens (vinkel noll)? Jag tror att vår föreläsare gav strömmen fasvinkel noll.
Ah, nu tror jag att jag är med! Fasförskjutningen φ är samma vinkel som finns mellan impedansens resistiva och reaktiva del, eller hur?
Precis!
Du har och du kan teckna impedansen på exponentiell form som
Du kan då beräkna
Alltså är det enda intressanta för uppgiften, absolutbeloppet av impedansen.
Jag tror att chatgpt har lite svårt att förklara på ett stringent sett här. En komplex impedans har en fasvridande komponent . Huruvida blir positiv eller negativ i uttrycket för ström och spänning följer direkt ur ohms lag och logaritmreglerna. Spänningen fås genom att _multiplicera_ impedansen med strömmen, alltså _addera_ i exponenten. Strömmen fås genom att _dividera_ spänningen med impedansen, alltså _subtrahera_ φ i exponenten. Det centrala är att oavsett om adderas eller subtraheras, så blir _fasskillnaden_ mellan ström och spänning densamma. Om impedansen är induktiv så kommer spänningen att komma före strömmen i tiden, och om impedansen är kapacitiv så kommer strömmen att komma före spänningen i tiden.
Din föreläsare kommer definitivt att välja vem som ska ha vara riktfas beroende på hur uppgiften ser ut. Antag att din föreläsare förevisar hur man skulle kunna lösa uppgiften ovan med tillägget att man också ska teckna ett uttryck för strömmen. Det hade varit väldigt ointuitivt att först ansätta en spänning och sedan räkna fram ett uttryck för strömmen . säger ju ingenting om fasskillnaden mellan spänning och ström om man inte samtidigt anger . Alltså, man väljer alltid riktfas som det som är intuitivt enklast (eller om det anges i uppgiften).
(Jag måste erkänna att jag inte riktigt vet vad din föreläsare menar med U-tak och I-tak i just det här fallet. Kanske är det en konventionell definition av effektivvärde eller toppvärde? Annars kommer det här sambandet som hen skrev inte att gälla
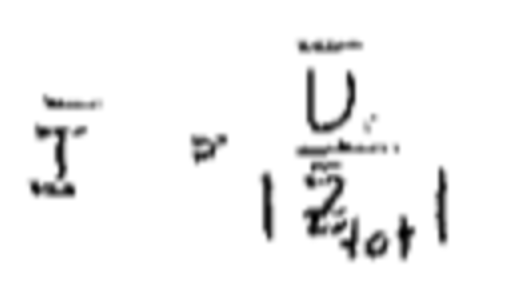
Tak betyder att det är komplext snarare än reellt i hennes symbolkonvention.
Jag förstår ditt uttryck för strömmen, men vi vill ju ha strömmens effektivvärde. Då jag försöker räkna ut detta ställer jag upp ekvationen:
Problemet är ju att vid division blir vi inte av med utan vi får istället om jag tänker rätt.
Jag tror att vår föreläsare har sagt att vi "bestämmer" att strömmen alltid har fasförskjutning 0. Om man räknar så och ger fasförskjutningen till spänningen istället, så att vi har , så blir det ju rätt.
Då måste hon ha slarvat med det formella i facit. Om U-tak och I-tak är de komplexa uttrycken för strömmen och spänningen i det generella fallet så kan inte sambandet mellan dem beskrivas med en reell konstant. Vi har ju just lärt oss att det finns en fasskillnad mellan strömmen och spänningen eftersom impedansen är komplex. Utom just i resonansen, då impedansen är reell.
Eller vad tycker du?
Jag håller med och det var därför jag var så förvirrad kring facit; det mejkade ingen sense med våra symbolkonventioner. Det kan hända att hon helt enkelt slarvade eller skrev fel av misstag.
Men om vi återgår till uppgiften, håller du med om ekvationen jag skrev upp i #13? Det är meningen att det ska komma från generaliserade Ohms lag . I så fall förstår jag fortfarande inte riktigt hur man ska hantera problemet vi stöter på med att vi får i nämnaren istället för att vi blir av med .
Som sagt nämnde min föreläsare någon gång att vi alltid bestämmer att strömmen är storheten utan fasförskjutning och att spänningen får eventuell fasförskjutning. Om man räknar med försvinner väl problemet?
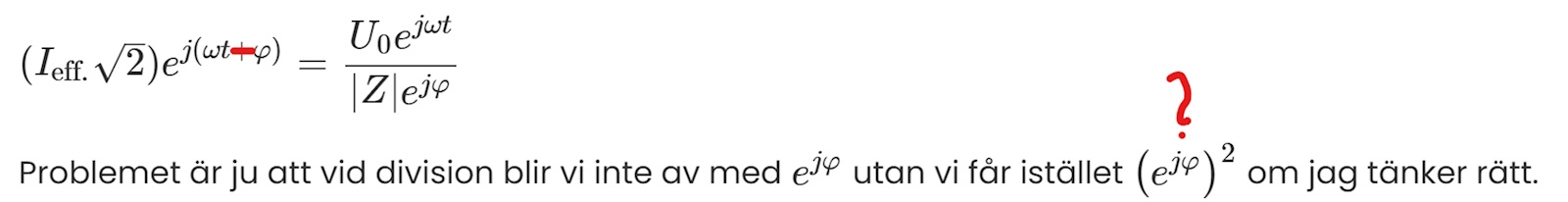
Det blir minus i vänsterledet. Potenslagarna är dessa 
Var får du 2'an ifrån?
(inser nu att jag skrivit logaritmlagar i hastigheten på något ställe här ovanför)
![]()
Vad är detta för fråga?
(Man lägger sitt koordinatsystem som det passar bäst, precis som när man jobbar med andra typper av koordinatsystem)
Hoppsan, jag menade ”om man räknar med det”.
Varför ska det vara minus fasförskjutningen i strömmen? Tvåan uppkom av att räkna med i strömmen.
Tillägg: 24 nov 2025 10:00
Antag att vi ansätter:
där är fasförskjutningen. Om vi ställer upp generaliserade Ohms lag och jämför exponential- och faktordel får vi .
Är det alltså korrekt att om spänningen har referensvinkel noll får strömmen fasvinkel . Om strömmen har referensvinkel noll får spänningen referensvinkel ?
Är det alltså korrekt att om spänningen har referensvinkel noll får strömmen fasvinkel −φ. Om strömmen har referensvinkel noll får spänningen referensvinkel +φ?
Ja, det är korrekt. Det centrala är att oavsett val av koordinatsystem så ligger spänningen före strömmen om den komplexa impedansen har induktiv komponent (dvs om impedansens fas phi är positiv). Och spänningen ligger efter strömmen om den komplexa impedansen har kapacitiv komponent (dvs om impedansens fas phi är negativ)
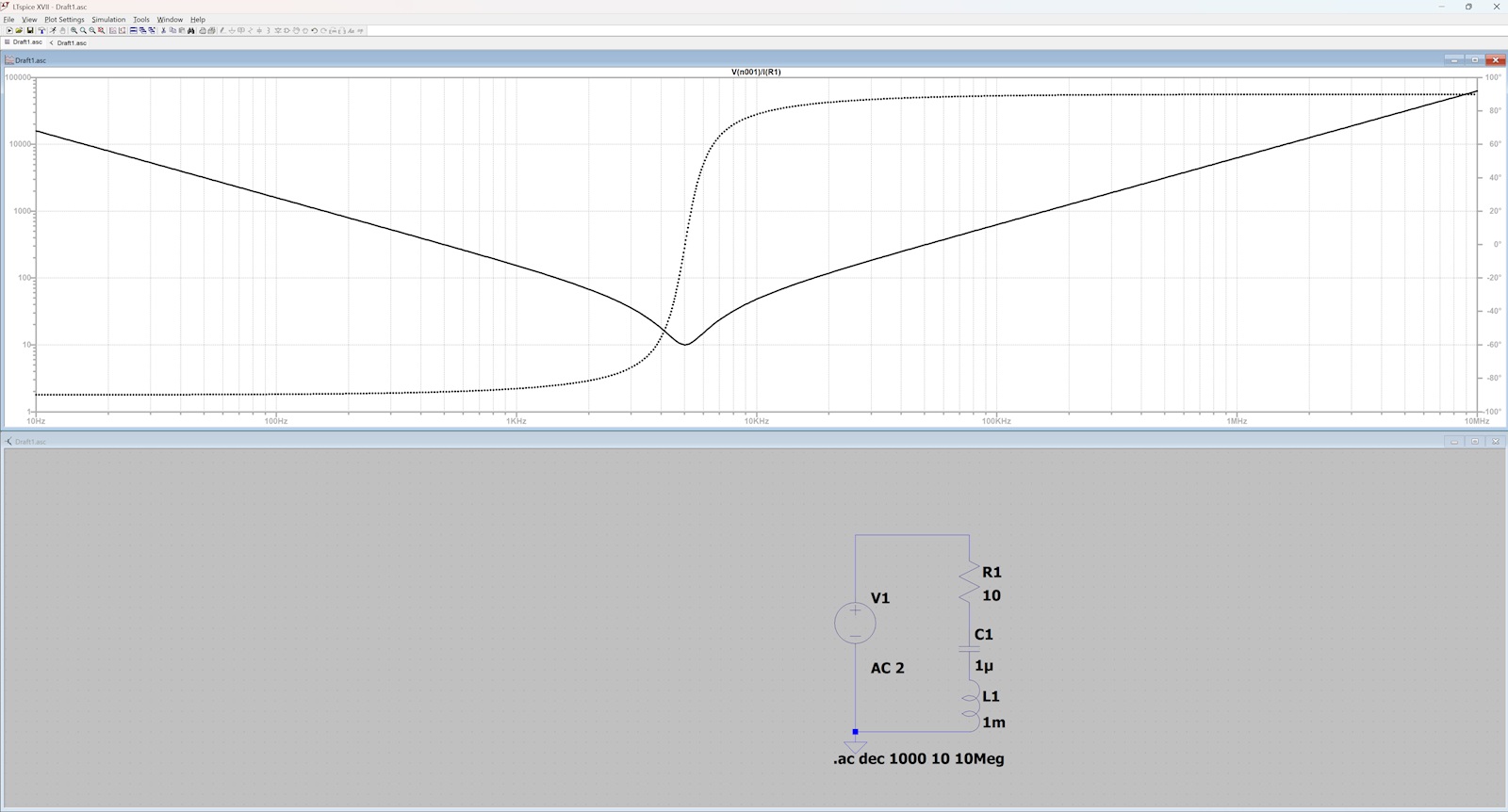
Och huruvida impedansen har en induktiv eller kapacitiv kapacitiv komponent beror på frekvensen samt värden på komponenterna, eller hur?
Exactly! Om man tar RLC-kretsen som exempel. Vid "låga" frekvenser så är kretsens impedans kapacitiv (intuitivt enkelt att tänka sig, eftersom kapacitansen blockar DC). Vid "höga" frekvenser är kretsen induktiv (intuitivt enkelt att tänka sig då en kapacitans i stort sett ser ut som en kortslutning vid mycket höga frekvenser). Vid resonans, när de två reaktiva komponenterna tar ut varandra är RLC-kretsen rent resistiv, dvs har ingen fasvridande effekt alls.
Vad som är "hög" respektive "låg" frekvens, bestäms av de ingående komponentvärdena.
Jag gjorde en snabb simulering av RLC-kretsens impedans för några "normala" värden på komponenterna (ofta plottar man med log-log-skala för att kunna visualisera beteendet bättre då dynamiken är så stor). Den streckade kurvan är fasen, som kan läsas på den högra y-axeln
Impedansen fasvrider så att strömmen kommer 90grader före spänningen vid låga frekvenser, och kommer 90grader efter spänningen vid höga frekvenser.