En annorlunda andragradsekvation

Det löner sig alltid att skissa. Grejen är symmetrisk.

$\sqrt{5-x}= 5-x^2 \implies x=\pm \sqrt{5- \sqrt{5-x}}$, Notera vad som händer om vi tar den positiva varianten och stoppar in x, vi får då ett rekursivt problem m.a.p $\sqrt{5}$, detta ger direkt att $x=\sqrt{5-x}$ som vi kan skriva om till $x^2+x-5$. Notera att om vi hade kvadrerat istället så hade vi kommit fram till $x^4-10x^2+x+20=0$, poldiv ger ny att $(x^2+x-5)(x^2-x-4)=0$ och lösningarna ges av (efter vi förkastat de falska rötterna) $x_1=\dfrac{-1+ \sqrt{21}}{2}, x_2=\dfrac{1- \sqrt{17}}{2}$.

Första roten kan man hitta alternativt med hjälp av symmetri:

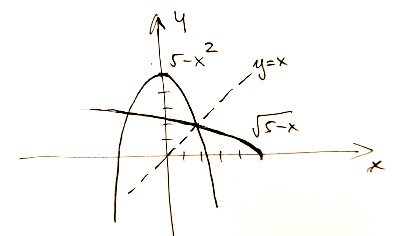
5 - x² = x

Man kan också tänka så här. (Samma idé som Macilaci.)

Hitta skärningen mellan kurvorna:

$$\begin{gathered} y=\sqrt{5-x} \mathrm{och} y=5-x^2 \Rightarrow \\ {y}^2=5-x \left(1\right) \\ y=5-x^2 \left(2\right) \\ \left(1\right)-\left(2\right) \\ {y}^2-y=x^2-x \\ y(y-1)=x(x-1) \\ \mathrm{En} \mathrm{lösning} \mathrm{är} \mathrm{uppenbarligen} y=x \Rightarrow \\ x=\sqrt{5-x}\Rightarrow \\ {x}^2+x-5=0 \\ \mathrm{osv} \end{gathered}$$

Nyfiken på den utlovade spoilern ...

Notera att ekvationen $\sqrt{6-x}=5-x^2$är svårare men eftersom det blir en fjärdegradsekvation ska den vara möjlig att lösa exakt. Jag kommer dock inte ge mig på det ...

henrikus skrev:

Man kan också tänka så här. (Samma idé som Macilaci.)

Hitta skärningen mellan kurvorna:

$$\begin{gathered} y=\sqrt{5-x} \mathrm{och} y=5-x^2 \Rightarrow \\ {y}^2=5-x \left(1\right) \\ y=5-x^2 \left(2\right) \\ \left(1\right)-\left(2\right) \\ {y}^2-y=x^2-x \\ y(y-1)=x(x-1) \\ \mathrm{En} \mathrm{lösning} \mathrm{är} \mathrm{uppenbarligen} y=x \Rightarrow \\ x=\sqrt{5-x}\Rightarrow \\ {x}^2+x-5=0 \\ \mathrm{osv} \end{gathered}$$

Nyfiken på den utlovade spoilern ...

Notera att ekvationen $\sqrt{6-x}=5-x^2$är svårare men eftersom det blir en fjärdegradsekvation ska den vara möjlig att lösa exakt. Jag kommer dock inte ge mig på det ...

 När man hittat lösningen y=x är det lätt att faktorisera

 $$\begin{gathered} y^2-y-x^2+x=(y-x)(y+x-1)=0 \\ Den andra lösningen är y=1-x\Rightarrow \\ 1-x=\sqrt{5-x}\Rightarrow \\ {x}^2-x-4=0 \\ osv \end{gathered}$$

Alla har gett mycket intressanta svar och jag tycker att alla har gett ganska intressanta synvinklar på det. Den första lösningen är lik Dracaena's lösning där man får 

$x=\mp \sqrt{5-\sqrt{5-x}}$

Vi får därför 2st olika lösningar. 

$x=\sqrt{5-x}$ och $x=-\sqrt{5-\sqrt{5+\sqrt{5-\sqrt{5-x}}}}$

Den första löses på samma sätt som Dracaena förslog och det andra följer en formel för alternerande oändligt kapslade radikaler. 

 

$\sqrt{a-\sqrt{a+\sqrt{a-\sqrt{a}}}}...=\frac{\sqrt{4a-3}-1}{2}$

då får man $x=-\frac{\sqrt{20-3}-1}{2} \to x=\frac{1-\sqrt{17}}{2}$

 

Den andra lösningen är den jag själv tycker mest om dock. Denna innebär att man ska göra det som man oftast rekommenderas att inte göra i detta fallet. Att kvadrera båda sidorna.

Detta betyder att

$5-x=5^2-2(5·x^2)+x^4 \to 5^2+(-2x^2-1)·5+x^4+x=0$

Nu har jag skrivit det lite konstigt kan man tycka men det är med meningen. Det vi nu har är en andragradsekvation inom 5 och inte inom x. Använder vi nu oss av pq formeln så kan vi enkelt lösa ut x

$5=-\frac{-2x^2-1}{2}\mp \sqrt{{\left(\frac{-2x^2-1}{2}\right)}^2-(x^4+x)}$

Förkortning ger

$5=x^2+\frac{1}{2}\mp \sqrt{x^2-x+\frac{1}{4} }\to 5=x^2+\frac{1}{2}\mp \sqrt{{(x-\frac{1}{2})}^2}$

 

Detta betyder sen att vi får två stycken andragradsekvationer

$5=x^2+x$

$5=x^2-x+1$

och sedan löses dessa på samma vis 

man kommer alltså här fram till 4 st lösningar men som tidigare nämnts finns bara 2 st.

Detta är för x endast är giltigt om

$-\sqrt{5}\le x\le \sqrt{5}$

Detta låser därför ut 2 av svaren och vi slutar på samma vis med samma lösningar.