En bolls höjd och sträcka, andragradsekvation.
Fråga: Pontus kastar iväg en boll så att dess höjd över marken, h(x), beror av bollens sträcka längst marken, x, enligt:
h(x) = -0,020x^2 + 0,55x + 1, 65. både bollens höjd och dess förflyttning, mäts i meter.
(a) Bestäm bollens höjd då den rört sig 5m längst marken.
(b) bestäm bollens högsta höjd samt hur lång sträcka längst marken som den då har rört sig.
Jag har fått hjärnsläpp på denna uppgift totalt. På fråga A har jag bara satt in 5 ist för X alltså blir ekvationen
-0,5 + 2,75 + 1,65 = 3,9
Jag är inte riktigt säker på om jag fick ut rätt tal på den första alltså att : -0,020x^2 = -0,5. Men annars så är jag rätt säker på att helheten är rätt, rätta mig om jag har fel här.
Men till fråga B, jag förstår inte riktigt vad dem frågar efter? Hur jag ska tolka frågan och hur man ska gå till väga för att lösa den uppgiften. Jag erkänner att jag inte riktigt förstår mig på uppgiften och vad alla talen står för i ekvationen. Hur får man ut bollens högsta höjd? och hur lång sträcka den då har rört sig?
Välkommen till Pluggakuten!
Vet du hur man gör när man löser en andragradsekvation? Känner du till begreppet symmetrilinje?
Smaragdalena skrev:Välkommen till Pluggakuten!
Vet du hur man gör när man löser en andragradsekvation? Känner du till begreppet symmetrilinje?
PQ formeln då eller?
hört begreppet symmetrilinje men jag kollar upp det!
Smaragdalena skrev:Välkommen till Pluggakuten!
Vet du hur man gör när man löser en andragradsekvation? Känner du till begreppet symmetrilinje?
Jag skrev ner PQ formeln.
Gjorde jag fråga a rätt? att bara sätta in 5?
Fick fram på b efter jag gjort PQ formeln
x = 13,75 +/- 16,5
x1 = 30,2m x2 = 2,75m
men vet inte vilken som är vilken, vilken är höjden och vilken är förflyttningen liksom? Är detta hela svaret? är lite osäker på vad jag har svarat på if that makes sense?
Ja, du har gjort rätt på a-uppgiften.
På b-uppgiften gäller att symmetrilinjen ligger mitt emellan nollställena, dvs vid x = 13,75.
Bollen når alltså sin högsta höjd då = 13,75 meter.
Kommer du vidare då?
Nästan rätt.
Andra lösningen är inte 2.75m utan -2.75m.
Funktionen h(x) är definierad för alla x, men om man tänker efter är ju inte alla x tillåtna:
Efter ett tag slår bollen i golvet, så x kan inte bli hur stort som helts. Man kastar bollen så att x ökar från noll, så x kan inte vara negativt.
Om man tänker sig att man "förlänger" bollens bana, framåt tills den försvinner ner i ett gruvhål, och bakåt i tiden så att den sedan dyker upp på höjden 1.65 vid tiden noll, ja då har man med fler värden på x. I det här fallet skulle man kunna ha kastat bollen vid x=-2.75m så att den sedan hade följt just den bana som är given.
Yngve skrev:Ja, du har gjort rätt på a-uppgiften.
På b-uppgiften gäller att symmetrilinjen ligger mitt emellan nollställena, dvs vid x = 13,75.
Bollen når alltså sin högsta höjd då = 13,75 meter.
Kommer du vidare då?
Vet inte. Om höjden är 13,75. Vad är då 30,2 för ngt? Är det det som är sträckan? Det är så jag tänker
Bubo skrev:Nästan rätt.
Andra lösningen är inte 2.75m utan -2.75m.
Funktionen h(x) är definierad för alla x, men om man tänker efter är ju inte alla x tillåtna:
Efter ett tag slår bollen i golvet, så x kan inte bli hur stort som helts. Man kastar bollen så att x ökar från noll, så x kan inte vara negativt.
Om man tänker sig att man "förlänger" bollens bana, framåt tills den försvinner ner i ett gruvhål, och bakåt i tiden så att den sedan dyker upp på höjden 1.65 vid tiden noll, ja då har man med fler värden på x. I det här fallet skulle man kunna ha kastat bollen vid x=-2.75m så att den sedan hade följt just den bana som är given.
Skrev fel menade minus. Det var den lösningen som jag fick ut men råkade skriva fel på datorn
intealltidsåsmart skrev:Yngve skrev:Ja, du har gjort rätt på a-uppgiften.
På b-uppgiften gäller att symmetrilinjen ligger mitt emellan nollställena, dvs vid x = 13,75.
Bollen når alltså sin högsta höjd då = 13,75 meter.
Kommer du vidare då?
Vet inte. Om höjden är 13,75. Vad är då 30,2 för ngt? Är det det som är sträckan? Det är så jag tänker
Glöm detta om du läste det
naytte skrev:intealltidsåsmart skrev:Yngve skrev:Ja, du har gjort rätt på a-uppgiften.
På b-uppgiften gäller att symmetrilinjen ligger mitt emellan nollställena, dvs vid x = 13,75.
Bollen når alltså sin högsta höjd då = 13,75 meter.
Kommer du vidare då?
Vet inte. Om höjden är 13,75. Vad är då 30,2 för ngt? Är det det som är sträckan? Det är så jag tänker
Glöm detta om du läste det
???????
Verkar som att du blandat ihop vad x och h(x) står för. Från uppgiften:
x: bollens sträcka längst marken
h(x): höjd över marken
Du har med pq-formeln löst (h)x=0, dvs fått fram vilka x som ger höjden 0: x1=-2,73; x2=30,2
En andragradsfunktion har alltid sin max- (eller min-) punkt i symmetrilinjen, dvs för det x som ligger mitt emellan rötterna.
Mitt emellan ligger x=13,75.
Med detta x kan du beräkna h(x).
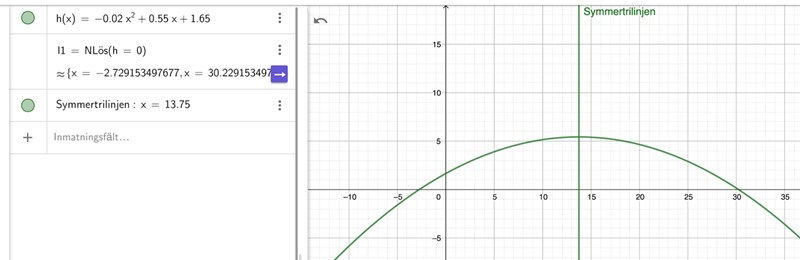
Notera att symmetrilinjen är samma sak som "halva koefficienten framför x med omvänt tecken" i pq-formeln vilket innebär att du inte ens behöver räkna ut x1 och x2 för att veta viket x som ligger mitt emellan.
(Edit: missade "med omvänt tecken" i meningen ovan.)
Programmeraren skrev:Verkar som att du blandat ihop vad x och h(x) står för. Från uppgiften:
x: bollens sträcka längst marken
h(x): höjd över markenDu har med pq-formeln löst (h)x=0, dvs fått fram vilka x som ger höjden 0: x1=-2,73; x2=30,2
En andragradsfunktion har alltid sin max- (eller min-) punkt i symmetrilinjen, dvs för det x som ligger mitt emellan rötterna.
Mitt emellan ligger x=13,75.
Med detta x kan du beräkna h(x).
Notera att symmetrilinjen är samma sak som "halva koefficienten framför x med omvänt tecken" i pq-formeln vilket innebär att du inte ens behöver räkna ut x1 och x2 för att veta viket x som ligger mitt emellan.
(Edit: missade "med omvänt tecken" i meningen ovan.)
Är A då alltså -2,73 och 30,2?
hänger inte riktigt med vad blir då det på fråga b? är det 13,75?
Funktionsvärdet h(x) är lika med bollens höjd ovan marken, då bollen har färdats x meter i horisobtell riktning.
Det betyder att
- h(1) är höjden ovan marken när bollen har färdats 1 meter i horisontell riktning
- h(2) är höjden ovan marken när bollen har färdats 2 meter i horisontell riktning
- och så vidare.
I a-uppgiften frågas det efter bollens höjd ovan marken när bollen har färdats 5 meter i horisontell riktning. Du ska alltså beräkna h(5).
I b-uppgiften frågas det efter vad bollens högsta höjd är och hur lång sträcka i horisontell riktning bollen har färdats då den når sin högsta höjd.
Vi har konstaterat att bollen når sin högsta höjd när den har färdats 13,75 meter i horisontell riktning. Bollens höjd är då h(13,75).
Blev det klarare då?
Yngve skrev:Funktionsvärdet h(x) är lika med bollens höjd ovan marken, då bollen har färdats x meter i horisobtell riktning.
Det betyder att
- h(1) är höjden ovan marken när bollen har färdats 1 meter i horisontell riktning
- h(2) är höjden ovan marken när bollen har färdats 2 meter i horisontell riktning
- och så vidare.
I a-uppgiften frågas det efter bollens höjd ovan marken när bollen har färdats 5 meter i horisontell riktning. Du ska alltså beräkna h(5).
I b-uppgiften frågas det efter vad bollens högsta höjd är och hur lång sträcka i horisontell riktning bollen har färdats då den når sin högsta höjd.
Vi har konstaterat att bollen når sin högsta höjd när den har färdats 13,75 meter i horisontell riktning. Bollens höjd är då h(13,75).
Blev det klarare då?
På ett sätt blev det mer klarare ja. Jag förstår uppgiften nu. Men om man ska räkna ut 5 meter som i a uppgiften så ska man inte sätta in 5 vid X. Hur gör man då, jag får fortfarande inte ihop det.
Jo, i a-uppgiften vet du värdet på x (x = 5). Då skall du bara sätta in 5 där det står x i formeln och räkna fram värdet h(5).
intealltidsåsmart skrev:
På ett sätt blev det mer klarare ja. Jag förstår uppgiften nu. Men om man ska räkna ut 5 meter som i a uppgiften så ska man inte sätta in 5 vid X. Hur gör man då, jag får fortfarande inte ihop det.
Visa hur du beräknar h(5) så hjälper vi dig att hitta eventuella fel.
Yngve skrev:intealltidsåsmart skrev:På ett sätt blev det mer klarare ja. Jag förstår uppgiften nu. Men om man ska räkna ut 5 meter som i a uppgiften så ska man inte sätta in 5 vid X. Hur gör man då, jag får fortfarande inte ihop det.
Visa hur du beräknar h(5) så hjälper vi dig att hitta eventuella fel.
Jag satte bara in 5 där det står X som jag skrev i inlägget. Om man inte ska göra på det sättet så är jag lost
Ja, det är så du ska göra.
Om du gör det och ändå får fel svar så kan vi hjälpa dig att hitta felet om du vill.
Men då måste du visa hur du räknar.
Yngve skrev:Ja, det är så du ska göra.
Om du gör det och ändå får fel svar så kan vi hjälpa dig att hitta felet om du vill.
Men då måste du visa hur du räknar.
Okej, varit många svar här som varit förvirrande. Jag har en inlämnings uppgift och därför finns det inget facit så jag kan inte veta om jag fått rätt svar eller inte. Men om det är 5 jag ska sätta in så har jag ju troligtvis gjort rätt på uträkningen.
h(5) = -0,020x^2 + 0,55x + 1,65 =
-0,020 * 5^2 + 0,55 * 5 + 1,65 =
-0,5 + 2,75 + 1,65 = 3,9
svaret är alltså 3,9 på fråga A. Det var det här jag gjorde från början men var inte säker på om jag tolkat uppgiften rätt, men det verkar ju som jag gjort det så jag tänker gå med det svaret om jag inte råkat räkna fel.
Fråga B å andra sidan är svårare, jag förstår inte vad det är jag har räknat ut? Och sedan blir det bara mer förvirrande.
Hur räknar man ut hur många meter bollen har åkt? jag fattar inte
Ska man bara sätta in 13,75 eller? Men isf om jag använde PQ formeln får jag ju också ut att x är -2,75 och 30,2. Vad är det för tal? ska man använda dem?
Ditt svar på a-uppgiften är rätt.
För b-uppgiften är det viktigt att du förstår hur en andragradsfunktion beter sig.
Läs igenom avsnittet som Smaragdalena länkade till i svar #4. Fråga sedan oss om allt du inte förstår där.
Yngve skrev:Ditt svar på a-uppgiften är rätt.
För b-uppgiften är det viktigt att du förstår hur en andragradsfunktion beter sig.
Läs igenom avsnittet som Smaragdalena länkade till i svar #4. Fråga sedan oss om allt du inte förstår där.
Jag kan inte koppla ihop siffrorna till sjävla frågan, att förstå en andragradsfuntion har jag koll på men får inte ihop det med själv frågan jag kan inte koppla ihop dem............ Jag fattar att X = -2,75 och 30,2 är där det skär i x axeln, men hur går man vidare därifrån och om man skulle förklara det med ord i förhållande till uppgiften. Asså det är att tolka själva frågan, framför allt som jag inte förstår.
Vad menar du med att tolka själva frågan? Vill du ha hjälp att förstå vad de frågar efter, dvs att förstå vad "bollens högsta höjd" och "hur lång sträcka längs med marken" egentligen betyder för en kastad boll?
Om det inte är det, utan att du istället behöver hjälp med hur du ska få fram svaret så vill jag att du svarar på följande frågor. Då blir det enklare för oss att hjälpa dig eftersom vi då ser vad det är du känner dig osäker på:
- Är du med på att grafen till funktionen h(x) är en parabel?
- Är du med på att en parabel alltid har en symmetrilinje?
- Vet du vad en symmetrilinje är?
- Är du med på att en parabels min- eller maxpunkt alltid ligger på symmetrilinjen?
- Är du med på att symmetrilinjen alltid ligger mitt emellan funktionens nollställen?
Jag vill veta hur man ska räkna ut och komma fram till svaren. Jag vet vad en symmetrilinje är, så ja jag är med på alla dem sakerna, men det hjälper inte till att förstå vad alla saker i frågan betyder, jag får inte ihop det till en bild. Jag förstår inte vad det är det frågar efter. Att dem vill veta bollens sträcka osv, det fattar jag såklart. Men vad är bollens höjd? och vad är bollens längd? Vad innebär dem sakerna i just denna fråga. Om man tar PQ formeln så vet jag ju att jag får ut punkter och kan rita upp dem, men jag fattar inte hur symmetrilinjen är relevant till en boll?
Efter mer än tjugo inlägg kan det vara lätt att glömma bort hur man började.
Pontus kastar iväg en boll så att dess höjd över marken, h(x), beror av bollens sträcka längs marken, x, enligt:
h(x) = -0,020x^2 + 0,55x + 1, 65. både bollens höjd och dess förflyttning, mäts i meter.
Hjälper det här dig?
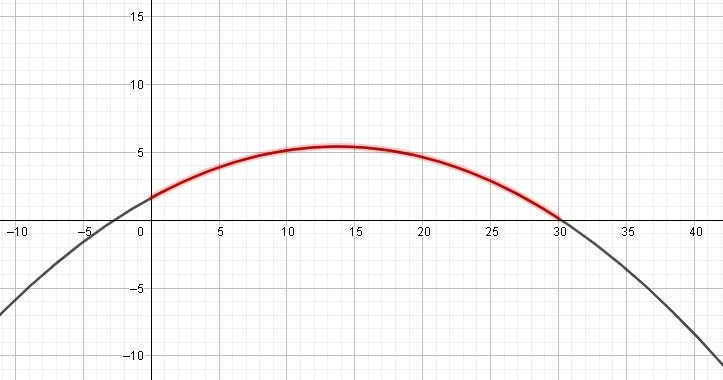
Jag har ritat upp funktionskurvan, precis som Programmeraren gjorde tidigare.
Där bollen börjar röra sig säger vi att x=0, och ju längre iväg den kommer desto högre flyger bollen - tills den når sin högsta punkt och rör sig neråt igen. Bollen kommer att röra sig på den rödmarkerade delen av funktionskurvan. Från x=0 tills bollen når marken igen efter ungefär 30 m.
Vi ser direkt att bollen är som högst upp lite innan den har åkt 15 meter bort.
Bubo skrev:Hjälper det här dig?
Jag har ritat upp funktionskurvan, precis som Programmeraren gjorde tidigare.
Där bollen börjar röra sig säger vi att x=0, och ju längre iväg den kommer desto högre flyger bollen - tills den når sin högsta punkt och rör sig neråt igen. Bollen kommer att röra sig på den rödmarkerade delen av funktionskurvan. Från x=0 tills bollen når marken igen efter ungefär 30 m.
Vi ser direkt att bollen är som högst upp lite innan den har åkt 15 meter bort.
Så som jag fattar det genom att kolla på detta diagram och av dem siffrorna jag fått ut, så skulle det betyda att bollen når sin högsta höjd vid 13,75 meter och att bollens sträcka då är mellan -2,73 - 30,3. allstå bollens sträcka blir då isf 32,76 meter? Men det kan ju inte stämma..............
Annars så tänker jag att 0,020x^2 + 0,55x + 1, 65 = 13,75?
Men det kan ju heller inte stämma och om det gör det hur får man ut x isf, det går inte ihop. Sätter man in 13,75 blir det ju 0. Så att säga att h(13,75) blir inte logiskt i min hjärna. Eftersom i den första ekvationen så betyder h(5) meter och att man ska sätta in 5. Man eftersom att man inte ska sätta in 13,75 i ekvationen så kan man väll inte säga att h(13,75)?
h(x) betyder Bollens höjd på avståndet x från kastaren.
h(5) = 3.9. Fem meter bort från kastaren är bollen 3.9 meter över marken.
h(0) = 1.65 Precis vid kastaren är bollen 1.65 meter över marken. (Han håller ju bollen i handen).
h(13.75) talar om hur högt bollen är 13.75 meter från kastaren.
h(-2.73) talar om hur högt bollen skulle ha varit 2.73 meter bakom kastaren, men där är den ju aldrig. Bollen rör sig längs röd kurva, och vi struntar i rörelsen efter att den har landat.
Bubo skrev:h(x) betyder Bollens höjd på avståndet x från kastaren.
h(5) = 3.9. Fem meter bort från kastaren är bollen 3.9 meter över marken.
h(0) = 1.65 Precis vid kastaren är bollen 1.65 meter över marken. (Han håller ju bollen i handen).
h(13.75) talar om hur högt bollen är 13.75 meter från kastaren.
h(-2.73) talar om hur högt bollen skulle ha varit 2.73 meter bakom kastaren, men där är den ju aldrig. Bollen rör sig längs röd kurva, och vi struntar i rörelsen efter att den har landat.
Hur får man ut x då isf?
Edit: Men vänta. Om 13,75 är hur högt bollen är från kastaren, så blir inte 13,75 högsta höjden? Eller är det samma sak? Hur får man ut hur långt bollen har åkt?
Edit 2: Okej jag skrev fel i inlägget åvan och slog helt fel på miniräknaren. Om man sätter in 13,75 blir det naturligvis inte 0. Räknade in 30,2 och kollade fel på mina anteckningar. Om man sätter in 13,75, blir det ungefär 9,7. Är det det som blir meter? Ska man sätta in 13,75 för att få fram meter?
Isf blir högsta höjden = 13,75 och att den då har åkt 9,7 meter efter marken. Och som programeraren skrev så är 30,2 och -2,73 helt orelevant till att räkna ut hur många meter efter marken som den har åkt.
Alltså blir svaret till frågan att högsta höjden då är 13,75 och att den då har åkt 9,7 meter efter marken? Är det dn uträkningen som är korrekt isf?
Edit 3: Räknade fel igen.................. Om man sätter in 13,75 får man ut ca 5,4. Måste slagit fel på miniräknaren.
I vilket fall ska man bara sätta in 13,75 i ekvationen eller inte? Svaret jag får ut verkar inte logiskt vilket får mig att tänka att det inte är så man ska göra
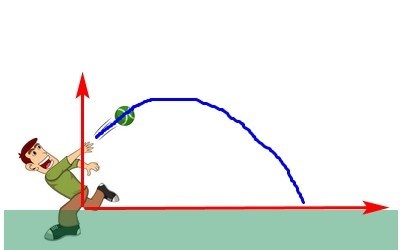
Vi backar lite. Vad är den här funktionen egentligen?
Vad är x och vad är h(x)? Läs inte för mycket i tidigare inlägg nu, utan svara med egna ord.
Här är en bild:
Bubo skrev:Vi backar lite. Vad är den här funktionen egentligen?
Vad är x och vad är h(x)? Läs inte för mycket i tidigare inlägg nu, utan svara med egna ord.
Här är en bild:
h(x) = Hur många meter bort från kastaren som bollen är och x är höjden.
Därav så blir 13,75 meter och höjden är fortfarande okänd
Vilket också då gör det logiskt att man ska sätta in 13,75 i ekvationen för att få ut höjden. Är det rätt eller fel?
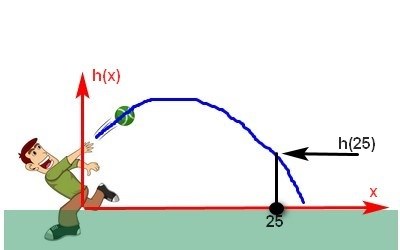
Aha. Du har missuppfattat. Det är tvärtom:
x är sträckan längs marken, och h(x) är höjden.
3 meter från kastaren säger vi att x är 3, och att bollen flyger h(3) meter över marken.
Bubo skrev:Aha. Du har missuppfattat. Det är tvärtom:
x är sträckan längs marken, och h(x) är höjden.
3 meter från kastaren säger vi att x är 3, och att bollen flyger h(3) meter över marken.
okej så då är 13,75 alltså höjden? Hur får man ut meter? eller va? nu blev jag bara mer förvirrad är 13,75 höjden eller sträckan?
Jag tror att det är bäst att du börjar om, så att du inte använder det du fick fram när du missuppfattade.
Visa spoiler
Vi har fått fram att h(x) har ett maximum för x=13.75. Vad betyder det?
Bubo skrev:Jag tror att det är bäst att du börjar om, så att du inte använder det du fick fram när du missuppfattade.
Visa spoiler
Vi har fått fram att h(x) har ett maximum för x=13.75. Vad betyder det?
Det spelar ingen roll om jag börjar om eller inte kommer ju fortfarande få fram 13,75 om jag använder PQ formeln, svaret kommer ju bli samma. Ska jag sätta in 13,75 i ekvationen eller inte för ut den andra delen av svaret, eftersom att h(13,75) är avståndet från kastaren så är det ju höjden jag ska räkna ut.
Jag ska ju räkna ut vad x:et är i ekvationen. Jag har gjort det och kommit fram till ett svar som jag skrivit tidigare och undrar om jag har gjort rätt eller om det är något som jag råkat missat.
Jag har alltid antagit att 13,75 är meter, men denna tråd gjorde mig jätte förvirrad. Så nu tänker jag skriva att 13,75 är avståndet i meter eftersom det är det som alla här håller med om.
Mitt svar till denna uppgift lyder:
Bollens högsta höljd är 5,4 när den har åkt 13,75 m längst marken.
Det jag vill veta är, ska man sätta in 13,75 i ekvationen, ja eller nej? Och är mitt svar korrekt?
Edit: Har inget facit så svaret kan jag inte kontrollera, men undrar om jag gjort uträkningen korrekt
intealltidsåsmart skrev:Bubo skrev:Jag tror att det är bäst att du börjar om, så att du inte använder det du fick fram när du missuppfattade.
Visa spoiler
Vi har fått fram att h(x) har ett maximum för x=13.75. Vad betyder det?
Det ser ut som om du tänker rätt, men du skriver lite motsägelsefullt. Svaret Bollens högsta höljd är 5,4 när den har åkt 13,75 m längst marken. är rätt,
Ja, alla sträckor räknas i meter. Om beskrivningen verkar lite krånglig så beror det på att vi vill räkna på x och h(x) utan att behöva skriva "meter" på så många ställen.
Jag har använt "avstånd" när jag menar "vågrätt avstånd", alltså mätt längs marken.
Det spelar ingen roll om jag börjar om eller inte kommer ju fortfarande få fram 13,75 om jag använder PQ formeln, svaret kommer ju bli samma. Ska jag sätta in 13,75 i ekvationen eller inte för ut den andra delen av svaret, eftersom att h(13,75) är avståndet från kastaren så är det ju höjden jag ska räkna ut.
Jag är inte riktigt med på vad du menar med "eftersom att h(13,75) är avståndet från kastaren så är det ju höjden jag ska räkna ut. "
Jag ska ju räkna ut vad x:et är i ekvationen. Jag har gjort det och kommit fram till ett svar som jag skrivit tidigare och undrar om jag har gjort rätt eller om det är något som jag råkat missat.
Jag har alltid antagit att 13,75 är meter, men denna tråd gjorde mig jätte förvirrad. Så nu tänker jag skriva att 13,75 är avståndet i meter eftersom det är det som alla här håller med om.
Mitt svar till denna uppgift lyder:
Bollens högsta höljd är 5,4 när den har åkt 13,75 m längst marken.
Ja, bollens högsta höljd är 5,4 m när den har åkt 13,75 m längst marken.
Det jag vill veta är, ska man sätta in 13,75 i ekvationen, ja eller nej?
Ja.
Och är mitt svar korrekt?
Edit: Har inget facit så svaret kan jag inte kontrollera, men undrar om jag gjort uträkningen korrekt
Svaret är korrekt. Det vore snyggt med en fullständig lösning. Vi har alla pusselbitar till lösningen nu.
Bubo skrev:intealltidsåsmart skrev:Bubo skrev:Jag tror att det är bäst att du börjar om, så att du inte använder det du fick fram när du missuppfattade.
Visa spoiler
Vi har fått fram att h(x) har ett maximum för x=13.75. Vad betyder det?
Det ser ut som om du tänker rätt, men du skriver lite motsägelsefullt. Svaret Bollens högsta höljd är 5,4 när den har åkt 13,75 m längst marken. är rätt,
Ja, alla sträckor räknas i meter. Om beskrivningen verkar lite krånglig så beror det på att vi vill räkna på x och h(x) utan att behöva skriva "meter" på så många ställen.
Jag har använt "avstånd" när jag menar "vågrätt avstånd", alltså mätt längs marken.
Det spelar ingen roll om jag börjar om eller inte kommer ju fortfarande få fram 13,75 om jag använder PQ formeln, svaret kommer ju bli samma. Ska jag sätta in 13,75 i ekvationen eller inte för ut den andra delen av svaret, eftersom att h(13,75) är avståndet från kastaren så är det ju höjden jag ska räkna ut.
Jag är inte riktigt med på vad du menar med "eftersom att h(13,75) är avståndet från kastaren så är det ju höjden jag ska räkna ut. "
Jag ska ju räkna ut vad x:et är i ekvationen. Jag har gjort det och kommit fram till ett svar som jag skrivit tidigare och undrar om jag har gjort rätt eller om det är något som jag råkat missat.
Jag har alltid antagit att 13,75 är meter, men denna tråd gjorde mig jätte förvirrad. Så nu tänker jag skriva att 13,75 är avståndet i meter eftersom det är det som alla här håller med om.
Mitt svar till denna uppgift lyder:
Bollens högsta höljd är 5,4 när den har åkt 13,75 m längst marken.
Ja, bollens högsta höljd är 5,4 m när den har åkt 13,75 m längst marken.
Det jag vill veta är, ska man sätta in 13,75 i ekvationen, ja eller nej?
Ja.
Och är mitt svar korrekt?
Edit: Har inget facit så svaret kan jag inte kontrollera, men undrar om jag gjort uträkningen korrekt
Svaret är korrekt. Det vore snyggt med en fullständig lösning. Vi har alla pusselbitar till lösningen nu.
Ursäkta att jag skriver lite motsägelsefullt, jag kan se nu att det har blivit fel när jag har skrivit. "Höjden" blir x, och avståndet blir h(x), det är det bästa sättet jag kan förklara det på. Blir kanske enklare att säga att man ska lösa X. Jag vet inte
Men okej då var denna uppgift löst iaf. Det blev en del förvirring med jag fattar nu, så tack för hjälpen!
Nej, nu blev det tvärtom igen.
Höjden är inte x. Avståndet längs marken är inte h(x).
Höjden är h(x). Avståndet längs marken är x.
intealltidsåsmart skrev:Men okej då var denna uppgift löst iaf. Det blev en del förvirring med jag fattar nu, så tack för hjälpen!
Jag tror att det viktigt att du verkligen förstår kopplingen mellan den fysikaliska verkligheten (hur bollen rör sig i luften) och den matematiska modellen av denna verklighet (vad x och h(x) står för) innan du släpper den här uppgiften och går vidare.
Yngve skrev:intealltidsåsmart skrev:Men okej då var denna uppgift löst iaf. Det blev en del förvirring med jag fattar nu, så tack för hjälpen!
Jag tror att det viktigt att du verkligen förstår kopplingen mellan den fysikaliska verkligheten (hur bollen rör sig i luften) och den matematiska modellen av denna verklighet (vad x och h(x) står för) innan du släpper den här uppgiften och går vidare.
Ja men nu fattar jag ju vad det står för när jag räknat ut den
b-uppgiften)
Lös rötterna till ekvationen och räkna ut x-värdet vid symmetrilinjen:
intealltidsåsmart skrev:
Ja men nu fattar jag ju vad det står för när jag räknat ut den
Bra, då tar vi ett par kontrollfrågor:
- Hur högt ovanför marken var bollen då Pontus kastade den?
- Hur långt kastade Pontus bollen?





