En cirkelsektor har omkretsen 10 cm. Beräkna den största arean

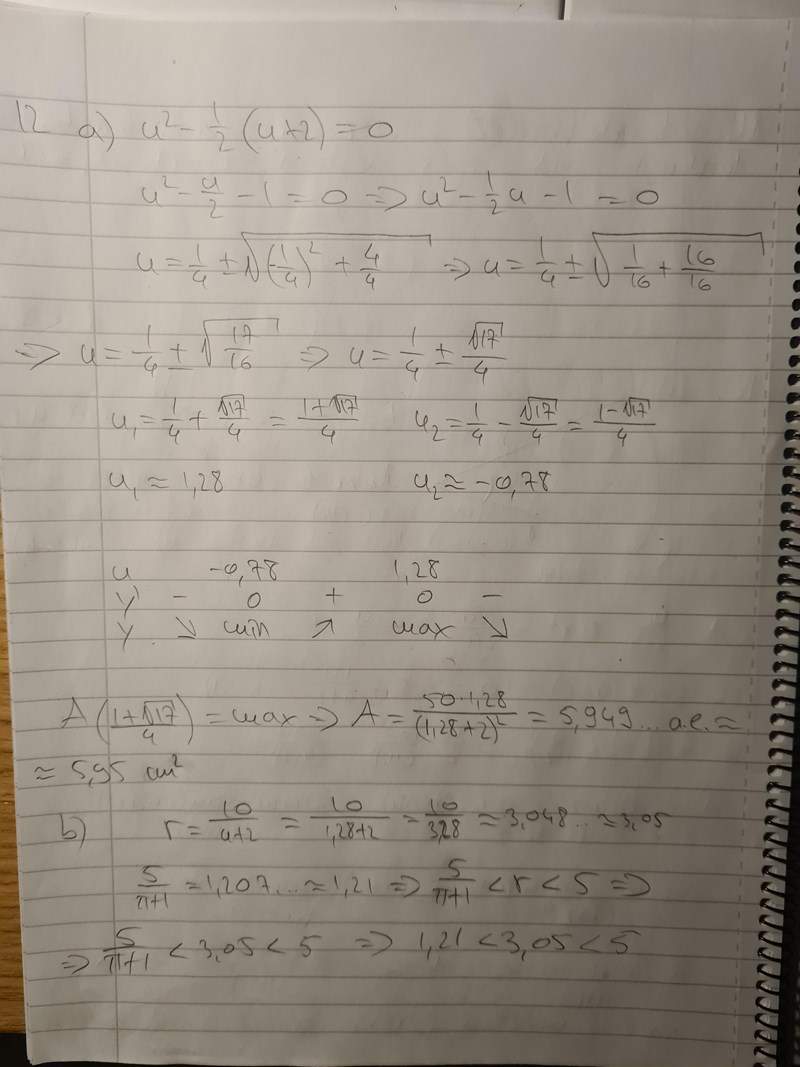
Du kan kolla svaret genom att räkna ut arean för ett något mindre och ett något större värde än det r du har kommit fram till.

A' ser inte helt rätt ut. Du har fått med ett u för mycket när du deriverar (u+2)².

Ett sätt att göra det enklare för sig är att införa en ny variabel t = u+2.

Hej och tack för svaret! 

Jag har nu åtgärdat misstaget. Ser lösningen bra ut? 

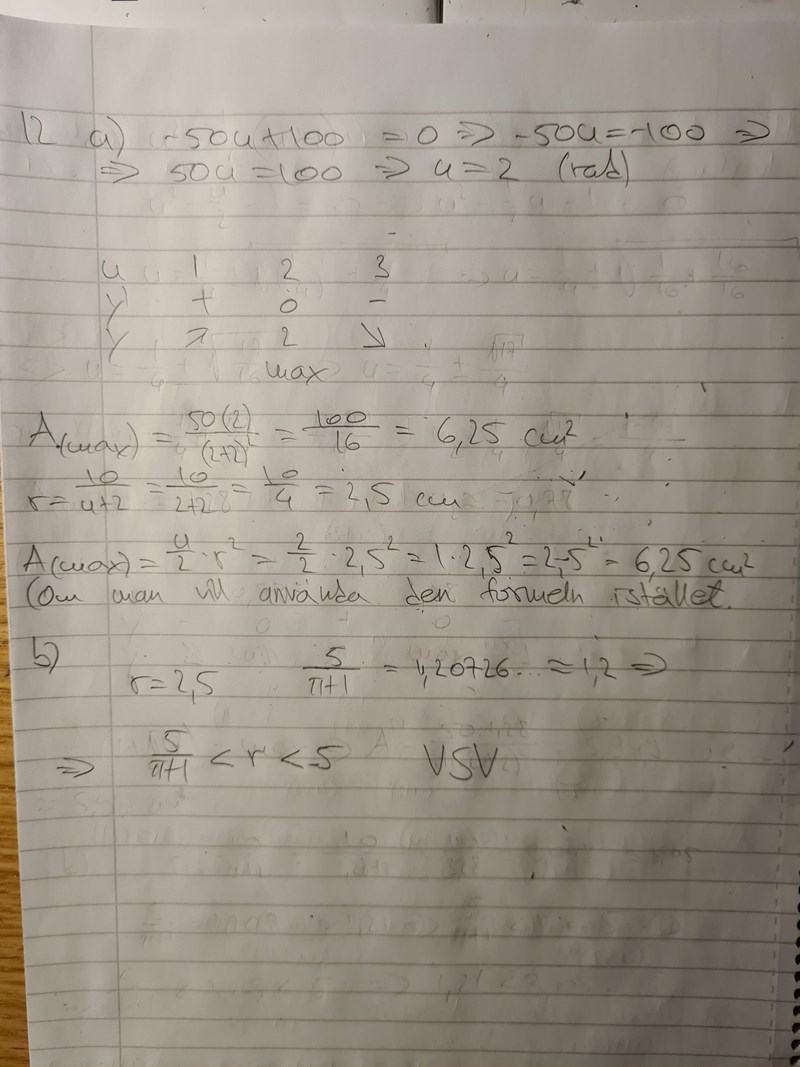
a) ser rätt ut.

Ett tips inför framtida uppgifter är att när du kan välja att bryta ut två variabler kan det vara värt att testa båda innan man börjar derivera. Du bröt ut r och skrev arean som en funktion av u. Men du hade fått en mycket lättare derivering om du i stället brutit ut u och skrivit arean som en funktion av r. Båda funkar och du har gjort rätt, men gör man på det senare sättet får man $A\left(r\right)=-r^2+5r$, som är lättare att derivera.

På b tror jag att du har missuppfattat frågan. Du ska inte bevisa att påståendet gäller för sektorn med den största arean, utan för alla cirkelsektorer med omkretsen 10 cm. Du kan resonera så här:

1. Kan radien vara hur stor som helst? Nej, för om den är tex 10 cm kan man aldrig göra en cirkelsektor med omkretsen 10 cm. Vad är det största den kan vara?

2. Kan radien vara hur liten som helst? Nej, för om den är tex 0,1 cm kan man aldrig göra en cirkelsektor med omkretsen 10 cm. Vad är det minsta den kan vara?

Tack för svaret. Ska man derivera funktionen för r för att få fram största och minsta värde för r där omkretsen är 10 cm eller hur ska man göra i så fall?

Ja, det låter som en bra plan.

Jag började såhär, men kommer inte längre än så.

Nja, jag skulle nog hellre föreslå att du använder den metod jag var inne på i mitt förra inlägg. Läs det igen!

Förstår du att radien inte kan vara hur stor som helst? Omkretsen är ju $2r+vr$ (om vinkeln mäts i radianer). Om r > 5 blir 2r > 10 och då blir 2r+vr större än 10 för v och r är ju positiva tal! Om r = 5 måste vr = 0 om omkretsen ska bli 10 och då måste v = 0, och då har man ju ingen cirkelsektor alls. Alltså måste r < 5, och då är ena delen av olikheten du ska bevisa klar.

Kan du använda ett liknande resonemang för att bevisa $\frac{5}{\mathrm{\pi }+1}<r$?

Hej! 

Jag förstår att radien inte kan vara hur stor och inte hur liten som helst. Tack för hjälpen. Jag har påbörjat lösningen med din metod, men jag har fastnat lite i slutet. Jag har använt mig av motsägelsebevis, precis som du. 

Du tänker rätt men du gör ett vanligt fel, nämligen att du börjar med det du ska bevisa, och jobbar mot det du vet. Så kan man göra när man tänker ut beviset, men när man presenterar det måste man börja med det man vet, och härleda det man ska bevisa från det.

Då kan man till exempel börja med att $u<2\mathrm{\pi }$. Sedan kan man göra på två sätt. Det ena är att man bara skriver formler. Att omkretsen är 10 ger:

$$\begin{gathered} 2r+ur=10 \\ ur=10-2r \\ u=\frac{10-2r}{r} \end{gathered}$$

$u<2\mathrm{\pi }\Rightarrow \frac{10-2\mathrm{r}}{\mathrm{r}}<2\mathrm{\pi }$

$$\begin{gathered} \frac{10-2r}{r}<2\mathrm{\pi } \\ 10-2\mathrm{r}<2\mathrm{\pi r} \\ 5-\mathrm{r}<\mathrm{\pi r} \\ 5<\mathrm{\pi r}+\mathrm{r} \\ 5<\mathrm{r}\left(\mathrm{\pi }+1\right) \\ \frac{5}{\mathrm{\pi }+1}<\mathrm{r} \end{gathered}$$

Det andra är att man resonerar sig fram ungefär så här:

Om vinkeln vore exakt $2\mathrm{\pi }$ skulle radien behöva vara = $\frac{10}{2+u}=\frac{10}{2+2\mathrm{\pi }}=\frac{5}{\mathrm{\pi }+1}$

Men vinkeln måste vara mindre än $2\mathrm{\pi }$ så då måste raden vara större, och då får man olikheten $r>\frac{5}{\mathrm{\pi }+1}$

Bägge sätten funkar men det andra är kanske lite lättare att följa.

Tack för hjälpen! 

SvanteR skrev:

a) ser rätt ut.

Ett tips inför framtida uppgifter är att när du kan välja att bryta ut två variabler kan det vara värt att testa båda innan man börjar derivera. Du bröt ut r och skrev arean som en funktion av u. Men du hade fått en mycket lättare derivering om du i stället brutit ut u och skrivit arean som en funktion av r. Båda funkar och du har gjort rätt, men gör man på det senare sättet får man $A\left(r\right)=-r^2+5r$, som är lättare att derivera.

 

Ber om ursäkt om det inte är tillåtet att skriva i gamla trådar, men gör ett försök ändå. 

Skulle någon vilja förklara hur jag bör göra efter att jag brutit ut u istället för r? 

Såhär har jag gjort: 
u = (10/r)-2

Sätter in u i areaformel för cirkelsektor: 

((10/r)-2)/(2pi) = ((5/r)-1)/(pi)

((5/r)-1)/(pi) * pi*r^2 = r^2((5/r)-1)

Här kör jag fast. 

Det är tillåtet att skriva i gamla trådar men eftersom trådstartaren markerat att denne är klar med tråden, så är risken att ingen går in och tittar på tråden. Du har nog störst chans att få hjälp om du skapar en egen tråd, Gozpena. Lycka till! /Jonto, moderator