endimensionell analys, gränsvärde - Kluring (Matematik/Universitet)

OK, om det inte är en kluring är den enkel nog. Så det är en hund begraven, men jag ser inte var.

Den kanske är lika enkel som du tror. Det beror lite på hur man angriper gränsvärdet. :)

Bryt ut x i täljaren och nämnaren. => $\frac{1}{1 + \frac{\sin x}{x}} - > 1 e f t e r s o m \frac{\sin x}{x} = 0 d å x - > \infty$

Stämmer. Att visa att sinx/x går mot 0 följer väldigt snabbt efter man stänger in sinx. :)

Det intressanta är om man istället tänker sig att man vill använda L'Hôpitals regel och inte är försiktig. :)

Dracaena skrev:
Stämmer. Att visa att sinx/x går mot 0 följer väldigt snabbt efter man stänger in sinx. :)

Det intressanta är om man istället tänker sig att man vill använda L'Hôpitals regel och inte är försiktig. :)

Med l'Hopital ser jag inte hur den kan konvergera. Du kanske har ett trick?

Nej, du har helt rätt. Om vi applicerar L'Hôpitals regel så får vi en funktion vars gränsvärde inte existerar.

Många elever överanvänder L'Hôpitals regel utan att egentligen veta vad som krävs.

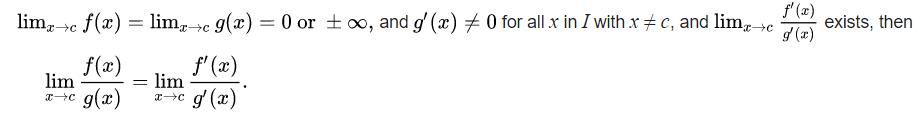
Man vet eller glömmer nästan alltid bort det andra villkoret. I detta fallet om man inte är försiktig så konkluderar man att gränsvärdet inte existerar.

Med andra ord, du föll inte för fällan! :)

Hade väl tur, jag. Reflekterade aldrig över l’Hôpital.

Det är väl kanske mer naturlig för någon som är lite rutinerad med gränsvärden att börja fundera på Instängningssatsen när man har en trigonometrisk funktion.

Jag tror jag hade en bra lärare. Han höll L’Hôpital hemlig tills det var några dagar kvar till tentan.

Som vår gymnasielärare som i det längsta smusslade med andraderivatatestet. Vi skulle lära oss att göra teckenscheman.

Vi fick använda den omm vi nämnde alla villkoren och bevisade satsen. Utöver det så gick vi aldrig igenom den.

Vi fick istället kämpa med grisiga standardgränsvärden. Livet kunde inte bli bättre när man lärde sig om maclaurinutveckling.

Dracaena skrev:
Vi fick använda den omm vi nämnde alla villkoren och bevisade satsen. Utöver det så gick vi aldrig igenom den.

Vi fick istället kämpa med grisiga standardgränsvärden. Livet kunde inte bli bättre när man lärde sig om maclaurinutveckling.

Maclaurinutvecklingar är guds gåva tills uppgifter kräver ett fullständigt bevis. Då önskar man att man hade spenderat mer tid på standardgränsvärden.

(btw: kan man inte bara stänga in funktionen och utnyttja att sinus är begränsad)

Jo, det är väl det enklaste sättet att bevisa att sinx/x går mot 0 som rapidos använder ovan.

$-1 \leq \sin x \leq 1$

$\dfrac{-1}{x} \leq \dfrac{\sin x}{x} \leq \dfrac{1}{x}$

$0 \leq \dfrac{\sin x}{x} \leq 0$

Vilket Konkluderar att det går mot $0$ .

Tack för den tråden Dracaena!

Den kom ganska lämpligt för mig nu. Visserligen ligger l'Hopitals regel en bit bort än så länge, men det närmar sig.

En bieffekt blev att regeln $\lim_{x \to 0} = \frac{\sin (x)}{x} = 1$ blev tydligare då man tänker på

$\lim_{x \to \infty} \frac{\sin (x)}{x} = 0$ eftersom att sin(x) varierar mellan -1 och +1 och nämnaren blir större och större så blir resultatet noll.

Det inspirerade mig också att undersöka $\frac{1 - \cos (x)}{x} och \frac{\cos (x) - 1}{x}$ vilket också är intressant.

Då kom en fundering som jag haft länge, varför har vi inte matematiska laborationer? Det borde väl vara utvecklande?

Jag hade laborationer i alla mina kurser. Men du kanske tänker på någon annan sorts laboration?

Prova till exempel att stänga in $\dfrac{\cos x -1}{x}$ som en övning. :)

The Squeeze Theorem är väldigt användbar att lära sig när man börjar pilla med gränsvärden som inte bara är rena polynom. :)

Wow det där med Squeeze Theorem får jag studera lite djupare. Det ingick lite ytligt i Adams Calculus, men bara som appendix i Simons Calculus. Känns som ytterligare ett exempel på något man ska känna till redan innan kursen?

Har du exempel på mattelaborationer? Eller menar du bara undersökningar du gjort på eget bevåg?

Nej, jag menar riktiga laborationer! :)

I endimensionell analys exemeplvis så använde vi Mathematica för att skapa ett larmsystem. Det byggde för det mesta på differentialekvationer. Så man kan väl se det som en labb inom ellära. Det var dock i princip bara matematik eftersom det handlade för det mesta att hitta eller teckna rätt diffar och lösa det analytiskt.

Vi har gjort liknande i många av mina kurser. Sedan så kan man ofta få bonuspoäng på tentor genom att lösa extra uppgifter (seminarium) och redovisa dessa på ett givet tillfälle.

Känns som ytterligare ett exempel på något man ska känna till redan innan kursen?

Inte ett måste. Man lär sig detta i endimen. Det klassas väl som ett basic verktyg för att lösa gränsvärden på den nivån. Lite som att bryta ut dominerande faktorer är ganska basic för matte 4 gränsvärden.

Om du hellre vill läsa envarren på svenska förresten så rekommenderar jag starkt endim av Jonas Månsson. Han har också en massa videos på youtube som är fantastiska.

Dracaena skrev:

Känns som ytterligare ett exempel på något man ska känna till redan innan kursen?

Inte ett måste. Man lär sig detta i endimen. Det klassas väl som ett basic verktyg för att lösa gränsvärden på den nivån. Lite som att bryta ut dominerande faktorer är ganska basic för matte 4 gränsvärden.

Om du hellre vill läsa envarren på svenska förresten så rekommenderar jag starkt endim av Jonas Månsson. Han har också en massa videos på youtube som är fantastiska.

Jag var lite för snabb där. I Adams Calculus så förklarar man att Squeez-metoden kommer att användas mer i kommande kapitel.
Jonas Månsson är ett mycket bra förslag ser jag. Han förklarade instängningssatsen bra för sin(x)/x så där kan jag nog hämta en hel del. Tack för den!

Om jag skulle ge mig på $\lim_{x \to 0} \frac{1 - \cos (x)}{x}$ som övning efter Jonas Månssons genomgång, så blir min början så här:

$(1 - \cos (x)) < x < \tan (x)$ dividerar med cos(x) och får $\frac{1}{\cos (x)} - \frac{\cos (x)}{\cos (x)} < \frac{x}{\cos (x)} < \frac{\tan (x)}{\cos (x)}$

Vilket blir 1-1<x<sin(x)/cos²(x) och slutligen 0<x<0 när x går mot noll.

Kan det vara en lämplig början?

Tillägg: 25 nov 2022 07:20

Jag ser ett problem med min lösning. Den fungerar endast om vi låter $\lim_{x \to 0^{+}}$

Gör det att det inte är någon riktig lösning?

Tillägg: 25 nov 2022 07:30

Eller jo det går från $\lim_{x \to 0^{-}}$ också, men ja det ser inte riktigt rätt ut?

Tillägg: 25 nov 2022 07:38

Tillägg: 25 nov 2022 11:22

Om vi lägger till att när vi låter $\lim_{x \to 0^{-}}$

så gäller att $\tan (x) < x < (1 - \cos (x))$

blir det giltigt då?

Jag börjar att bli tveksam till mitt försök. Det verkar inte att hålla vid närmare granskning.
Jag har försökt förstå länken du hänvisade till "Squeeze theorem", men förstår inte
"for x close enough to 0. This can be derived by replacing sin(x) in the earlier fact by $\sqrt{1 - \cos^{2} (x)}$ and squaring the resulting inequality."

Edit: OK jag tror jag förstår. De syftar på den vanliga härledningen, där vi först multiplicerar täljaren och nämnaren med täljarens konjugat och sedan använder resultatet av instängningsmetoden vid härledningen av $\lim_{x \to 0} \frac{\sin (x)}{x}$ som Jonas Månsson så fint beskrev. Så egentligen använder man inte instängningsmetoden i detta fall utan endast indirekt.

Om du kikar på det geometriska beviset till höger så ser du en rad olikheter man kan ta fram.

Vi kan helt enkelt använd att vi vet vad sinx/x går mot.

En annan lösning är att använda standardgränsvärden:

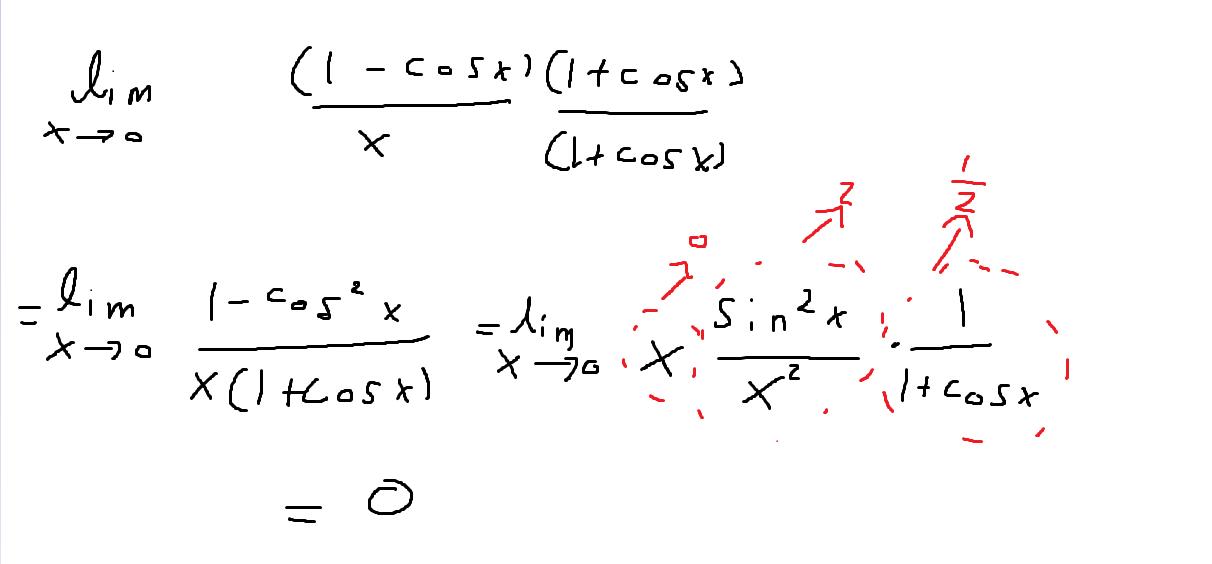
Jag har egentligen slarvat ser jag nu, sin^2(x)/x^2 går mot 1 och inte 2, men i just detta fallet så spelar det ingen roll eftersom x går mot 0.

Om vi utgår från figuren nedan så gör jag ett nytt försök.

Vi ser att (1-cos(x)) < (1-cos(x))/x < tan(x)

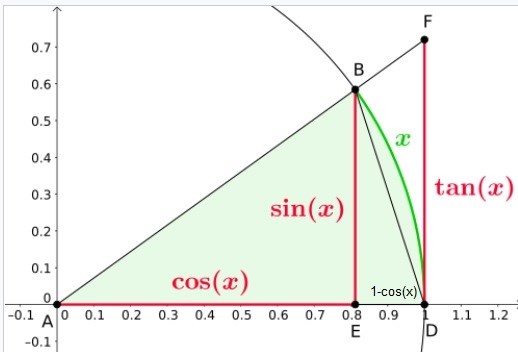
Detta gäller när vi låter $x \to 0^{+}$ och x < 1
När x går mot 0 går (1-cos(x)) mot noll och tan(x) går mot noll.
Då har vi klämt in (1-cos(x))/x mellan 0 och 0 och har det geometriska beviset för det klart.
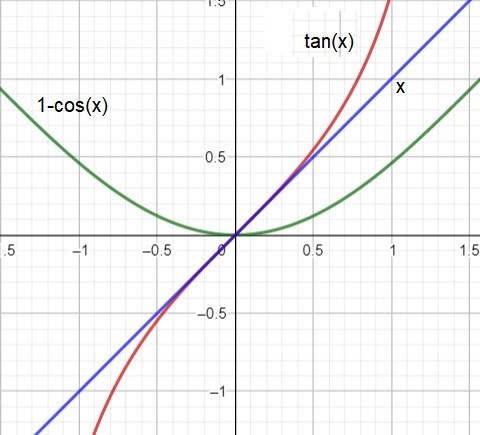
Vi ser att det stämmer med denna figur där f(x) = (1-cos(x)), g(x) = (1-cos(x))/x
och h(x) = tan(x)

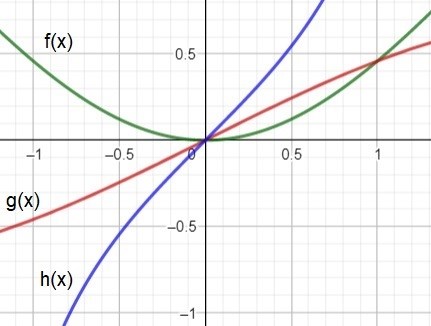
Om vi låter $x \to 0^{-}$ så ser vi att tan(x) < (1-cos(x))/x < (1-cos(x)) och även där ser vi att det stämmer.

Jag tror att jag har fått lite bättre kläm på detta nu.
Kommentera gärna.

Idag blir det inte så mycket mer matematik då jag idag fyller 70 år vilket känns lite extra högtidligt.

Det ser Rimlgit ut!

Grattis på sjuttio-års-dagen Conny! :)