Enhetscirkeln
Hej :)
Jag har ritat upp enhetscirkeln för sinx = -0.5, och ville bara dubbelkolla så jag gjort rätt, ska ha den för att bevisa att det finns två lösningar bara :)
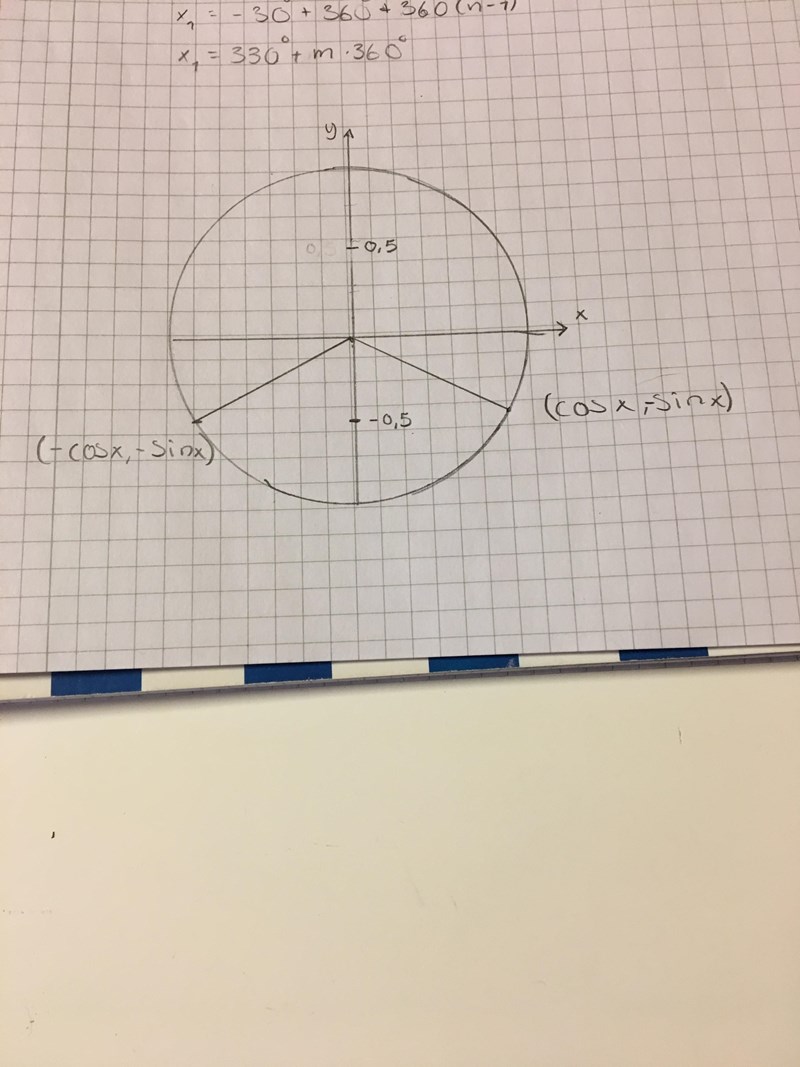
Det finns oändligt många lösningar till ekvationen eftersom man kan lägga till ett godtyckligt antal hela varv också.
Smaragdalena skrev:Det finns oändligt många lösningar till ekvationen eftersom man kan lägga till ett godtyckligt antal hela varv också.
Så egentligen behöver jag inte enhetscirkeln? jag har löst uppgiften redan där jag fick till två svar, tänke man behövde bevisa med enhetscirkeln varför jag får två svar :)
Slarva inte när du ritar figuren.
Vad är x? Har du några teckenfel?
Corokia cotoneaster skrev:Hej :)
Jag har ritat upp enhetscirkeln för sinx = -0.5, och ville bara dubbelkolla så jag gjort rätt, ska ha den för att bevisa att det finns två lösningar bara :)
Du har ritat enhetscirkeln rätt och visat att ekvationen har två lösningar i intervallet , vilket är rätt. Se dock nedan invändning kring vinkel och x.
Det går inte riktigt att se vad du har skrivit där uppe, men det ser ut som att du helt korrekt har lagt till en periodicitet (dvs att du lagt till n*360° till båda lösningarna). Däremot har du kallat båda lösningsmängderna för , vilket är förvirrande och på den översta raden ser det ut som om du skrivit .
Varför det extra 360° och varför (n-1)?
En annan stor invändning är att du inte ska benämna koordinataxlarna x och y i detta fallet eftersom ekvationen du arbetar med är sin(x) = -0,5 dvs x betecknar en vinkel.
Det är då alldeles för stor risk att du blandar ihop koordinaten x med vinkeln x.
Sedan har du angivit koordinaterna fel för de två punkterna där strålarna skär enhetscirkeln. För att de ska bli tolkningsbara måste du ange i figuren vad du anser att (vinkeln) x är.
Corokia cotoneaster skrev:Smaragdalena skrev:Det finns oändligt många lösningar till ekvationen eftersom man kan lägga till ett godtyckligt antal hela varv också.
Så egentligen behöver jag inte enhetscirkeln? jag har löst uppgiften redan där jag fick till två svar, tänke man behövde bevisa med enhetscirkeln varför jag får två svar :)
Det är bra att visa hur lösningarna ligger med hjälp av enhetscirkeln. Men det är då viktigt att inte skriva fel, se tidigare svar.
Yngve skrev:Corokia cotoneaster skrev:Hej :)
Jag har ritat upp enhetscirkeln för sinx = -0.5, och ville bara dubbelkolla så jag gjort rätt, ska ha den för att bevisa att det finns två lösningar bara :)
Du har ritat enhetscirkeln rätt och visat att ekvationen har två lösningar i intervallet , vilket är rätt. Se dock nedan invändning kring vinkel och x.
Det går inte riktigt att se vad du har skrivit där uppe, men det ser ut som att du sedan helt korrekt har lagt till en periodicitet (dvs att du lagt till n*360° till båda lösningarna). Däremot har du kallat båda lösningsmängderna för , vilket är förvirrande och på den översta raden ser det ut som om du skrivit .
Varför det extra 360° och varför (n-1)?
En annan stor invändning är att du inte ska benämna koordinataxlarna x och y i detta fallet eftersom ekvationen du arbetar med är sin(x) = -0,5 dvs x betecknar en vinkel.
Det är då alldeles för stor risk att du blandar ihop koordinaten x med vinkeln x, vilket du verkar ha gjort när du anger koordinater för de två punkterna där strålarna skär enhetscirkeln.
Nu blev jag lite osäker har letat rätt på hur jag skulle göra med perioderna i boken fram å tillbaka. lägger in uppgiften och vad jag gjort:
Lös ekvationen (sin x)2 1 = 1,5 sin x
Det jag gjort:
.jpg?width=800&upscale=false)
.jpg?width=800&upscale=false) Blev osäker angående över hur jag lagt till perioden. Kan ha blandat ihop massa saker som stod i boken.
Blev osäker angående över hur jag lagt till perioden. Kan ha blandat ihop massa saker som stod i boken.
Corokia cotoneaster skrev:
Nu blev jag lite osäker har letat rätt på hur jag skulle göra med perioderna i boken fram å tillbaka. lägger in uppgiften och vad jag gjort:
Lös ekvationen (sin x)2 1 = 1,5 sin x
Det jag gjort:
Blev osäker angående över hur jag lagt till perioden. Kan ha blandat ihop massa saker som stod i boken.
Du har gjort rätt, men jag skulle helt enkelt bara skriva så här på slutet:
Okej, jag behöver alltså inte lägga till en period för ? När bör jag egentligen lägga till perioder?
Corokia cotoneaster skrev:Okej, jag behöver alltså inte lägga till en period för ? När bör jag egentligen lägga till perioder?
Jo det måste du. Och det har vi gjort båda två, men på lite olika sätt.
Alla sinus- (cosinus-/tangens- m.fl.) funktioner är periodiska.
Det betyder att du alltid måste lägga till en period när du löser ekvationer som innehåller sådana funktioner, om det inte uttryckligen anges att du bara ska hitta lösningar inom ett intervall som är mindre än perioden.
Yngve skrev:Corokia cotoneaster skrev:Okej, jag behöver alltså inte lägga till en period för ? När bör jag egentligen lägga till perioder?
Jo det måste du. Och det har vi gjort båda två, men på lite olika sätt.
Alla sinus- (cosinus-/tangens- m.fl.) funktioner är periodiska.
Det betyder att du alltid måste lägga till en period när du löser ekvationer som innehåller sådana funktioner, om det inte uttryckligen anges att du bara ska hitta lösningar inom ett intervall som är mindre än perioden.
Jaha, jag tänkte mer på om man ska få bort det negativa. Förstår du?:)
Corokia cotoneaster skrev:
Jaha, jag tänkte mer på om man ska få bort det negativa. Förstår du?:)
Aha, ja då förstår jag.
Hur man anger lösningsmängden handlar mycket om tycke och smak.
Själv föredrar jag uttrycket
framför
Detta för att jag tycker att det förstnämnda tydligare beskriver vilka vinklar som avses.
Men som sagt, det är en fråga om tycke och smak.
Yngve skrev:Corokia cotoneaster skrev:Jaha, jag tänkte mer på om man ska få bort det negativa. Förstår du?:)
Aha, ja då förstår jag.
Hur man anger lösningsmängden handlar mycket om tycke och smak.
Själv föredrar jag uttrycket
framför
Detta för att jag tycker att det förstnämnda tydligare beskriver vilka vinklar som avses.
Men som sagt, det är en fråga om tycke och smak.
Jaha okej!:) Då förstår jag! Tack så mycket :)



