20 svar

369 visningar

dajamanté är nöjd med hjälpen

Epic fail med både Jacobism och LALG

Problemet lyder:

1. Jag tänkte applicera vad jag lärde mig av AlvinB och Albiki, Jacobism:

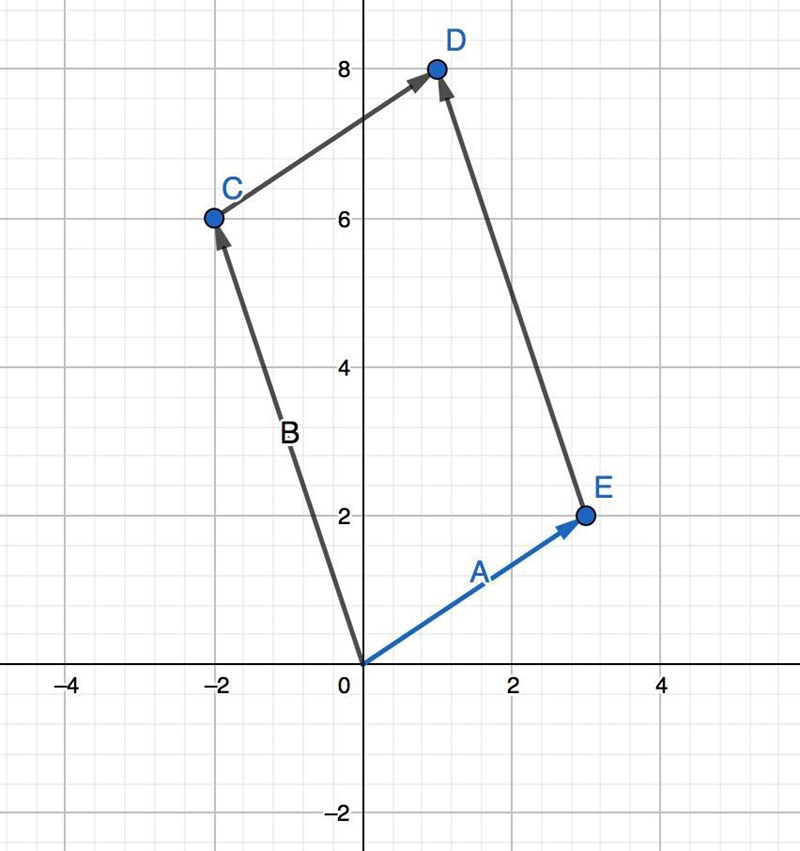
Området ser ut såhär:

$\iint_{D} 6 x + 2 y d x d y \to \iint u d u d v d (x, y) = \frac{d (x, y)}{d (u, v)} d u d v |\begin{matrix} \frac{d x}{d u} & \frac{d x}{d v} \\ \frac{d y}{d u} & \frac{d y}{d v} \end{matrix}| u = 6 x + 2 y y = v x = \frac{u}{6} - \frac{y}{3} = \frac{u}{6} - \frac{v}{3}$

$\frac{d x}{d u} = \frac{1}{6} \frac{d x}{d v} = - \frac{1}{3} \frac{d y}{d u} = 0 p . g . a d e t t a k o n s t i g t g r e j a t t v ä r e n k o n s t a n t f ö r u (? ? ?) \frac{d y}{d v} = 1$

J. det = $\dfrac{1}{6}$

$x$ evolverar mellan $\left[-2,3\right]$ . Gränserna är nog:

$6 \cdot - 2 + 2 y = 2 y - 12 = 2 v - 12$

$6 \cdot 3 + 2 y = 2 y + 18 = 2 v + 18$

Några av er huttrar av skräck och tänker ''Ser inte Daja att område är snett???"

Ja, det ser jag, därför försöker jag att sätta in en funktion; däremot blir den nästa integrering problematisk.

Men såhär har vi kommit:

$\int_{0}^{8} (\int_{2 y - 12}^{2 y + 18} u v d u) d v = \int_{0}^{8} {[\frac{u^{2}}{2}]}_{2 y - 12}^{2 y + 18} d v \int_{0}^{8} \frac{1}{2} [{(2 y + 18)}^{2} - {(2 y - 12)}^{2}] d v \int_{0}^{8} \frac{1}{2} [4 v^{2} + 4 \cdot 18 \cdot v + 18^{2} - 4 v^{2} + 4 \cdot 12 \cdot v - 12^{2}] d v \int_{0}^{8} \frac{1}{2} [4 v^{2} + 4 \cdot 18 \cdot v + 18^{2} - 4 v^{2} + 4 \cdot 12 \cdot v - 12^{2}] d v \int_{0}^{8} 2 [18 \cdot v + 9^{2} + 12 \cdot v - 6^{2}] d v = \int_{0}^{8} 2 [30 v - 45] d v 2 {[\frac{30 v^{2}}{2} - 45 v]}_{0}^{8} d v = 2 [\frac{30 \cdot 8^{2}}{2} - 45 \cdot 8] = [30 \cdot 8^{2} - 45 \cdot 4]$

Och detta är fel. Vad gick fel och var?

2. Och då försökte jag gräva upp gammal linjär algebra:

Den här:

Är egentligen två enhetsvektorer, $(\begin{matrix} 3 \\ 2 \end{matrix})$ och $(\begin{matrix} - 2 \\ 6 \end{matrix})$ i sitt eget koordinat system.

$(\begin{matrix} 3 & 2 \\ - 2 & 6 \end{matrix}) (\begin{matrix} u_{1} & u_{2} \\ v_{1} & v_{2} \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})$

Med mycket svett på pannan får jag inversmatrisen: $(\begin{matrix} \frac{3}{11} & \frac{- 1}{11} \\ \frac{1}{11} & \frac{3}{22} \end{matrix})$ , med vektor $u = (\begin{matrix} \frac{3}{11} \\ \frac{1}{11} \end{matrix})$ och $v = (\begin{matrix} \frac{- 1}{11} \\ \frac{3}{22} \end{matrix})$

Detta måste vara hur våra två vektor ser ut i en vanligt koordinatsystem $(\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})$ , eller (????)

Så nu istället för en konstigt parallelogram får vi en rektangel.

Jag försökt integrera:

$\int_{- \frac{1}{11}}^{\frac{3}{22}} (\int_{\frac{1}{11}}^{\frac{3}{11}} u v d u) d v \int_{- \frac{1}{11}}^{\frac{3}{22}} {[\frac{u^{2} v}{2}]}_{\frac{1}{11}}^{\frac{3}{11}} d v = \int_{- \frac{1}{11}}^{\frac{3}{22}} \frac{1}{2} {[u^{2} v]}_{\frac{1}{11}}^{\frac{3}{11}} d v = \int_{- \frac{1}{11}}^{\frac{3}{22}} \frac{1}{2} [\frac{8 v}{11^{2}}] d v \frac{4}{11} \frac{1}{2} {[v^{2}]}_{- \frac{1}{11}}^{\frac{3}{22}} = \frac{2}{11} [\frac{3}{22^{2}} - \frac{1}{11^{2}}]$

Som är inte rätt svar heller!

3. jag har försökt använda en kryssprodukt mellan vektorerna $u$ och $v$ , men när jag försöker få fram vinkel mellan dem här två blir det omedelbart något blodig:

$a r c \cos (\frac{u ∙ v}{|u| |v|}) = a r c \cos (\frac{6}{\sqrt{13 \cdot 40}})$ och det kan jag INTE utan miniräknare.

EDIT: nu har jag piggnat till och beräknat $\sin$ som:

$\sqrt{1 - \frac{6^{2}}{13 \cdot 40}} = \sqrt{\frac{484}{13 \cdot 40}}$

Kryssprodukten blir:

$\sqrt{\frac{484}{13 \cdot 40}} \cdot \sqrt{13} \sqrt{40} = \sqrt{484} = \sqrt{4 \cdot 121} = 22$ . Fortfarande inte rätt svar, men snällare på ögat.

Hej Daja, testa substitutionen

$u=6x+2y$

$v=-2x+3y$

Om du ritar in linjerna i området för några värden på u och v ser du något intressant? Vad blir gränserna i u och v?

Med jacobianen $|J|=\dfrac{1}{22}$ blir integralen

$\dfrac{1}{22}\int_0^{22} \int_0^{22} u\,dudv= \left[ \frac{u^2}{2} \right ]_0^{22}=242$

Guggle skrev:
Hej Daja, testa substitutionen
$u=6x+2y$
$v=-2x+3y$

Jag ser att linjer ser ut vinkelrätta mot var sin vektor, men varför är det så kan jag inte förklara. Hur tar man dot product på en linje?

Om du ritar in linjerna i området för några värden på u och v ser du något intressant? Vad blir gränserna i u och v?

Det vet jag inte :(

Med jacobianen $|J|=\dfrac{1}{22}$ blir integralen
$\dfrac{1}{22}\int_0^{22} \int_0^{22} u\,dudv= \left[ \frac{u^2}{2} \right ]_0^{22}=242$

Och det är såklart rätt svar... Men jag såg inte den intressanta grej...

Hej!

Integrationsområdet $D$ är en parallellogram vilket betyder att linjerna OE och CD har samma riktningsvektor (a) och att linjerna OC och ED har samma riktningsvektor (b). På vektorform skrivs ekvationen för linjen OE

$r=at$

och ekvationen för linjen CD är

$r=C+at$ .

På samma sätt är ekvationen för linjen OC

$r=bt$

och för linjen CD är den

$r=C+bt$ .

Detta kan användas för att skapa ett variabelbyte $(x,y)\to(u,v)$ som transformerar den sneda parallellogrammen i xy-planet till en axelparallell rektangel i uv-planet.

dajamanté skrev:
Guggle skrev:
Hej Daja, testa substitutionen
$u=6x+2y$
$v=-2x+3y$
Jag ser att linjer ser ut vinkelrätta mot var sin vektor, men varför är det så kan jag inte förklara. Hur tar man dot product på en linje?

Jag gjorde en jättefin Desmos-demonstation innan jag såg att du hade gjort en i geogebra, så du får leva med den istället :)

I demonstrationen är den röda linjen $u=6x+2y$ och den svarta linjen $v=-2x+3y$ .

Du kan testa att dra i reglagen och undersöka vilka punkter en given $(u,v)$ ger. Kommer vi åt alla punkter i området?

Metoden med variabelbyte handlar om att hitta ett smart byte som gör integralen enklare. Det kan handla om ett byte som gör själva integranden enklare. Men det kan också handla om ett byte som gör integrationsområdet enklare att komma åt.

I vårt fall är det naturligt att genast börja undersöka $u=6x+2y$ eftersom det är funktionen vi ska integrera. Dessutom är det linjer som är parallella med parallellogrammens ena basvektor. Men vi behöver också hitta en andra variabel, gärna en som inte ger några komplicerade uttryck. Ett smart val är då linjer som är parallella med parallellogrammens andra basvektor. Alltså väljer vi $(v=-2x+3y)$ .

Hej!

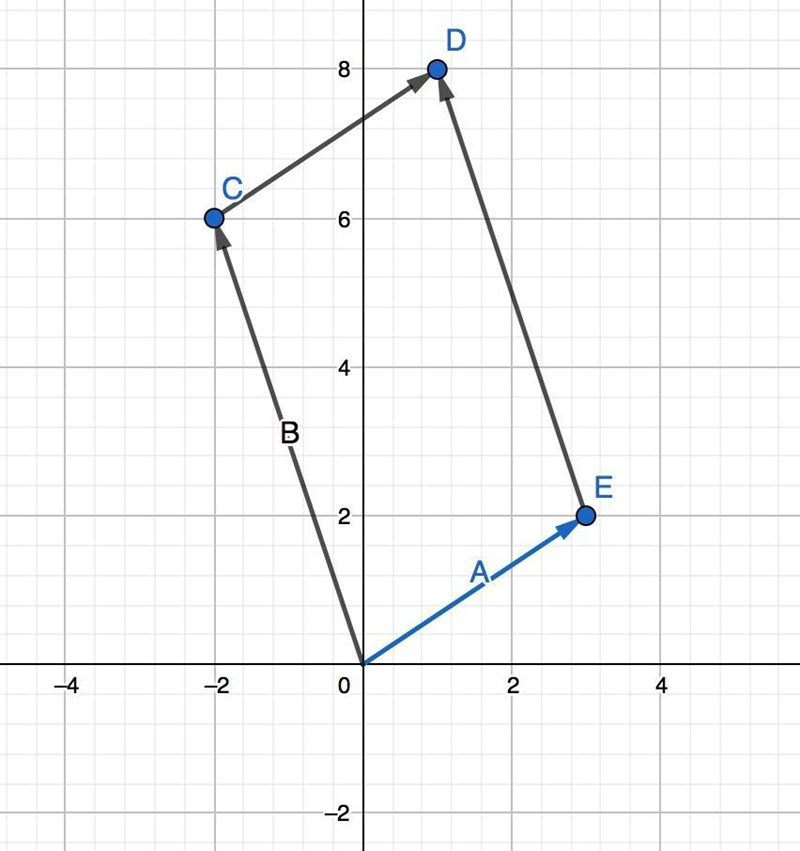
Riktningsvektorn för linjen OE är lika med $a = (3,2)$ och riktningsvektorn för linjen OC är lika med $b = (-2,6).$

På parameterform kan linjen OC skrivas

$\displaystyle \frac{x-0}{-2} = \frac{y-0}{6}\Leftrightarrow 6x+2y=0$

och ekvationen för den parallella linjen DE kan skrivas

$\displaystyle\frac{x-3}{-2} = \frac{y-2}{6}\Leftrightarrow 6x+2y=22$ .

På parameterform kan linjen OE skrivas

$\displaystyle \frac{x-0}{3} = \frac{y-0}{2}\Leftrightarrow 2x-3y=0$

och ekvationen för den parallella linjen CD kan skrivas

$\displaystyle\frac{x-(-2)}{3} = \frac{y-6}{2}\Leftrightarrow 2x-3y=-22$ .

Integrationsområdet kan skrivas

$\displaystyle D = \{(x,y):-22\leq 2x-3y\leq 0 \text{ och } 0 \leq 6x+2y \leq 22\} = \{(u,v) : -22 \leq u \leq 0 \text{ och } 0 \leq v \leq 22\} = D'$

där jag infört variabelbytet

$u = 2x-3y$ och $v = 6x+2y$ ,

som är ekvivalent med

$22x = 2u+3v$ och $22y = 2v-6u.$

Funktionaldeterminanten (Jacobianen) är lika med följande funktion.

$\displaystyle \frac{d(x,y)}{d(u,v)}=\left|\begin{matrix}\frac{2}{22} & \frac{3}{22}\\\frac{-6}{22}&\frac{2}{22}\end{matrix}\right| = \frac{1}{22^2}(2\cdot 2 - (-6)\cdot 3) = \frac{22}{22^2} = \frac{1}{22}$ .

Dubbelintegralen som ska beräknas kan därför skrivas på följande förenklade form.

$\displaystyle\iint_{D}(6x+2y)\,dxdy = \iint_{D'}v \cdot \frac{1}{22}\,dudv.$

Dubbelintegralen beräknas som två itererade enkelintegraler.

$\displaystyle\iint_{D'}v \cdot \frac{1}{22}\,dudv = \frac{1}{22}\cdot\int_{u=-22}^{0}\left\{\int_{v=0}^{22}v\,dv\right\}\,du=\frac{0-(-22)}{22}\cdot\frac{22^2-0^2}{2} = 11 \cdot 22 = 242.$

Den sökta dubbelintegralen är lika med

$\displaystyle\iint_{D}(6x+2y)\,dxdy = 242.$

Hej och tack🌷🌷!

Ok, nu åtminstone förstår jag vad det byggs på.

Guggle skrev:
Jag gjorde en jättefin Desmos-demonstation innan jag såg att du hade gjort en i geogebra, så du får leva med den istället :)

Den är jättefin och man ser dessa gränser noll till 22, för både $u,v$ !

Det är nåt grundläggande som jag inte är med i beräkningen av $\left|J\right|$ .

Visst gör vi en $|\begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix}|$ ?

Isf, med $u = 6 x + 2 y$ och $v = - 2 x + 3 y$ , har vi inte:

$x = \frac{u}{6} - \frac{y}{3} y = \frac{u}{2} - 3 x x = \frac{3 y}{2} - \frac{v}{2} y = \frac{v}{2} - \frac{2 x}{3}$

Detta ger mig:

$|\begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix}| = |\begin{matrix} \frac{1}{6} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{3} \end{matrix}| = \frac{11}{36}$

Albiki skrev:
där jag infört variabelbytet
u=2x−3yu=2x-3y och v=6x+2yv=6x+2y,
som är ekvivalent med
22x=2u+3v22x=2u+3v och 22y=2v−6u.

Jag är inte van med parametrisering av linjer såhär men jag förstår. Däremot detta ekvivalens är jag inte med direkt.

Samma för din $|J|$ beräkningen, varför tog du $=22$ och inte $=0$ ?

dajamanté skrev:

Isf, med $u = 6 x + 2 y$ och $v = - 2 x + 3 y$ , har vi inte:
$x = \frac{u}{6} - \frac{y}{3} y = \frac{u}{2} - 3 x x = \frac{3 y}{2} - \frac{v}{2} y = \frac{v}{2} - \frac{2 x}{3}$

Nä, nu Dajaslarvade du när du löste ut x- och y. För att kunna derivera enkelt måste du uttrycka dem i u och v, dvs $x(u,v)$ och $y(u,v)$ . Annars måste du ta hänsyn till att även y beror av u när du plockar fram den partiella derivatan till x osv. Gör alltså så här:

Om du nu bildar funktionaldeterminanten får du förhoppningsvis rätt!

Och nu tänker jag visa en genväg. Du behöver inte lösa ut x,y, istället kan du derivera u och v partiellt med avseende på x och y och använda att

Inversens funktionaldeterminant är lika med det inverterade värdet av funktionens funktionaldeterminant.

Så här:

$\begin{vmatrix} \frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x} &\frac{\partial v}{\partial y} \end{vmatrix}=\begin{vmatrix} 6& 2\\ -2 &3 \end{vmatrix}=18+4=22$

Och nu är alltså absolutbeloppet av J det inverterade värdet, $|J|=\dfrac{1}{22}$

Like magic!

Guggle skrev:
Nä, nu Dajaslarvade du när du löste ut x- och y. För att kunna derivera enkelt måste du uttrycka dem i u och v, dvs $x(u,v)$ och $y(u,v)$ . Annars måste du ta hänsyn till att även y beror av u när du plockar fram den partiella derivatan till x osv. Gör alltså så här:

Oh...

Oooh!

Jag vet inte om jag D-slarvade eller om jag hade ingen aning om hur det funkade.

Grubblar till sig själv: *Gjorde vi också det i den andra problem? Ja, det gjorde vi nog, men $y=v$ då så jag märkte ingenting....*

Om du nu bildar funktionaldeterminanten får du förhoppningsvis rätt!

Det ska vi se imorgon, nu börjar dagens programmeringstimme :)

Inversens funktionaldeterminant är lika med det inverterade värdet av funktionens funktionaldeterminant.

Trots att den här mening är mystisk, när jag såg din demonstration måste jag erkänna att the magic is strong with this one!!

Guggle skrev:
Nä, nu Dajaslarvade du när du löste ut x- och y. För att kunna derivera enkelt måste du uttrycka dem i u och v, dvs $x(u,v)$ och $y(u,v)$ . Annars måste du ta hänsyn till att även y beror av u när du plockar fram den partiella derivatan till x osv. Gör alltså så här:
Om du nu bildar funktionaldeterminanten får du förhoppningsvis rätt!
Och nu tänker jag visa en genväg. Du behöver inte lösa ut x,y, istället kan du derivera u och v partiellt med avseende på x och y och använda att
Inversens funktionaldeterminant är lika med det inverterade värdet av funktionens funktionaldeterminant.
Så här:
$\begin{vmatrix} \frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x} &\frac{\partial v}{\partial y} \end{vmatrix}=\begin{vmatrix} 6& 2\\ -2 &3 \end{vmatrix}=18+4=22$
Och nu är alltså absolutbeloppet av J det inverterade värdet, $|J|=\dfrac{1}{22}$
Like magic!

Okej. Det blev rätt.

Men kan vi prata lite mer on linjär algebra?

Vi har två vektorer:

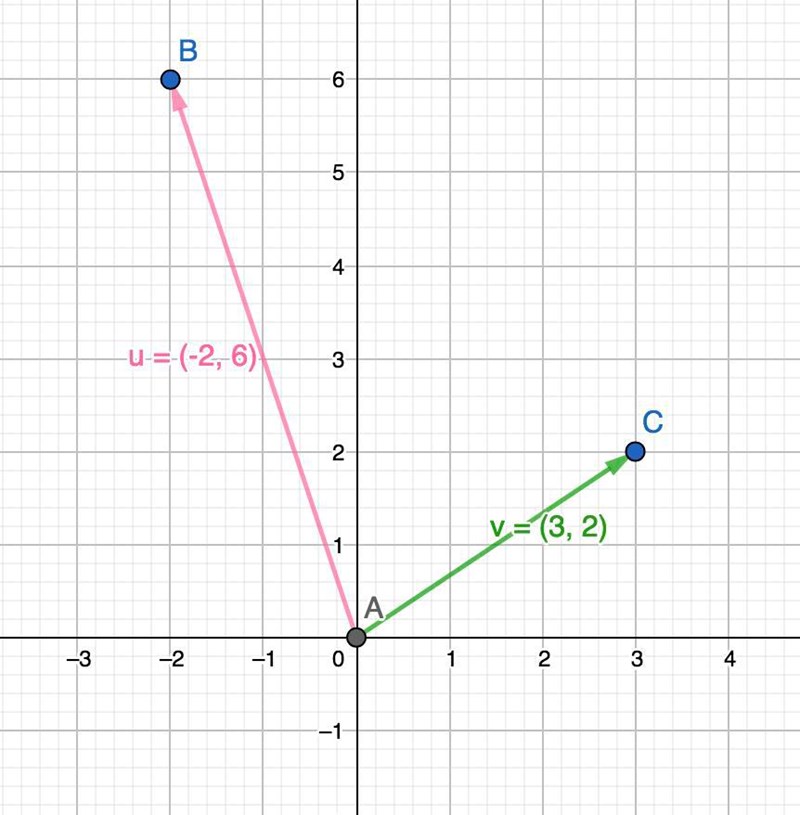
Determinanten mellan dem två ger oss värden = 22. Det är vår fält.

Nu måste vi föreställa oss att vi har funktionen $6x+2y$ som vi måste integrera över fältet.

Enligt integralkalkylmedelvärde satsen har vi:

Om f är en kontinuerlig funktion på det slutna intervallet [a,b], så finns en punkt c i [a,b] sådan att

$\int_a^bf(t)\,dt=f(c)(b-a)$

Värdet $f(c)$ i satsen är funktionens medelvärde på intervallet. I vårt fall har vi en förstagrad kontinuerligt funktion som på intervallet antar max värde 22. Medelvärden blir 11.

Kan vi i detta fall bestämma att lösningen är:

$22 \cdot 11 = 242$ ?

dajamanté skrev:

Men kan vi prata lite mer on linjär algebra?
Determinanten mellan dem två ger oss värden = 22. Det är vår fält.

Nu måste vi föreställa oss att vi har funktionen $6x+2y$ som vi måste integrera över fältet.

Ja, eftersom funktionen är linjär och dess nivåkurvor är parallella med en av basvektorerna kan vi använda en sådan metod för att bestämma integralen. Detta beror på att det är extra lätt att bestämma medelvärdet av funktionens värde i området.

Enligt integralkalkylmedelvärde satsen har vi:
Om f är en kontinuerlig funktion på det slutna intervallet [a,b], så finns en punkt c i [a,b] sådan att
$\int_a^bf(t)\,dt=f(c)(b-a)$

Värdet $f(c)$ i satsen är funktionens medelvärde på intervallet. I vårt fall har vi en förstagrad kontinuerligt funktion som på intervallet antar max värde 22. Medelvärden blir 11.

Ja, det är ungefär så det fungerar, fast i två dimensioner. Kraven är att funktionen $f(x,y)$ ska vara kontinuerlig (eller iallafall snäll) på ett kompakt område D (också snällt, t.ex. kvadrerbart). Arean $A$ av området är

$\displaystyle A=\iint_D\, dxdy$

I det här fallet har du använt dina ninjakunskaper i linjär algebra för att bestämma arean $A$ .

Om vi förutsätter att $f(x,y)$ är snäll (inte gör elaka saker i området) finns det två reella tal, $f_{min}$ och $f_{max}$ , sådana att

$f_{min}\leq f(x,y)\leq f_{max}$

Alltså gäller (med arean $A$ )

$\displaystyle Af_{min}\leq \iint_D f(x,y)\, dxdy \leq Af_{max}$

Vi drar slutsatsen att Integralens värde $I$ delat med A måste höra till det slutna intervallet $[f_{min}, f_{max}]$ .

Om vi förutsätter att området D är bågvis sammanhängande finns det enligt satsen om mellanliggande värden en punkt $(a,b)$ sådan att

$f(a,b)=\dfrac{I}{A}$

Detta kallas ofta medelvärdessatsen för integraler eftersom kvoten $\frac{I}{A}$ är medelvärdet av funktionen $f(x,y)$ då $(x,y)\in D$ .

Varför använder man inte det jämnt då?

För att det oftast är väldigt svårt att veta exakt i vilken/vilka punkt(er) funktionen f(x,y) antar sitt medelvärde. I i just detta fall ligger medelvärdet på mitten eftersom funktionen är linjärt växande.

Till Guggle:

Vad betyder det att en funktion $f : \mathbb{R}^2 \to \mathbb{R}$ är linjärt växande?

Detta behöver väl en slags ordningsrelation på $\mathbb{R}^2$ , så att man kan avgöra när en punkt $(a,b)$ är "mindre än" en punkt $(x,y)$ ?

Albiki skrev:
Till Guggle:
Vad betyder det att en funktion $f : \mathbb{R}^2 \to \mathbb{R}$ är linjärt växande?

Ja, det var lite dumt uttryckt av mig i hastigheten. Naturligtvis menade jag inte att funktionen $f(x,y)$ är växande i största allmänhet. Vad jag menade är att funktionen växer linjärt utmed parallellogrammens basvektor $(3,2)$ eftersom funktionens gradient är en konstant vektor.

Det är enkelt att dela parallellogrammen i två lika stora delar med en symmetrilinje (den röda linjen mitt i området). Eftersom funktionen växer linjärt (utmed basvektorn) är värdet på nivåkurvan längs den röda linjen av symmetri också funktionens medelvärde för hela området:

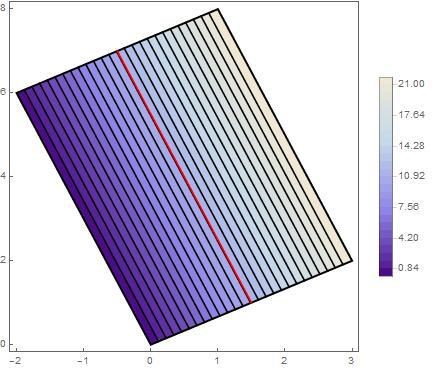
$f(0,0)+\frac{|\tau|}{2}\frac{\partial f}{\partial \tau}=\frac{|\tau|}{2}(\hat{\tau}\cdot\nabla f)=\frac{1}{2}(6,2)\cdot (3,2)=11$

Arean av området är 22 och därmed är värdet av integralen $11\cdot 22=242$ .

Hej!

Angående diskussionen om Medelvärdessatsen:

Dubbelintegralen $\iint_{D'}v\cdot\frac{1}{22}\,dudv$ kan också beräknas som den itererade integralen

$\displaystyle \int_{v=0}^{22}\left\{\frac{1}{22}\int_{u=-22}^{0}v\,du\right\}\,dv$

I den inre integralen är $v$ lika med en konstant, och medelvärdet för den konstanta funktionen $g_{v}(u) = v$ över intervallet $-22 < u=""><>$ är lika med

$\displaystyle \bar{g}_{v}\equiv \frac{1}{22} \int_{-22}^{0}g_{v}(u)\,du = v.$

Dubbelintegralen kan alltså beräknas som summan av alla dessa medelvärden

$\displaystyle\int_{v=0}^{22}\bar{g}_{v}\,dv =\int_{v=0}^{22}v\,dv = \frac{22^2}{2} = 11 \cdot 22 = 242.$

Slutsats: Allt detta prat om att använda Medelvärdessatsen i denna tråd är inget annat än egenskapen att byta integrationsordning i en dubbelintegral. Detta resultat kallas Fubinis sats.

Albiki skrev:
Slutsats: Allt detta prat om att använda Medelvärdessatsen i denna tråd är inget annat än egenskapen att byta integrationsordning i en dubbelintegral. Detta resultat kallas Fubinis sats.

Nej, tanken med allt detta prat är insikten att om vi känner till medelvärdet av en funktion eller lätt kan beräkna det genom t.ex. tyngdpunktsberäkning eller något annat symmetriargument behöver vi bara multiplicera detta medelvärde med arean (eller volymen) av hela integrationsområdet för att få integralens värde.

Börjar man fundera över integrationsordning och/eller eventuella variabelbyten kan man lika gärna räkna ut integralen.

Medelvärdet av $f(x,y)$ i hela parallellogrammen är 11. Arean av hela parallellogrammen är 22. Alltså blir integralen $11\cdot 22=242$ .

Jaha..., så det du vill få Daja att inse är att $2 \cdot (\frac{3 + 5}{2})$ är samma sak som $3+5$ .

Guggle skrev massor och avslutade med:

....
Varför använder man inte det jämnt då?
För att det oftast är väldigt svårt att veta exakt i vilken/vilka punkt(er) funktionen f(x,y) antar sitt medelvärde. I i just detta fall ligger medelvärdet på mitten eftersom funktionen är linjärt växande.

Tack och sorry för sent svar.

Det är den här tiden av åren där vi har härligt semester med familjen och där vi alla har fullt upp med varan och kan inte /ignorera_alla. Tyvärr.

Men men, jag förstår allt!

Jag trodde att det var jag som var dålig på den medelvärdesatsen förutom när den var mycket snäll och linjär, första grand funktionsberoende. Men egentligen om vi har en ormig och mycket kurvig funktion går det inte alls helt enkelt!

Härligt volym förresten!

Albiki skrev:
Jaha..., så det du vill få Daja att inse är att $2 \cdot (\frac{3 + 5}{2})$ är samma sak som $3+5$ .

Nej, jag tolkade det som att Daja löst problemet och nu var intresserad av genvägar baserade på linjär algebra och medelvärdesegenskaper. Hon verkar använda det man brukar kalla integralkalkylens medelvärdessats i en variabel. Jag visade då hur man härleder motsvarande medelvärdessats i flera variabler och nämnde något om vilka krav det ställer på området och funktionen. Jag påpekade också att det kanske inte är trivialt för alla att medelvärdet av funktionen är 11 och beskrev hur man kan hitta medelvärdet utan att använda integraler.

Det här är frågan jag försöker besvara:

dajamanté skrev:
Men kan vi prata lite mer on linjär algebra?
Determinanten mellan dem två ger oss värden = 22. Det är vår fält.
Om f är en kontinuerlig funktion på det slutna intervallet [a,b], så finns en punkt c i [a,b] sådan att
∫baf(t) dt=f(c)(b−a)

Värdet f(c)
i satsen är funktionens medelvärde på intervallet. I vårt fall har vi en förstagrad kontinuerligt funktion som på intervallet antar max värde 22. Medelvärden blir 11?

Guggle ritade massor konstiga symboler från den gamla Egyptiska riket med en ännu snyggare figur:
....
$f(0,0)+\frac{|\tau|}{2}\frac{\partial f}{\partial \tau}=\frac{|\tau|}{2}(\hat{\tau}\cdot\nabla f)=\frac{1}{2}(6,2)\cdot (3,2)=11$
Arean av området är 22 och därmed är värdet av integralen $11\cdot 22=242$ .

Gymnasiematte tolkning:

Med simmetrilinjen och lika stora delar, du menar att mitt värdet kan tas med dem två vektor som korsas mitt i parallelogram?

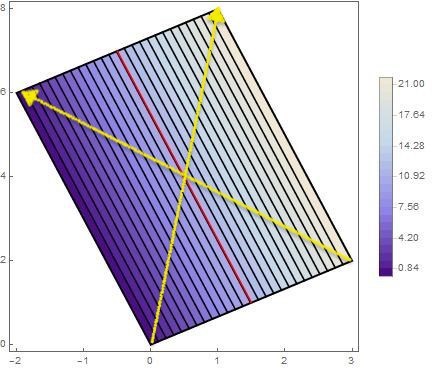
Som tas fram med:

$- \frac{4}{5} x + \frac{22}{5} = 8 x x = \frac{1}{2}, y = 4 6 x + 2 y = 11$

Eller linjen som är precis mitt i mellan $y = - 3 x$ och $y = - \frac{4}{5} x + \frac{22}{5}$ ...

Albiki skrev:
Jaha..., så det du vill få Daja att inse är att $2 \cdot (\frac{3 + 5}{2})$ är samma sak som $3+5$ .

Jag är bara tacksam för allt tid Guggle och digsjälv lägger på att hjälpa mig förstå sambandet mellan alla dessa sats.

Guggle skrev:
Albiki skrev:
Jaha..., så det du vill få Daja att inse är att $2 \cdot (\frac{3 + 5}{2})$ är samma sak som $3+5$ .
Nej, jag tolkade det som att Daja löst problemet och nu var intresserad av genvägar baserade på linjär algebra och medelvärdesegenskaper.

*jag vet att detta är inte till mig men*

Ja, det är precis det jag var efter!

Sedan du skrev i den andra posten att arean kan beräknas med kryssprodukten insåg jag att vi kunde lösa vår problem med linjär algebra, särkilt i denna fall med en snäll integrations area och en snäll växande funktion.

Hon verkar använda det man brukar kalla integralkalkylens medelvärdessats i en variabel.

Jo alltså jag visste inte att det var i en variabel, jag litade på Wikipedia...

Jag visade då hur man härleder motsvarande medelvärdessats i flera variabler och nämnde något om vilka krav det ställer på området och funktionen. Jag påpekade också att det kanske inte är trivialt för alla att medelvärdet av funktionen är 11 och beskrev hur man kan hitta medelvärdet utan att använda integraler.

Och jag tackar för det, jag ska definitivt dra ut detta kort om det blir svårigheter på provet...

Svara Avbryt

Visa senaste svar