Fel vid skapande av cosinusserie!
Tjena!
Kommer nästan hela vägen till mållinjen när jag ska ta fram fourierserien till en funktion på trigonometrisk form (se bild nedan för mina beräkningar). Men där det tar stopp är alldeles på slutet när jag ska sätta samman mitt a_0 och a_n. Varför får de ett annat svar än mig? Jag begriper mig varken på vad min lärare skrivit i lösningen eller varför de får det de får. Tänkte det kanske var en omskrivning av vad jag redan räknat fram, men misslyckas se något.
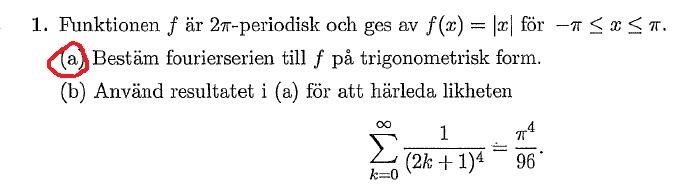

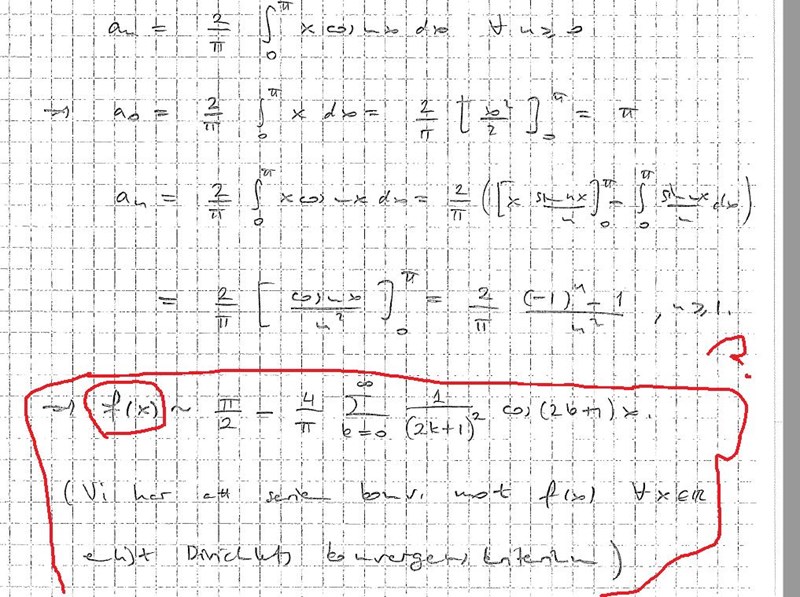

Det jag markerar med fingret är själva formeln jag utgår ifrån när jag skapar min fourierserie för uttrycket ifråga.
Det rödmarkerade i min lösning är cosinusserien jag får ihop men tydligen stämmer det inte.
Tacksam för svar!
/Shawn
Hej!
Funktionens fourierserie är
och din funktion är jämn vilket betyder att fourierserien också är jämn så samtliga sinustermer i serien är lika med noll. Funktionens fourierserie är därför
där fourierkoefficienterna är sådana att
Albiki skrev:Hej!
Funktionens fourierserie är
och din funktion är jämn vilket betyder att fourierserien också är jämn så samtliga sinustermer i serien är lika med noll. Funktionens fourierserie är därför
där fourierkoefficienterna är sådana att
köper det du skriver om att vi kan försumma sinus termen, so far so good.
Men vad i all sin dagar har den sista raden du skrev för koppling med uttrycket de får fram (det rödmarkerade 3:e bilden)? Speciellt i och med att de får k-termer i sitt uttryck och det gör mig riktigt förvirrad.
Integralerna beräknas med partiell integration.
För den första integralen är och varför
och den andra integralen använder och som ger
.
Addera de två integralerna (notera minustecknet hos den första integralen) för att få fourierkoefficienterna
Notera att när är ett jämnt tal och när är ett udda tal, varför när är jämnt tal och när är udda tal.
Fourierserien är därför
Hej!
Albiki har löst det väldigt noggrant, men bara för att snabbt besvara din fråga:
Notera att din täljare är lika med noll då n är jämnt, därför är serien ekvivalent med dess "udda" serie (då alla termer då n är jämn blir noll), och därför kan du sätta . Därefter följer likheten mellan serierna direkt: din täljare är därmed alltid lika med -2 (bryt ut det och du får ) och gör substitutionen som jag nämnde ovan. Sedan är din serie lika med facits.
Om man tillämpar Parsevals formel för funktionen där fås
Med när är udda (och noll när är jämn) producerar Parceval resultatet
Med ger resulterar Parcevals formel i serien

