Fjäderförlängning

Hej! Försöker beräkna denna uppgift men kommer ingenstans.
Vad är det man ska använda:
- Svängningsekvationen?
- Energiprincipen?
Har försökt med båda men kommer ingen vart. Tacksam för svar!
Rita en bild som illustrerar vad som händer.
Ställ upp Newton II för partikeln. Uppgiften handlar om rotation / centripetalkraft. Kan du några samband? Vad måste gälla för att partikeln ska hållas kvar i sin bana?
Uppgiften innehåller en fjäder. Kommer du ihåg något samband mellan kraft och fjäderförlängning?
D4NIEL skrev:Rita en bild som illustrerar vad som händer.
Ställ upp Newton II för partikeln. Uppgiften handlar om rotation / centripetalkraft. Kan du några samband? Vad måste gälla för att partikeln ska hållas kvar i sin bana?
Uppgiften innehåller en fjäder. Kommer du ihåg något samband mellan kraft och fjäderförlängning?
Jag tänker att man kan använda cylinderkoordinater på något sätt men får det inte att fungera.
För att partikeln ska hållas kvar i sin bana måste väl accelerationen i radiell riktning ut mot fjädern vara 0?
Ja det finns ju svängningsekvationen och F = -kx ?
I uppgiften står det att rotationen sker i en cirkelbana med konstant hastighet . Vi får anta att det sker med konstant radie i dynamisk jämvikt utmed den glatta ytan, dvs ingen höjd eller gravitation inblandad.
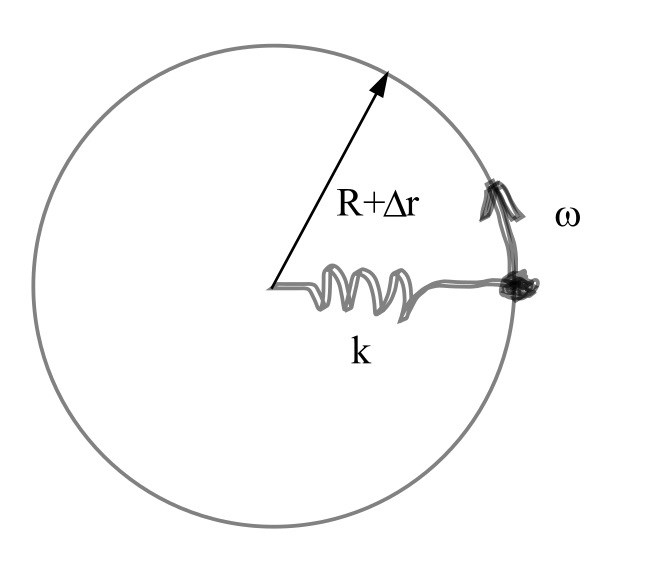 För att massan ska följa cirkelbanan måste den accelereras i radiell led och redan på gymnasiet lärde vi oss att .
För att massan ska följa cirkelbanan måste den accelereras i radiell led och redan på gymnasiet lärde vi oss att .
Men du kan också härleda den genom att använda cylinderkoordinater, då är lägesvektorn
I det sista steget utmyttjade vi att
Deriverar vi ytterligare en gång med avseende på t får vi
Där vi återigen utnyttjade att
Nu ställer vi upp Newtons andra lag i radiell led:
D4NIEL skrev:I uppgiften står det att rotationen sker i en cirkelbana med konstant hastighet . Vi får anta att det sker med konstant radie i dynamisk jämvikt utmed den glatta ytan, dvs ingen höjd eller gravitation inblandad.
För att massan ska följa cirkelbanan måste den accelereras i radiell led och redan på gymnasiet lärde vi oss att .
Men du kan också härleda den genom att använda cylinderkoordinater, då är lägesvektorn
I det sista steget utmyttjade vi att
Deriverar vi ytterligare en gång med avseende på t får vi
Där vi återigen utnyttjade att
Nu ställer vi upp Newtons andra lag i radiell led:
Tack så mycket. Hade glömt att radien förändras och inte är konstant, därför man får R + delta(r). Tack!


