Flervariabel, jobbig uppgift
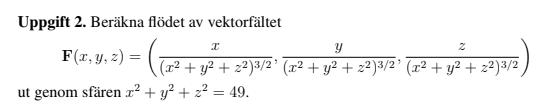
Jag har beräknat denna, till hjälp hade jag en liknande uppgift där skillnaden var att de hade ett klot istället för en sfär som gavs som: .
Som vissa kanske ser direkt så går det inte att använda gauss sats utan det krävs en lite annan metod där man delar upp sfären i en övre och undre halva osv. Mycket beräkningar ligger bakom men jag undrar iallafall om någon kanske kan se direkt ifall jag gjort rätt för jag misstänker att det faktum att det är ett klot på den andra uppgiften inte gör någon skillnad. Men radien är ju annorlunda, men när jag gör min beräkning så tar många av siffrorna ut sig efter att jag beräknat sista integralen och jag blir kvar med samma flöde som sfären med radie 1. Känns ologiskt, borde inte en större sfär ha ett större flöde? Jag får iallafall som totalt flöde och det får även de. Finns det någon som direkt kan säga att nej sfärens storlek påverkar inte det totala flödet eller nått i den stilen, eller har jag gjort något fel? Kan det vara så att vektorfältet i denna uppgift är speciellt för den påverkas ju av sfärens storlek då man subsituterar z osv?
Vektorfältet blir mindre krångligt i sfäriska koordinater.
Väljer vi flödet ut ur en sfär med radien får vi alltså ()
Oberoende av .
Flödet är detsamma för alla omslutande ytor eftersom divergensen i mellanliggande område är noll. Vi har bara en punktkälla i origo.
D4NIEL skrev:Vektorfältet blir mindre krångligt i sfäriska koordinater.
Väljer vi flödet ut ur en sfär med radien får vi alltså ()
Oberoende av .
Flödet är detsamma för alla omslutande ytor eftersom divergensen i mellanliggande område är noll. Vi har bara en punktkälla i origo.
Ah okej tack. Så det är alltså så som jag misstänkte att radien inte spelar roll. Kan man rent informellt säga att ifall ett vektorfälts divergens är =0 så kommer kroppen eller området den verkar på att ha samma flöde oavsett storlek på området, eller råkar det bara gälla för detta område eller vektorfält specifikt?
I alla områden där divergensen är 0 blir flödet 0. Nu var poängen här att det inte är 0 i 0, så områden runt origo kommer inte vara 0. Men alla andra bitar du lägger till ditt område är helt ointressanta.
Micimacko skrev:I alla områden där divergensen är 0 blir flödet 0. Nu var poängen här att det inte är 0 i 0, så områden runt origo kommer inte vara 0. Men alla andra bitar du lägger till ditt område är helt ointressanta.
Jaha okej då fattar jag, tack👍
Kan man säga attt divergensen fungerar som nån skalfaktor för ett område men jag kanske tänker fel. Till exempel om vi har ett vektorfält med divergens 1 så ökar flödet linjärt med radien på sfären


