Flervariabelanalys, mystisk mängd
Jag har en uppgift där jag sak rita ut .
Jag delar upp absolutbeloppet i:
Randen till dessa ges ju då av:
Sedan vet vi ju att när . Så innebär det allt "ovanför" den linjen vilket är logiskt.
Men för bör ju det rimligen tolkas också som allt ovanför den linjen men det gör den inte. Mängden tolkas som allt under den linjen trots att y ska vara större än -2-x.
För förtydligande, jag tolkar mängden som 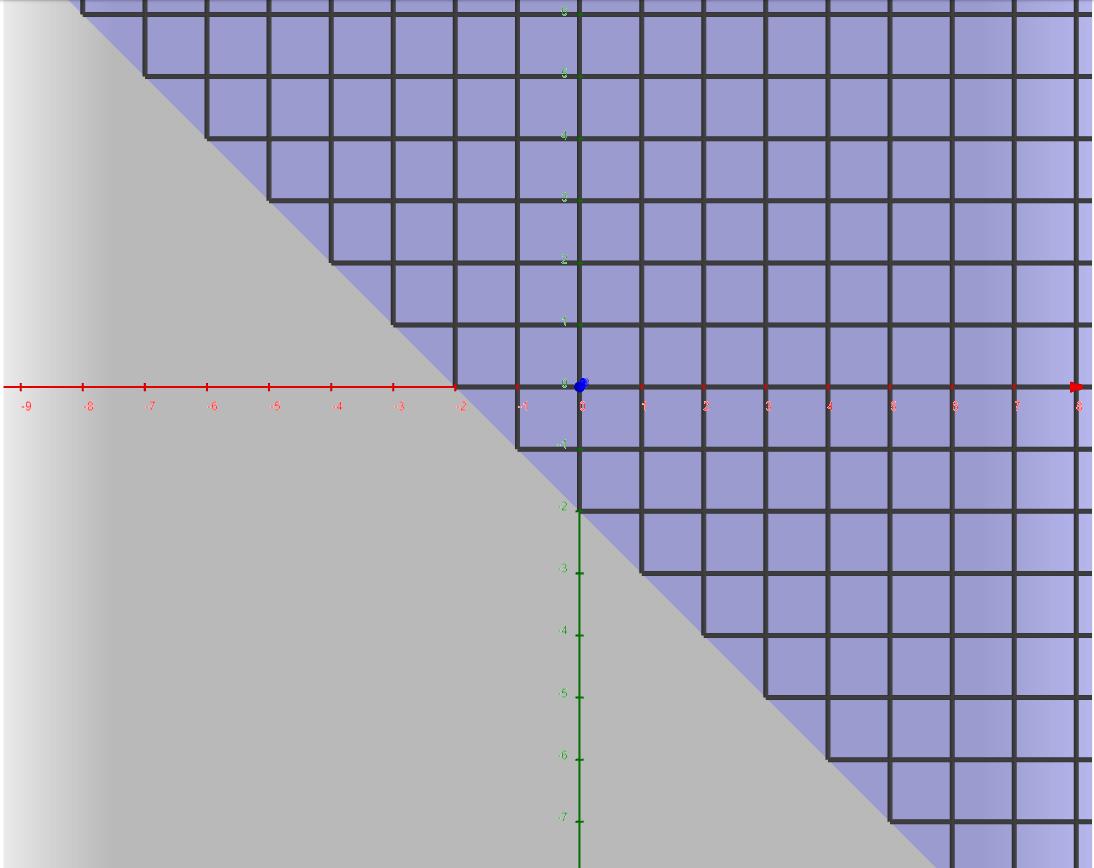
Men den rätta mängden är: 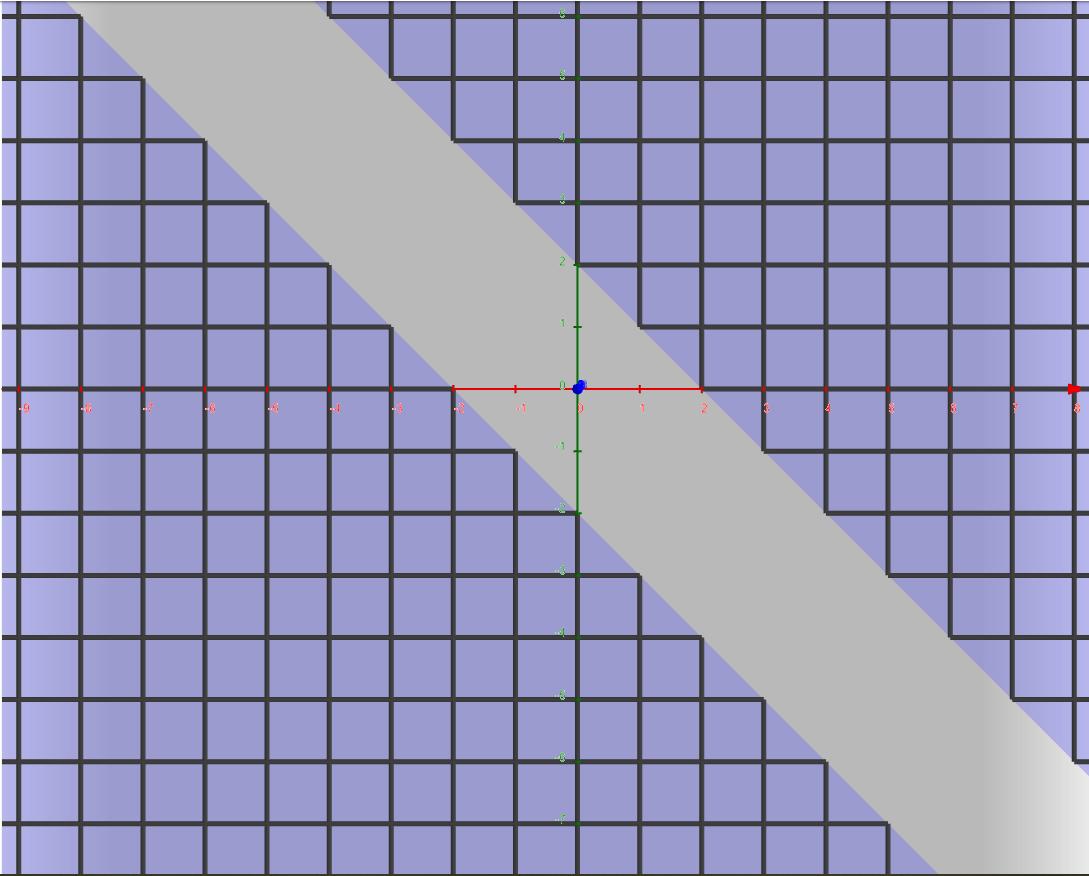
Varför stämmer inte det som jag tänker?
Absolutbeloppet kan ersättas av antingen eller
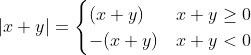
D4NIEL skrev:Absolutbeloppet kan ersättas av antingen eller
Det är ju det jag gjort.
Men det blir ju endå fel mängd för y>-2-x verkar inte vara rätt mängd däremot verkar y>2-x vara det. Det är det som är skumt menar jag.
Freedom hold skrev:D4NIEL skrev:Absolutbeloppet kan ersättas av antingen eller
Det är ju det jag gjort.
Men det blir ju endå fel mängd för y>-2-x verkar inte vara rätt mängd däremot verkar y>2-x vara det. Det är det som är skumt menar jag.
Vid en likhet "=" kan du flytta över minustecknet utan att tänka. Men när du har en olikhet ">=" så måste du byta håll på olikheten.
Enkelt exempel:
-1<5 om jag multiplicerar båda sidor med -1 så får jag 1 och -5 men nu måste olikheten byta håll. 1>-5.
Så x+y>=-2 är fel. Du har -(x+y)>=2. Sedan vill du multiplicera båda sidor med minus 1. Men då måste du byta håll på olikheten.
Egocarpo skrev:Freedom hold skrev:D4NIEL skrev:Absolutbeloppet kan ersättas av antingen eller
Det är ju det jag gjort.
Men det blir ju endå fel mängd för y>-2-x verkar inte vara rätt mängd däremot verkar y>2-x vara det. Det är det som är skumt menar jag.
Vid en likhet "=" kan du flytta över minustecknet utan att tänka. Men när du har en olikhet ">=" så måste du byta håll på olikheten.
Enkelt exempel:
-1<5 om jag multiplicerar båda sidor med -1 så får jag 1 och -5 men nu måste olikheten byta håll. 1>-5.
Så x+y>=-2 är fel. Du har -(x+y)>=2. Sedan vill du multiplicera båda sidor med minus 1. Men då måste du byta håll på olikheten.
Aha okej man måste byta olikhet då fattar jag! tack!
D4NIEL skrev:Absolutbeloppet kan ersättas av antingen eller
Gäller skiftet av olikhet även ifall vi har eller .
Dvs när termerna innanför absolutbeloppsstecknet endast kan anta postiva värden?
Om du skulle ställa upp det likadant skulle du få vad som gäller när x2+y2<0 i undre raden, och det kommer aldrig hända så det tillför ingenting. x2-y2 kan bli negativt.



