Fluiddynamik - hur beräknar författarna dubbelintegralen?

Det är nog tänkt att man har gjort ansatsen $\overrightarrow{v}\left(\overrightarrow{r}\right)=v_x\left(r\right){\overrightarrow{e}}_x$.

Jag är delvis med. Beror inte hastigheten också på vinkeln? Jag är med på att $\mathbf{v} \cdot \mathbf{n}=-v_x$ vid den första ytan och $\mathbf{v} \cdot \mathbf{n}=v_x$ vid den andra.

De är nog inte tänkt att behandla ett allmänt fall utan ett enkelt specialfall från vilket man kan dra vissa slutsatser. Det är ju ett cylindersymmetriskt stationärt problem så det är rimligt att anta cylindersymmetri hos hastighetsfältet.

Vad betyder det att hastighetsfältet har cylindersymmetri? Att hastigheten är samma för varje $r$, oavsett $\theta$?

Ja, oberoende av $\theta$. Om du vrider röret en vinkel kring x-axeln så ser det fortfarande likadant ut.

De skulle naturligtvis ha sagt vilka antaganden man gjort, men i fysikböker är man inte alltid så explicit med sådant.

Okej, det förklarar en del i alla fall. Men jag är ändå inte riktigt med på vad som händer. Låt oss studera den första ytan där fluiden kommer in, kalla den $A_1$. I så fall har vi:

$\displaystyle -\rho\iint_{A_1}v^2_x\left(r\right)dA_1$

Hur gör de sedan för att faktiskt få ut värdet på den här integralen? Det är inte uppenbart för mig varför detta ska bli $-\rho v^2_x 2\pi r\Delta r$. Detta blir det väl bara i det väldigt speciella fallet där $v_x$ inte har beroende på $r$ heller?

Man tänker sig nog att delta-r är så litet (dr) att v_x inte hinner variera nämnvärt mellan r och r + delta-r.

Är integralen verkligen rätt objekt att använda i så fall? Det verkar ju som vi får något "differentiellt" (infinitesimalt) men en integral ger ju i regel något reellt. Är det med andra ord notationsmissbruk (notationsmisshandel) från författarna?

Du kan tänka att det är en tillämpning av medelvärdessatsen. Dvs att det skall stå v_x(r*) där r* är ett värde mellan r och r + delta-r, om du vill vara mer matematiskt rigorös.

Jag vet inte om rigör är mitt problem för tillfället. Jag fattar inte vad de gör överhuvudtaget... Tydligen mycket man bara ska förstå utan att de ska behöva bemöda sig med att beskriva det.

Nu har jag sovit på saken men jag är fortfarande ganska lost. Har man bara tänkt att $v_x$ är konstant över båda ytorna, så att $v_x$ inte har något beroende på $r$ eller $\theta$ alls? I så fall borde ju $v_x$ vara lika stor i hela fluiden eftersom det tydligen ska gälla att "the velocity profile does not vary along the axis of flow."

Det är nog tänkt att v_x varierar med r. Annars blir det svårt att uppnå no-slip-villkoret vid rörytorna. Men den sista meningen säger att man antar att v_x är oberoende av x-koordinaten. v_x = v_x(r).

Jag menar inom den mindre kontrollvolymen man studerar, det man kallar för en "circular conduit". Antar man konstant hastighet över ytorna där eller antar man även där variation över ytorna?

Så som de har beräknat integralen har de ju skrivit det som om $v_x$ inte beror på $r$ eller $\theta$ inom de små kontrollytorna (och därför kan faktorisera ut $v_x$) från varje ytintegral men beror på $x$ (eftersom de har subscripten ${|}_{x+\Delta x}$ etc.)

Ja. Man tänker sig att delta-r är litet så att v_x är nästan konstant den lilla ytan. Det antagandet blir naturligtvis mer korrekt ju mindre vi gör delta-r.

Jag tror att jag har fundamentalt missförstått figuren. Vilka ytor är det som utgör kontrollytorna? Jag tolkade det som att det vore:

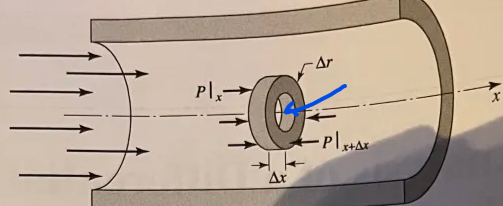
Alltså de vita öppningarna som omsluts av ringen. Är det själva ringens ytor, alltså det som är skuggat i figuren, som är kontrollytorna?!

Själva ringen är kontrollvolymen. Dess begränsningsyta (rand) är kontrollytan.

Aha, okej, då fattar jag! Det som gjorde mig så förvirrad var att ringen var tecknad på samma sätt som röret som hela fluiden är omsluten av så jag trodde att det på samma sätt var ett sätt att visa vad som omslöt kontrollvolymen, inte att ringen själv var kontrollvolymen...

Men det är ändå lite mystiskt vad som händer med subscripten. De har ju explicit skrivit att hastighetsfältet inte varierar i $x$-led så borde inte integralen bara bli noll då eftersom vätskan dessutom är inkompressibel?

 Jo, det har du rätt i. Kommer de fram till något annat?

Nej, jag gick händelserna lite i förväg. Tack för hjälpen!

Hej igen. Jag kom att tänka på en till fråga om detta. Har man dessutom antagit att $r$ är så litet att trycket inte beror av $r$ utan endast av $x$?