För vilka värden på konstanten a har ekvationen ax^2-5x+2=0 exakt en rot?
Så, vi vet att om en andragradsekvation har en rot då ska (p/2)^2-q=0, till exempel (x-2)^2 då x=2.
Nu vet jag inte hur man gör riktigt, jag kommer ihåg att min lärare sa att man delar ekvationen med a?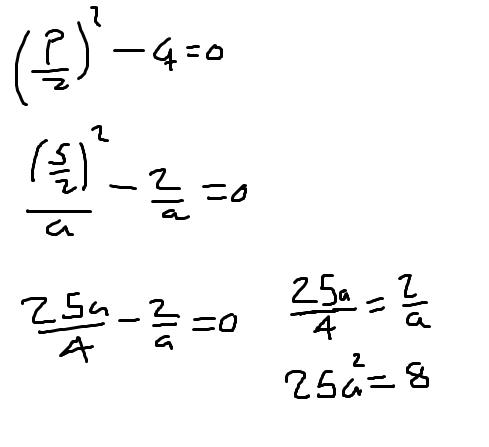 Jag har kommit så här långt.
Jag har kommit så här långt.
Där du har skrivit 25a/4 skall det vara något annat.
25/4a^2?
Här är en början. Jag skriver ut många steg, för annars gör jag slarvfel...
Exakt, skulle skriva det nyss. Alltså jag är så jävla stressad. Så då, sakta, får vi:
Jajamen. Snyggt.
Det är jättesvårt att räkna så långsamt att man gör rätt direkt, men man tjänar tid på det. :-)
Precis, tack för hjälpen! =)
Kolla med Diskrminants regler.
D=0 ger en lösning
D>0 ger två reala lösningar
D<0 ger två Imaginära lösningarnar
D= b2-4*a*2=0
D= (-5)2-4*a*2=0
25-4*a*2=0
Svaret är a=25/8