Förenkla matematisk uttryck
Hej!
Jag vet inte hur jag ska börja att förenkla detta uttryck:
Hade talen stått tvärtom så hade det inte varit något problem (och då använd Euklides' algoritm) men nu är ju nämnaren med x^4 jmf med täljaren som har x^3. Har provat med att sätta in 1,-1, 2, -2, 3, -3, 4, -4 för att se om det finns någon reell heltalsrot till de bägge uttrycken men det finns det inte. Har "fuskat" genom att knappa in de två uttrycken i en grafräknare och kunde konstatera att de två uttrycken har två gemensamma rötter dvs ca -2,27 respektive ca 1,30. Kunde även se på grafräknaren att tredjegradsuttrycket har tre reella rötter och fjärdegradsuttrycket har två reella rötter och två imaginära rötter.
4x^2 i täljaren kan man dela upp som (2x)^2 och även 8x till 2^3*x samt i nämnaren kan man dela upp 9 i 3^2.
Förslag mottages tacksamt!
WolframAlpha visar att de båda polynomen kan faktoriseras som respektive . Är du säker på att du har skrivit av uppgiften rätt? Andra faktorn i de båda polynomen är ju så lika.
Jag har nu tittat flera ggr och jag har skrivit av rätt. Enligt facit är svaret
Dock hänger jag inte med hur du lyckas faktorisera täljaren och nämnaren. Är det mångårig erfarenhet av räkning eller vad?
Smaragdalena har kanske skrivit av fel. Det går att fakturera ut (x^2+x-3) ur både nämnare och täljare.
Edit: och då får man fram det svar som står i facit
Om jag multiplicerar så får jag det till vilket inte är samma som ursprungspolynomen i nämnaren.
Dock så blir det rätt om man byter tecken i faktoriseringen av polynomet i nämnaren dvs =
Men jag förstår fortfarande inte hur jag ska tänka map hur jag ska kunna bryta ut (3x+1) respektive (x^2+3) och få en gemensam polynom på i både nämnare och täljare
Fotografen skrev:Om jag multiplicerar så får jag det till vilket inte är samma som ursprungspolynomen i nämnaren.
Ja, det skall vara x^2+x-3
Men hur man ser det ...
Jag vill gärna lära mig hur jag ska tänka då jag ämnar bli matematiklärare på högstadiet och skolverket "kräver" att man kan denna typ av matematik för att få undervisa på högstadiet. Ju mer man räknar ju mer samband och mönster ser man. Jag vill se den "röda tråden" så att jag förstår hur man ska tänka.
Hemsidan https://www.wolframalpha.com/examples/mathematics/ är ju väldigt effektiv men jag vill gärna lära mig. Man ska kanske bara sitta och prova sig fram till ett sätt att faktorisera ett polynom?
Om du tror att det skall gå att förkorta något så måste samma faktor gå att bryta ut ur både täljare och nämnare:
Det polynom med högst grad som det är någon mening med att bryta ut är på formen
Varför inte x^3? Ja, det ser du säkert.
De bägge utbrytningarna blir:
3x^3 +4x^2 −8x−3=(ax^2+bx+c)(dx+e) samt
x^4 +x^3 +3x−9=(ax^2+bx+c)(x^2+f) ingen variabel framför x^2 här, right?
Nu kan du direkt se att a=3 (ekv 2) och d=1
Vi skriver om igen och sätter in värdena:
3x^3 +4x^2 −8x−3=(3x^2+bx+c)(x+e)
x^4 +x^3 +3x−9=(3x^2+bx+c)(x^2+f)
Får du fram resten av variablerna? Genom att jämföra tex alla x^2 termer
Tex i ekv 1: 3+b=4 och så vidare
Detta går ju om man vet/tror att det skall gå att bryta ut och förkorta något.
Eftersom det står x^4 och -9 i nämnaren (bland annat) kan man prova med roten ur 3 och se vad som händer. Men det kom jag på först efter att ha läst det andra har skrivit här.
En sån här uppgift torde inte komma ens på gymnasiet, annat än som kul extrafråga åt den mest ambitiöse, och rakt inte i grundskolan. Tycker jag, men jag är inte lärare.
Ja, jag hade skrivit av fel - -3x istället för 3x. Om man vill göra faktoriseringen utan WolframAlpha (som känns lite fuskigt i sammanhanget) kommer jag inte på någon bättre metod än den som joculator nämner.
En teoretiskt möjligt alternativ är ju att lära sig en generell metod för att lösa tredjegradsekvationer, använda den för att faktorierna täljaren och sedan använda polynomdivision för att testa olika kombinationer av faktorer för att se om det går att faktorierna nämnaren med dem.
Men de flesta lär sig ju aldrig en generell metod för att lösa tredjegradare...
joculator skrev:Om du tror att det skall gå att förkorta något så måste samma faktor gå att bryta ut ur både täljare och nämnare:
Det polynom med högst grad som det är någon mening med att bryta ut är på formen
Varför inte x^3? Ja, det ser du säkert. Det borde vara för att man inte kan bryta ut något högre än x^2 i täljaren då det högsta är x^3De bägge utbrytningarna blir:
3x^3 +4x^2 −8x−3=(ax^2+bx+c)(dx+e) samt
x^4 +x^3 +3x−9=(ax^2+bx+c)(x^2+f) ingen variabel framför x^2 här, right?
Antar att det beror att vi redan har en koefficient a framför x^2 i det antagna gemensamma polynomet.
Nu kan du direkt se att a=3 (ekv 2) och d=1
Satt och kollade på detta och funderade på varför man skulle sätta a=3 och d=1 och inte tvärtom. Sedan när jag satt och tänkte så måste väl a=1 och d=3 dvs tvärtom eftersom det gemensamma polynomet är (x^2+x-3) dvs a=1.
Vi skriver om igen och sätter in värdena:
3x^3 +4x^2 −8x−3=(3x^2+bx+c)(x+e)
x^4 +x^3 +3x−9=(3x^2+bx+c)(x^2+f)
Får du fram resten av variablerna? Genom att jämföra tex alla x^2 termer
Tex i ekv 1: 3+b=4 och så vidare
Här är jag inte riktigt med, vad definierar du som ekv 1 (även ekv 2 ovan) ? Sedan förstår jag inte hur du tänker när du skriver 3+b = 4 då koefficienten b är enbart för x och inte x^2
Jag är sådan så att jag frågar (efter det att jag har försökt tänka själv) tills jag har fått det förklarat så att jag har förstått hur man ska lösa en uppgift.
Detta går ju om man vet/tror att det skall gå att bryta ut och förkorta något.
Mitt lilla förslag med x^4 och 3 var inte så användbart om man inte vill hålla på med imaginära tal också, för en lösning är ju 3i (som det visar sig).
Men, Euklides fungerar ju bra. Se bild. Och då kanske jag ändå anser att en lärare ska kunna det här, men däremot lär uppgiften inte komma för en elev.
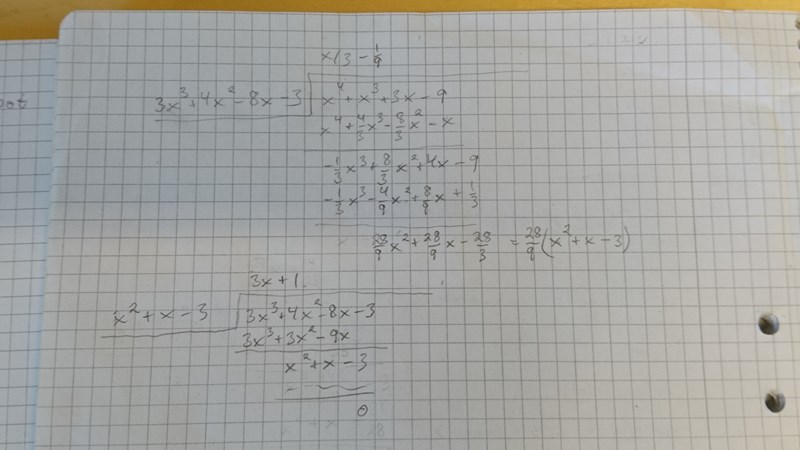
Nu har jag tänkt.....
Om det ska finnas något gemensamt polynom till de bägge talen så kan man ju lika gärna invertera divisionen och få x^4.../x^3 och gör man det så får jag samma polynom som man ska förkorta med dvs och använder man det och utför polynomdivision på båda talen i täljare respektive nämnare så får man fram (3x+1) respektive .
Tänker på a delare b = > a delare b*c
Fotografen skrev:joculator skrev:Om du tror att det skall gå att förkorta något så måste samma faktor gå att bryta ut ur både täljare och nämnare:
Det polynom med högst grad som det är någon mening med att bryta ut är på formen
Varför inte x^3? Ja, det ser du säkert. Det borde vara för att man inte kan bryta ut något högre än x^2 i täljaren då det högsta är x^3De bägge utbrytningarna blir:
3x^3 +4x^2 −8x−3=(ax^2+bx+c)(dx+e) samt
x^4 +x^3 +3x−9=(ax^2+bx+c)(x^2+f) ingen variabel framför x^2 här, right?
Antar att det beror att vi redan har en koefficient a framför x^2 i det antagna gemensamma polynomet.
Nu kan du direkt se att a=3 (ekv 2) och d=1
Satt och kollade på detta och funderade på varför man skulle sätta a=3 och d=1 och inte tvärtom. Sedan när jag satt och tänkte så måste väl a=1 och d=3 dvs tvärtom eftersom det gemensamma polynomet är (x^2+x-3) dvs a=1.
Vi skriver om igen och sätter in värdena:
3x^3 +4x^2 −8x−3=(3x^2+bx+c)(x+e)
x^4 +x^3 +3x−9=(3x^2+bx+c)(x^2+f)
Får du fram resten av variablerna? Genom att jämföra tex alla x^2 termer
Tex i ekv 1: 3+b=4 och så vidare
Här är jag inte riktigt med, vad definierar du som ekv 1 (även ekv 2 ovan) ? Sedan förstår jag inte hur du tänker när du skriver 3+b = 4 då koefficienten b är enbart för x och inte x^2
Jag är sådan så att jag frågar (efter det att jag har försökt tänka själv) tills jag har fått det förklarat så att jag har förstått hur man ska lösa en uppgift.
Detta går ju om man vet/tror att det skall gå att bryta ut och förkorta något.
Javisst, det är a=1 och d=3 som gäller. Slarvigt av mig. Jag skyller på copy-waste. Bra att du såg det.
Jag tror du får se hela mitt lösningsförslag som en skiss. Massor av slarvfel. Jag ber om ursäkt.
Det blir rätt jobbigt att få fram de andra variablerna och jag tror inte att detta är rätt väg att gå.
Ja, det går men det är inte roligt.
Det verkar som om ni missade mitt inlägg.
@joculator och @smaragdalena mfl. Jag är mkt tacksam att ni hjälper folk med matematiska problem och kommer med input. Själv vet jag att det är oerhört lätt att göra slarvfel när man sitter och räknar algebra. Har t.ex. börjat att skriva minus med röd penna för att inte missa något. Tycker det blir en extra hjälp om man använder olika färger i beräkningar, på samma sätt som det i vissa matematiska program idag finns olika färger för olika kommandon.
Hur som helst så ska ni ha stort tack för hjälpen!
Laguna skrev:Det verkar som om ni missade mitt inlägg.
Är du medveten om att du har vänt på kvoten? Du har beräknat
medans man i uppgiften frågar efter
Detta är en ganska framkomlig väg för att lösa uppgiften, men jag tycker att du bör förklara hur du gör lite utförligare. :-)
Laguna skrev:Det verkar som om ni missade mitt inlägg.
Jag kom på samma tillvägagångssätt som du men en timme senare.
a delare b => a delare b*c jmf med b delare a => b delare a*c så måste ju c vara samma för bägge polynomen. Jag fick inte ihop det hur man skulle utföra division med x^3 i täljaren och x^4 i nämnaren men genom att vända på divisionen så går det bra och bägge uttrycken måste ju ha c dvs i sig om det ska kunna gå att förkorta. Sedan får man använda ursprungspolynomen och dividera med så får man fram .
AlvinB skrev:Laguna skrev:Det verkar som om ni missade mitt inlägg.
Är du medveten om att du har vänt på kvoten? Du har beräknat
medans man i uppgiften frågar efter
Detta är en ganska framkomlig väg för att lösa uppgiften, men jag tycker att du bör förklara hur du gör lite utförligare. :-)
Jag har använt Euklides algoritm för att hitta en gemensam faktor, vilket frågestälkaren redan var inne på. Att det är en kvot från början har ingen betydelse. När du har resultatet från Euklides kan du förenkla den kvoten.
Laguna skrev:AlvinB skrev:Laguna skrev:Det verkar som om ni missade mitt inlägg.
Är du medveten om att du har vänt på kvoten? Du har beräknat
medans man i uppgiften frågar efter
Detta är en ganska framkomlig väg för att lösa uppgiften, men jag tycker att du bör förklara hur du gör lite utförligare. :-)
Jag har använt Euklides algoritm för att hitta en gemensam faktor, vilket frågestälkaren redan var inne på. Att det är en kvot från början har ingen betydelse. När du har resultatet från Euklides kan du förenkla den kvoten.
Ditt sätt att spalta upp Euklides algoritm såg på pricken ut som polynomdivision. Det var ett missförstånd från min sida.
I alla fall, så här hade man kunna lösa det genom enbart polynomdivision:
Om det ska gå att förenkla bråket måste det finnas ett sätt att bryta ut ur och få svaret som den andra faktorn. Utför man polynomdivisionen delat med får man:
Vi kan sedan applicera samma princip genom att förenkla bråket vi får i högerparentesen. Denna gången går divisionen jämt upp, vilket ger oss:
Tar man en gemensam nämnare i högerparentesen kan den förenklas avsevärt:
Med denna faktorisering kan ursprungsbråket ganska enkelt förenklas till:
Varje polynom q(x) med reella koefficienter är en produkt av polynom som i sig själva har reella koefficienter som antingen är 1) av första graden eller 2) av andra graden och saknar reella nollställen.
Med denna kunskap i bakhuvudet försöker vi hitta en eller flera gemensamma faktorer. Vi börjar med tredjegradspolynomet eftersom det verkar enklast.
Det första vi undersöker är om något polynomets rötter är rationell. För en rationell rot måste och enligt rationella rotsatsen. De tal som kan komma i fråga är . Vi finner att är en rot. En rättfram polynomdivision ger oss
Eftersom uppenbarligen inte är en rot till fjärdegradspolynomet är den enda möjliga gemensamma faktorn (eller någon av dess delfaktorer, varje polynom ska kunna skrivas som en produkt av första och andragradspolynom, se ovan). Vi kontrollerar med polynomdivision






