Förklaring av Clairauts Sats (Bevis)

Om en funktion f är kontinuerlig på intervallet [a, b] och deriverbar på intervallet (a, b) så gäller det att f(b) - f(a) = f’(c)(b - a) för något värde c sådant att a < c < b.

Kontinuitet är viktigt för många satser som du ofta använder. Exempelvis gäller medelvärdessatsen, som du nämnde för kontinuerliga funktioner. I detta bevis använder dem att $\lim_{x\to a}h\left(x\right) = h\left(a\right)$, vilket stämmer om $h$ är kontinuerlig i $a$ och inte nödvändigtvis om $h$ ej är kontinuerlig. 

EDIT: Rätta allt jag säger eller om något låter konstigt eller fel är kontroversiellt

Ahh jag hittade en dunder bild (imo):

Så här är sekantens (linjen som skär punkterna) lutning:

$\frac{f\left(b\right)-f\left(a\right)}{b-a}$, detta är sekantens lutning (d.v.s derivata) 

Så kolla det medelvärdesatsen säger är att om en funktion är:

-kontinuerlig, så kan vi inte hoppa över punkten c.

samt

-deriverbar (inga vassa hörn, för vid ett hörn så är det inte deriverbart kanske)

så medför det 

Att någonstans på grafen f(x) finns det en punkt (c som är större än a men mindre än b) där lutningen vid den punkten sammanfaller med sekantens lutning, d.v.s

f'(c)=$\frac{f\left(b\right)-f\left(a\right)}{b-a}$ ty ovanstående kriterier.

Vilket är precis det du sade fast mer "dumifierat" lol! Tycker fortfarande att det är konstigt att funktion måste vara deriverbar på det öppna intervallet och inte det stängda. Hursomhelst! Hur gäller det i detta fallet? Jo när vi tillämpar medelvärdessatsen på F och G så innebär det att vid en punkt för F, som de kallade $\xi$så kommer det att vara lika med 

$F\text{'}\left(\xi \right)=\frac{F(a+h)-F\left(a\right)}{(a+h)-\left(a\right)}=\frac{F(a+h)-F\left(a\right)}{h}\iff hF\text{'}\left(\xi \right)=F(a+h)-F\left(a\right)$

och analogt gäller för G fast för en annan punkt för att det är en annan funktion. 

Sen vad som händer är att $\xi$=x och sen så deriveras högerledet i ekvationen för F(x)=f(x,b+h)-f(x,b) längre upp. Jag antar (min tolkning) att derivering m.a.p x är ty (b+h) och b är en fast punkt (eller mer lämpligt) så vi kan bara derivera m.a.p på en variabel, och det är x. Analogt gäller för G. 

Sen så används medelvärdessatsen slutligen igen och då borde det finnas en annan punkt där tangentens lutning=sekantens lutning. Frågan är nu bara var detta kom ifrån, hur gjorde de detta liksom?

Aja om vi nu använder medelvärdessatsen så får vi (DETTA ÄR VAD JAG TROR)

$f\text{'}{\text{'}}_{xy}(\xi ,\zeta )=\frac{f(\xi ,b+h)-f(\xi ,b)}{(b+h)-\left(b\right)}=\frac{f(\xi ,b+h)-f(\xi ,b)}{h}\iff hf\text{'}{\text{'}}_{xy}(\xi ,\zeta )=f(\xi ,b+h)-f(\xi ,b)$

analogt gäller för HL. 

Sen så stryks h och vi låter h $\to$ 0 vilket medför att vi får detta 

b < $\zeta$<b+0 = b < ζ<b och på grund av instägningssatsen eller vad den nu hette så är  ζ=b och vice versa gäller för theta, xi och eta ($\eta$). Visste inte att den hette eta btw. 

DÅ har Clairauts sats bevisats.

Edit: nu återstår det vad mer medelvärdessatsen kan användas till lol?

AlexMu skrev:

 I detta bevis använder dem att $\lim_{x\to a}h\left(x\right) = h\left(a\right)$, vilket stämmer om $h$ är kontinuerlig i $a$ och inte nödvändigtvis om $h$ ej är kontinuerlig. 

Menar du typ generellt sett då, så länge den bara är kontinuerlig i a så gäller det gränsvärdet?

Ja, man kan definiera kontinuitet som egenskapen att $\lim_{x\to a}f\left(x\right) = f\left(a\right)$. Detta gränsvärde gäller inte för, exempelvis funktionen $f\left(x\right)=\left\{\begin{array}{lc}1&x=0\\0&\text{annars}\end{array}\right.$ när $a=0$.

Men kontinuitet är en egenskap som är ett krav i massivs med satser som du sett i envariabelanalysen (och säker i flervariabel också!). Exempelvis medelvärdessatsen eller extremvärdessatsen (en kontinuerlig funktion på en kompakt mängd antar ett största och minsta värde). Alla kontinuerliga funktioner är integrerbara, etc. 

AlexMu skrev:

 $f\left(x\right)=\left\{\begin{array}{l}1,\;x=0\\0,\;\text{annars}\;\end{array}\right$ 

?

Sykey skrev:

?

Skrev fel i mitt uttryck.

hmm, jag har inte hört varken att alla kontinuerliga funktioner är integrerbara eller extremvärdessatsen. De är nya för mig!

Edit: så den antar BÅDE minsta och största värde? Märkte också att du sa kompakt mängd.

Är kompakt mängd att den är sluten och begränsad eller är det något annat.

Jag jämför lite med min envariabelkurs. Båda satserna var med i min, men extremvärdessatsen hade inte ett namn (dock användes den). En kompakt mängd är en sluten och begränsad mängd, ja.

I envariabeln använde vi bland annat extremvärdessatsen för att bevisa medelvärdessatsen. 

Detta skrev en annan kille om kompakt mängd, så han sa att det var något helt annat (på en annan tråd):

"Begreppet Kompakt är inte ett annat ord för sluten och begränsad och inte heller för att tilldela mått på areor i R². Det kan man göra utan begreppet kompakt. Det står inte där på tavlan för att åstadkomma detta. Om jag får gissa vad som står längre fram så kan det vara att f är likformigt kontinuerlig. begränsad och antar sitt max- och minvärde på D. Det följer nämligen av kompaktheten. Det Naytte skriver är inte en definition utan en viktig sats som gäller i Rⁿ. Det finns andra rum där den inte gäller."

Sykey skrev:

Tycker fortfarande att det är konstigt att funktion måste vara deriverbar på det öppna intervallet och inte det stängda.

Också, angående detta finns funktioner som är deriverbara i det öppna intervallet men ej det slutna. Ett exempel är $\sqrt[3]{x}$ på intervallet $[0,1]$. Denna funktion är kontinuerlig på intervallet och deriverbar på $(0,1)$, men den är ej deriverbar i $x=0$. 

Sykey skrev:

Detta skrev en annan kille om kompakt mängd, så han sa att det var något helt annat (på en annan tråd):

"Begreppet Kompakt är inte ett annat ord för sluten och begränsad och inte heller för att tilldela mått på areor i R². Det kan man göra utan begreppet kompakt. Det står inte där på tavlan för att åstadkomma detta. Om jag får gissa vad som står längre fram så kan det vara att f är likformigt kontinuerlig. begränsad och antar sitt max- och minvärde på D. Det följer nämligen av kompaktheten. Det Naytte skriver är inte en definition utan en viktig sats som gäller i Rⁿ. Det finns andra rum där den inte gäller."

Jag pratar just nu bara på $\mathbb R$ (eftersom det var i referens till envariabelanalysen) och där är sluten och begränsad ekvivalent med den mer "vanliga" definitionen av en kompakt mängd. Det stämmer inte nödvändigtvis för andra rum. 

Tillägg: 10 feb 2026 22:55

Kan dock nämna att sluten och begränsad är ekvivalent med kompakthet på $\mathbb R^n$ (Heine-Borel theorem). Jag vet inte exakt när det inte gäller, men jag tror det blir problem för rum med oändligt många dimensioner. 

AlexMu skrev:

Jag pratar just nu bara på $\mathbb R$ och där är sluten och begränsad ekvivalent med den mer "vanliga" definitionen av en kompakt mängd. Det stämmer inte nödvändigtvis för andra rum. 

Okej då kör vi på vad som gäller för R. Vad som gäller för andra rum har jag ingen aning vad som händer.

Okej men igen med ditt fall för x^(1/3). Bara för att det finns ett fall (det finns nog flera) så kör vi med öppna mängden. Tänk om jag hittar funktioner som är deriverbara på det stängda intervallet... så idk... fattar fortfarande inte... det känns onödigt (eller kanske mer från fall till fall?)

Om funktionerna är deriverbara på det slutna intervallet är de även deriverbara på det öppna intervallet och då gäller satsen!

Det enda jag menar är att om kravet för medelvärdessatsen var att funktionen är deriverbar på det slutna intervallet, så skulle mängden funktioner vi kan applicera satsen på att minska (då skulle vi inte kunna använda den på $\sqrt[3]{x}$). Ju svagare krav desto bättre!

AlexMu skrev:

Om funktionerna är deriverbara på det slutna intervallet är de även deriverbara på det öppna intervallet och då gäller satsen!

Det enda jag menar är att om kravet för medelvärdessatsen var att funktionen är deriverbar på det slutna intervallet, så skulle mängden funktioner vi kan applicera satsen på att minska (då skulle vi inte kunna använda den på $\sqrt[3]{x}$). Ju svagare krav desto bättre!

ahh, det är sant. Ett svagare krav är bättre för då kan vi använda den till mer tillfällen. Båda dina stycken är sanna. amen coolt! Faktiskt. Btw när du sa att f(x)=1 vid x=0 och f(x)=0 annars så menar du väl att funktionen inte är kontinuerlig eftersom den direkt hoppar från 1 till 0 (om vi zoomar in liksom) och därmed är den inte kontinuerlig så är den inte deriverbar? 

Edit: Är detta sant. Ej kontinuerlig --> ej deriverbar? 

En till sak: tror du detta är rätt resonerat (eller att epsilon är på rätt plats och att det inte ska stå a eller a+h eller så?)

Svagare krav är bra! 

Lite orelaterad kuriosa på temat med svaga krav: En av mina favoritsatser för analys i en variabel är att en funktion är (riemann) integrerbar om och endast om mängden av dess diskontinuiteter har mått noll (measure zero), vilket essentiellt betyder att mängden av alla diskontinuiteter inte tar upp någon "längd" på den reella linjen. Det som är faschinerande här är att det är en ekvivalens. Varje funktion med denna egenskap är integrerbar och varje integrerbar funktion har denna egenskap.

Detta är mycket svagare än satsen från tidigare att en kontinuerlig funktion är integrerbar. Mängden av en kontinuerlig funktions diskontinuiteter är ju den tomma mängden (som har mått noll). Med denna sats kan vi ha massvis med diskontinuiteter (oändligt många) och fortfarande veta att funktionen är integrerbar. 

> Är detta sant. Ej kontinuerlig --> ej deriverbar? 

Ja, det är negering av påståendet "Deriverbar $\implies$ kontinuerlig", vilket är sant. 

Och ja jag tycker det ser rätt ut. Det vi essentiellt gör i beviset är att applicera medelvärdessatsen i båda argument av funktionen. Vi håller ena argumentet konstant för att göra om funktionen till en funktion i en variabel så att satsen kan användas. Sedan låter vi det andra argumentet vara konstant för att upprepa processen och därmed ta två derivator (vilket är vårt mål!). 

Måtteori är fett!

Med mått noll avser man Lebesguemåttet, alltså ett särskilt mått. Det finns andra också.

AlexMu skrev:

Svagare krav är bra! 

Lite orelaterad kuriosa på temat med svaga krav: En av mina favoritsatser för analys i en variabel är att en funktion är (riemann) integrerbar om och endast om mängden av dess diskontinuiteter har mått noll (measure zero), vilket essentiellt betyder att mängden av alla diskontinuiteter inte tar upp någon "längd" på den reella linjen. Det som är faschinerande här är att det är en ekvivalens. Varje funktion med denna egenskap är integrerbar och varje integrerbar funktion har denna egenskap.

Detta är mycket svagare än satsen från tidigare att en kontinuerlig funktion är integrerbar. Mängden av en kontinuerlig funktions diskontinuiteter är ju den tomma mängden (som har mått noll). 

> Är detta sant. Ej kontinuerlig --> ej deriverbar? 

Ja, det är negering av påståendet "Deriverbar $\implies$ kontinuerlig", vilket är sant. 

Och ja jag tycker det ser rätt ut. Det vi essentiellt gör i beviset är att applicera medelvärdessatsen i båda argument av funktionen. Vi håller ena argumentet konstant för att göra om funktionen till en funktion i en variabel så att satsen kan användas. Sedan låter vi det andra argumentet vara konstant för att upprepa processen och därmed ta två derivator (vilket är vårt mål!). 

Ahh så det gäller att hålla de konstant för att kunna använda medelvärdessatsen, annars blir det lite svårt så att säga. Jag vet inte vad en diskontinuitet är, liksom det är väl när funktionen inte är kontinuerlig men det känns konstigt. Då måste funktionen ha en massa (mängd) kontinuiteter, det känns konstigt (det är la bara punkter nära varandra?). Eller... kanske inte så konstigt... Ahh vänta jag tror jag sett detta, eller något med riemannsummor. Att integraler är gränsvärdet av riemannsummor då x går mot noll? Vet inte varför de kallas riemann. 

Edit: är detta verkligen en sats dock jag trodde det var mer en per definition att integralen var dessa summor. Liksom här får du en kuriosa som du nog redan visste men integraltecknet är ett utsträckt "S" som står för summa.

Ja, en diskontinuitet är en punkt där funktionen inte är kontinuerlig. Funktionen $f\left(x\right)=\left\{\begin{array}{l}1,x=0\\0\;\text{ annars}\end{array}\right.$ har en diskontinuitet i $x=0$ och mängden diskontinuiteter blir då $\{0\}$, eftersom den är kontinuerlig överallt annars. Jag drog in ordet riemann för att det finns andra "typer" av integraler som är definierade på annorlunda sätt. Denna sats jag nämnde är dock specikt för riemannintegralen (den "vanliga" integralen), annat gäller nog för andra typer av integraler. 

AlexMu skrev:

Ja, en diskontinuitet är en punkt där funktionen inte är kontinuerlig. Funktionen $f\left(x\right)=\left\{\begin{array}{l}1,x=0\\0\;\text{ annars}\end{array}\right.$ har en diskontinuitet i $x=0$ och mängden diskontinuiteter blir då $\{0\}$, eftersom den är kontinuerlig överallt annars. 

ahh det make:ar sense och mängden kontinuiteter är $x\in \mathrm{ℝ}\backslash \left\{0\right\}$, eller?

Det finns andra typer av integraler? Ahh vänta, ahh jag kan några namn, dubbelintegraler (R²), trippelintegraler (R³) och multipelintegraler (Rⁿ).

Ja precis! Funktionen 

$g(x)=\left\{\begin{array}{l}1,x=1/n\\0\;\text{annars}\end{array}\right.$ där $n$ är ett positivt heltal är diskontinuerlig för $1, 1/2, 1/3, ...$ och kontinuerlig överallt annars. Här blir då mängden av diskontinuiteter $\{1, 1/2,1/3,\dots\}$

ahh, så hade man ritat ut den grafen så hade den haft massa punkter vid olika x-värden fast på samma y-värde som alltid är 1. Den hoppar alltså oändligt många gånger efter x=0? 

Sykey skrev:

Det finns andra typer av integraler? Ahh vänta, ahh jag kan några namn, dubbelintegraler (R²), trippelintegraler (R³) och multipelintegraler (Rⁿ).

Jag tror det fortfarande räknas som riemannintegraler, i alla fall på det sätt som de definieras i flervariabelanalys. Jag har inte jättegod koll på andra typer av integraler, men den mest kända integralen som inte är riemann är Lebesgueintegralen. 

AlexMu skrev:

Sykey skrev:

Det finns andra typer av integraler? Ahh vänta, ahh jag kan några namn, dubbelintegraler (R²), trippelintegraler (R³) och multipelintegraler (Rⁿ).

Jag tror det fortfarande räknas som riemannintegraler, i alla fall på det sätt som de definieras i flervariabelanalys. Jag har inte jättegod koll på andra typer av integraler, men den mest kända integralen som inte är riemann är Lebesgueintegralen. 

Åhh, gudars vad är det för flummigt namn? Lebesgueintegralen? Uschh lol

De räknas definitivt som Riemannintegraler och faktum är att de kan definieras helt analogt till Riemannintegralen! Alltså verkligen nästan identiskt.

Ahh så det finns bara Riemannintegraler. Plottwist: alla integraler är riemannintegraler 

Sykey skrev:

ahh, så hade man ritat ut den grafen så hade den haft massa punkter vid olika x-värden fast på samma y-värde som alltid är 1. Den hoppar alltså oändligt många gånger efter x=0? 

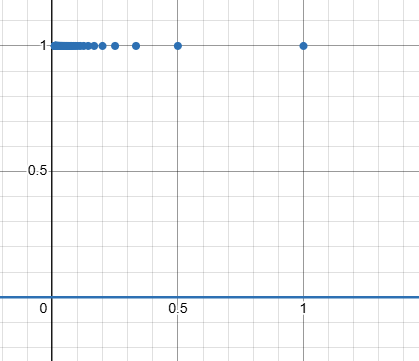Funktionen skulle ungefär se ut såhär (där jag inte lyckats rita ut "hålen" i linjen $y=0$ där funktionen hoppar till $1$)