Förstå induktionsbevis
Hej pluggakuten!
Jag är ivrig att lära mig induktionsbevis, och jag tror jag (kanske) förstår den övergripande principen, men jag fastnar i det här steget:
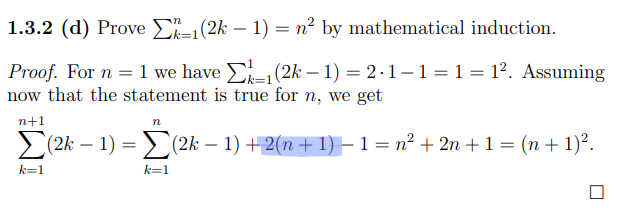
Är det att man skriver om i termer av ,
och för att dom två ska bli samma så tar man först och sen så lägger man till en sista iteration för n+1?
När vi vill bevisa en hypotes via induktionsbevis måste vi använda något vi redan vet, vårt induktionsantagande. Vårt induktionsantagande i den här uppgiften är att:
Med hjälp av detta induktionsantagande vill vi alltså visa att:
Vi inser att vi kan dela upp summan:
Vi har alltså visat att om hypotesen är sann för , så måste den vara sann för . Här kommer basfallet in. Eftersom vi vet att hypotesen är sann för , vet vi att den också måste vara sann för . Men om vi vet att den är sann för , måste den också vara sann för , och så vidare.
naytte skrev:När vi vill bevisa en hypotes via induktionsbevis måste vi använda något vi redan vet, vårt induktionsantagande. Vårt induktionsantagande i den här uppgiften är att:
Med hjälp av detta induktionsantagande vill vi alltså visa att:
Vi inser att vi kan dela upp summan:
Vi har alltså visat att om hypotesen är sann för , så måste den vara sann för . Här kommer basfallet in. Eftersom vi vet att hypotesen är sann för , vet vi att den också måste vara sann för . Men om vi vet att den är sann för , måste den också vara sann för , och så vidare.
Tack för detta naytte! Det blev tydligare med din framställning, jag är med på banan!
Kul att svaret var till hjälp!
Jag minns att induktion var en av de sakerna jag hade svårt att greppa när jag först stötte på det - inte för att det är särskilt svårt egentligen, utan för att alla förklaringar jag hittade var rent mög. Det verkar som att stora delar av didaktiken har fastnat i vissa paradigmer ("så ska man förklara detta") och dessa förklaringar är oftast askassa.
naytte skrev:Kul att svaret var till hjälp!
Jag minns att induktion var en av de sakerna jag hade svårt att greppa när jag först stötte på det - inte för att det är särskilt svårt egentligen, utan för att alla förklaringar jag hittade var rent mög. Det verkar som att stora delar av didaktiken har fastnat i vissa paradigmer ("så ska man förklara detta") och dessa förklaringar är oftast askassa.
Ja! Har märkt att det är bra att skriva om bevis så att de passar en själv, och det är skönt att man kan läsa flera olika beskrivningar och bevis för en och samma sats. Lite som att lysa upp ett objekt med en ficklampa från flera olika håll så att man får en bättre uppfattning :)


