Förstår inte lösningen (diffar)
Jag vet att några av er har redan förklarat flera gånger första ordningen diffar men nu har jag nått den här tröttpunkten där jag fattar inte egna anteckningar.

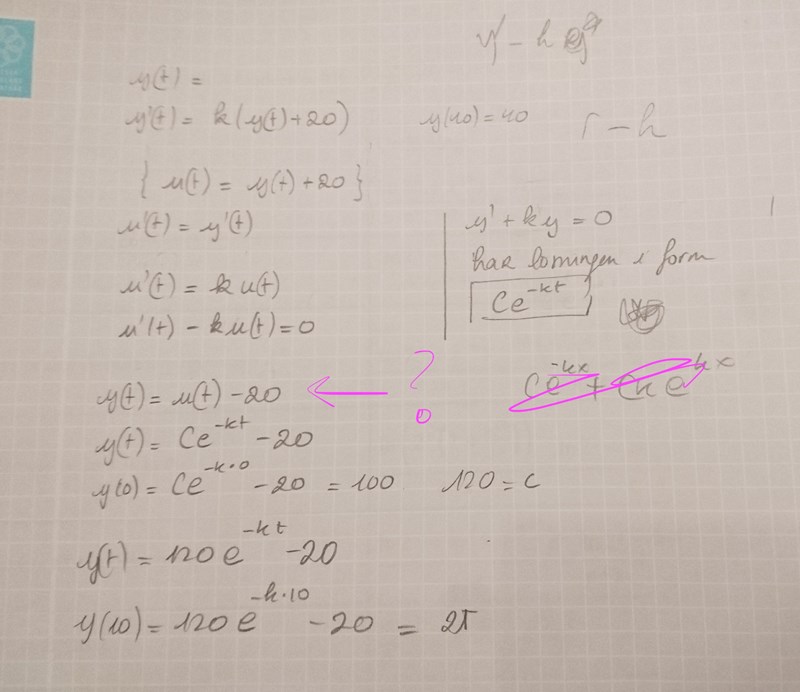
Varför kan man skriva u(t) - 20 = y(t)? Är det för att vi gjorde variabel bute eller för att det är -20 ute?

Kan någon förklara EXTRA tydligt så att även en hund kan klara tentan?
Vi substituerar .
Om vi subtraherar på båda sidor får vi:
Hänger du med på det?
Ja, tack. Min inre hund förstår. Varför får vi information att det är -20 ute?
Kanske för att ni skall förstå differentialekvationen?
joculator skrev:Kanske för att ni skall förstå differentialekvationen?
Isf är det failat.
På viljet sätt skulle diffekvationen se annorlunda ut om utomhustemperaturen var 0°C istället?
dajamanté skrev:joculator skrev:Kanske för att ni skall förstå differentialekvationen?
Isf är det failat.
Förlåt, jag trodde du undrade varför ni fått information som ni inte behöver för att lösa uppgiften. Jag gissade då på att det var för att öka er förståelse för varför diff.ekv. ser ut som den gör.
Om du ser på det y(t) som du kommer fram till. Vad händer om du har ett stort t? Vad får y(t) för värde då? Vad beror det på?
Varför blir vattnet -20 grader? Varför inte tex 17 grader?
joculator skrev:dajamanté skrev:joculator skrev:Kanske för att ni skall förstå differentialekvationen?
Isf är det failat.
Förlåt, jag trodde du undrade varför ni fått information som ni inte behöver för att lösa uppgiften. Jag gissade då på att det var för att öka er förståelse för varför diff.ekv. ser ut som den gör.
Du gissade nog rätt. Ja men det är precis det jag menade! Vi är åtminstone två som har glömt egen lösning, så...
Om du ser på det y(t) som du kommer fram till. Vad händer om du har ett stort t? Vad får y(t) för värde då? Vad beror det på?
Varför blir vattnet -20 grader? Varför inte tex 17 grader?
Alltså jocu, jag har INGEN aning :/. Jag vill bara spy när jag ser en differentialekvation.
- Om så är derivatan .
- Om uppfyller ODE:n så kommer att uppfylla ODE:n
- Lösningarna till ODE:n är funktionerna .
- Dessa funktioner motsvarar funktionerna
Om grader Celsius så blir grader Celsius och . För att bestämma konstanten behöver du veta temperaturen vid ytterligare en tidpunkt; du får veta att grader Celsius vilket gör att du kan skriva
.
Temperaturen är grader Celsius vid tidpunkten minuter efter att det kokande vattnet ställts ut i kylan.
.
Tack Albiki.
Jag bör nog ta en matte 4 bok efter tentan och repetera.





