Förvirring kring Kirchhoffs spänningslag
Halloj!
Jag sitter med några grundläggande uppgifter i elektrisk mätteknik och håller på att jobba med en uppgift om Kirchhoffs spänningslag.
Min förståelse hittills hade varit att Kirchhoffs spänningslag säger att det sammanlagda spänningsfallet i en krets är lika med kretsens polspänning. Alltså, om vi har spänningsfall samt polspänning så ska det gälla . På Wikipedia står det däremot att summan av spänningsfallen (potentialändringarna) ska vara noll. Jag förstår logiken bakom detta (potentialändringen över en komponent måste ju vara negativ) men jag har svårt att förenliga det med verkligheten.
Då vi mäter spänningar med en voltmeter får vi ett positivt värde över en komponent. Ohms lag ger ju också positiva värden på då vi använder konventionell strömriktning i t.ex. en likströmskrets som denna:
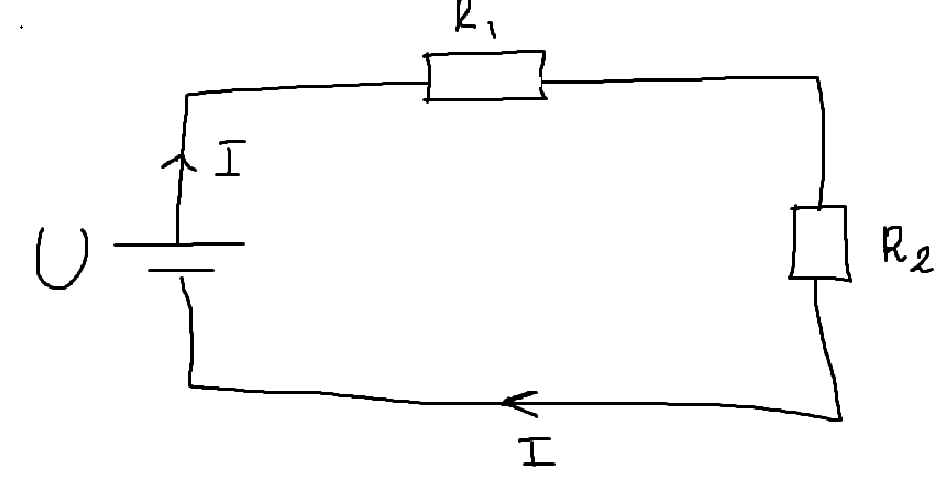
Ohms lag säger att samt . Det var därför jag ursprunligen tänkte att . Eftersom alla ingående storheter är positiva gäller det ju åtminstone inte att ...
Hej!
Jag tycker Wikipedia är konsistent med din förståelse ifall den använder ordet "potentialskillnader", eller "potentialändringar" vilket (till skillnad från ordet "potentialfall") även intuitivt känns att de lika gärna kan mätas som negativa. När du summerar potentialskillnaderna i din figur mätt med voltmeter så blir ju batterispänningen U negativ om du mäter med voltmetern på samma sätt över alla komponenter i kretsen.
Har du läst elmag än? Kirchoffs spänningslag är ju inget annat än ett uttryck för Maxwells tredje ekvation (Faradays lag) som säger att det elektriska fältet längs en sluten loop är lika stort som tidsderivatan av det magnetiska fluxet genom ytan som loopen innesluter. Har du DC - dvs inget tidsvarierande magnetfält, så blir högerledet noll.
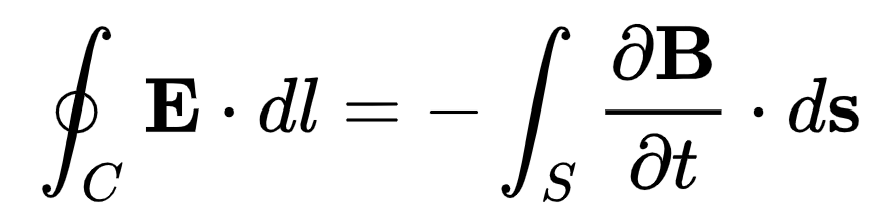
Det finns ingen motsägelse här. Om jag ska tolka "din förståelse" (som jag tycker är korrekt) så börjar vi i kretsens högsta potential (spänningskällans pluspol). För varje resistor i din bild faller spänningen tills vi hamnar på kretsens lägsta potential (spänningskällans minuspol). Dvs summan av spänningsfallen är lika med U.
Men nu har vi gått igenom alla komponenter utom spänningskällan. Wikipedia pratar om alla komponenter. Vi måste fullborda potentialvandringen så att vi har gått runt hela kretsen. Då behöver vi "klättra upp" från lägsta potentialen till högsta genom spänningskällan. Det är inget spänningsfall. Det är en spänningsökning dvs annat tecken. Och summan blir noll eftersom vi är tillbaka där vi började.
naytte skrev:Eftersom alla ingående storheter är positiva gäller det ju åtminstone inte att ...
Som Peter också nämner. Beroende på hur man definierar spänningarna är antingen alla termer förutom spänningskällan negativa, eller tvärtom. Därför blir det 0.
MrPotatohead skrev:naytte skrev:Eftersom alla ingående storheter är positiva gäller det ju åtminstone inte att ...
Som Peter också nämner. Beroende på hur man definierar spänningarna är antingen alla termer förutom spänningskällan negativa, eller tvärtom. Därför blir det 0.
Då vi mäter spänningar med en voltmeter får vi ett positivt värde över en komponent.
Det enda viktiga är att definiera spänningarna på samma sätt hela tiden, när de summeras. Och i din mätteknikkurs så gör du den definititionen, rent praktiskt, genom att vara konsekvent med på vilken sida av mätobjektet du sätter voltmeterns svarta- respektive röda prob. Ni gör säkert några laborationer. Passa på proba "åt andra hållet" på ett mätobjekt så kommer du se att voltmeterns mätvärde byter tecken.




