Fråga 1117, Matte 2b Origo
Visa spoiler
Skriv ditt dolda innehåll här
Såg på gamla pluggakuten att denna frågan var ställd men uppgiften blev aldrig löst eller förklarad så efter en halvtimme brottandes med denna uppgiften har jag äntligen svaret som kommer i bilden nedan, hoppas det blir hjälp!
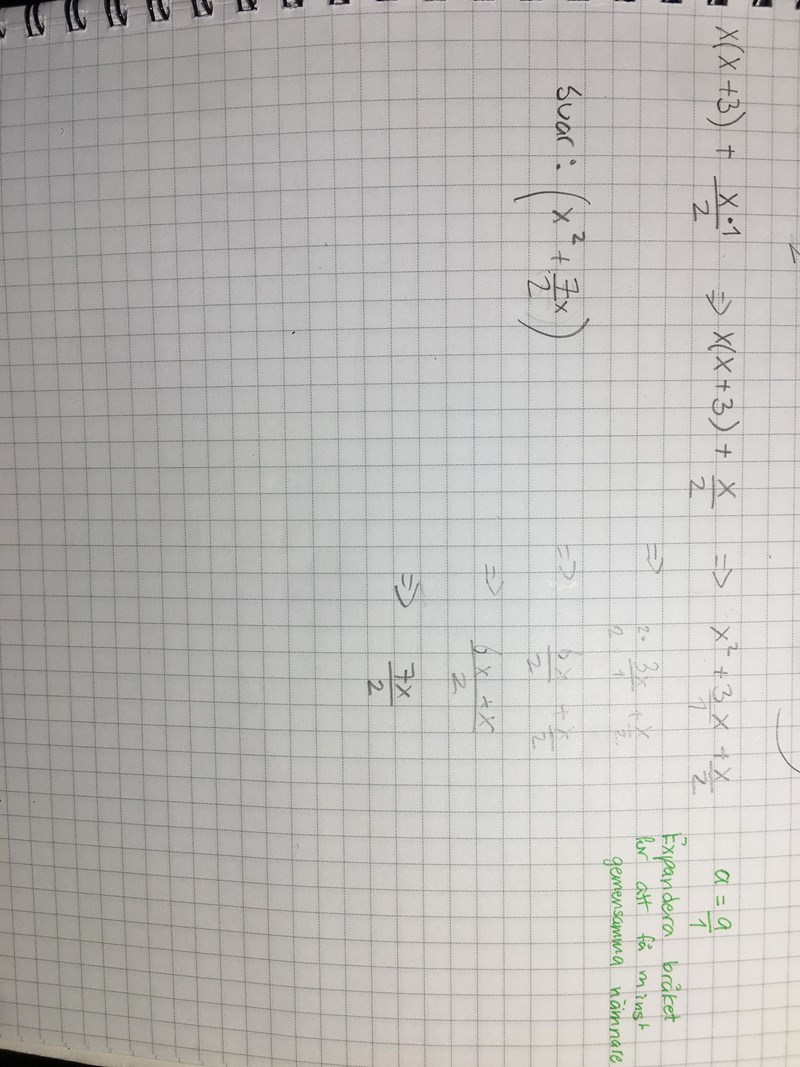
1117 ställ upp ett uttryck för figurens area och f örenkla det så långt som möjligt.
örenkla det så långt som möjligt.
Det ser ut som om du ställt upp fel?
är korrekt för undre delen, men den lilla triangeln blir
Edit: Slarv av mig det ska vara och då blir det som du skriver.
Spontant borde man kunna räkna det också som:
ConnyN skrev:Det ser ut som om du ställt upp fel?
är korrekt för undre delen, men den lilla triangeln blir
Edit: Slarv av mig det ska vara och då blir det som du skriver.
Tack för korrektionen! Men skulle du kunna förklara varför man har dubbel parantes?
Det var för att du skulle se alla steg.
1) Höjden på triangeln är det blir när vi tar bort parenteserna.
2) Sedan hade jag ju glömt att vi måste multiplicera med x, då behövde vi en parentes runt hela uttrycket.
och eftersom det är en triangel dividera med två.
Är du med då?
ConnyN skrev:Det var för att du skulle se alla steg.
1) Höjden på triangeln är det blir när vi tar bort parenteserna.2) Sedan hade jag ju glömt att vi måste multiplicera med x, då behövde vi en parentes runt hela uttrycket.
och eftersom det är en triangel dividera med två.
Är du med då?
Yes! Tack:)
tomast80:s lösning är värd lite uppmärksamhet också. Det tog en stund innan jag fattade hur han tänkt.
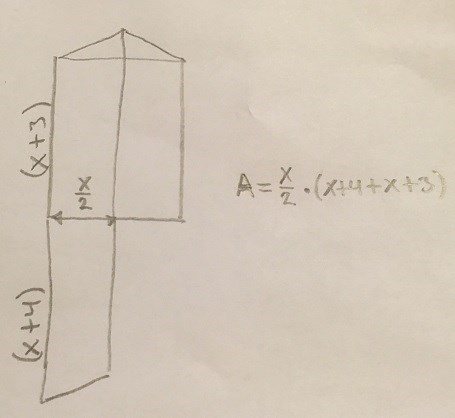
Som jag tror så delade han helt enkelt figuren mitt itu och vred ena halvan så vi fick en romboid och då blev det plötsligt den enkla beräkning han föreslog.
Snyggt Tomas!
Tack ConnyN!
Så avancerat hade jag inte tänkt faktiskt. Jag tänkte att basen är och genomsnittliga höjden är:
.
Det gav sedan arean:



