Funktionmängd
1) När jag ritar med GeoGebra får jag två olika grafe
2) domain till. f(x)
(X-2)/x=>0. Om x#0
x-2=>0. X#0
x=>2
vad är felet jag ser att negativa talen ligger också i domainen men jag kan inte hitta i lösningen
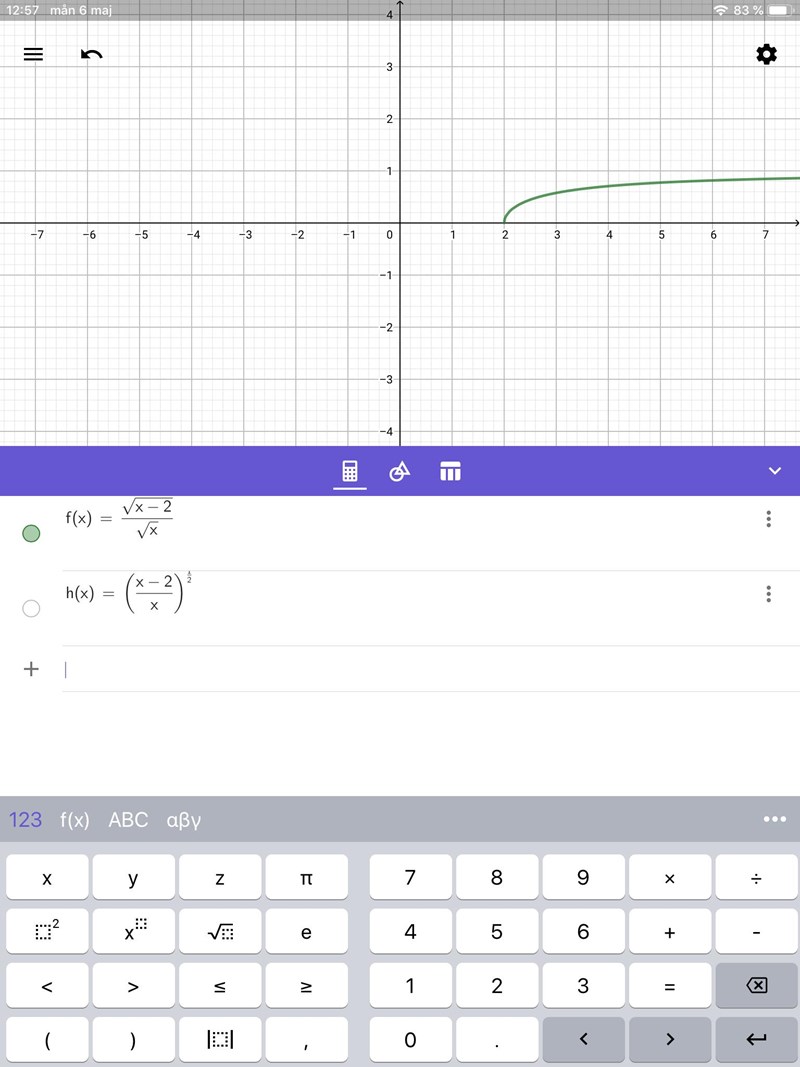
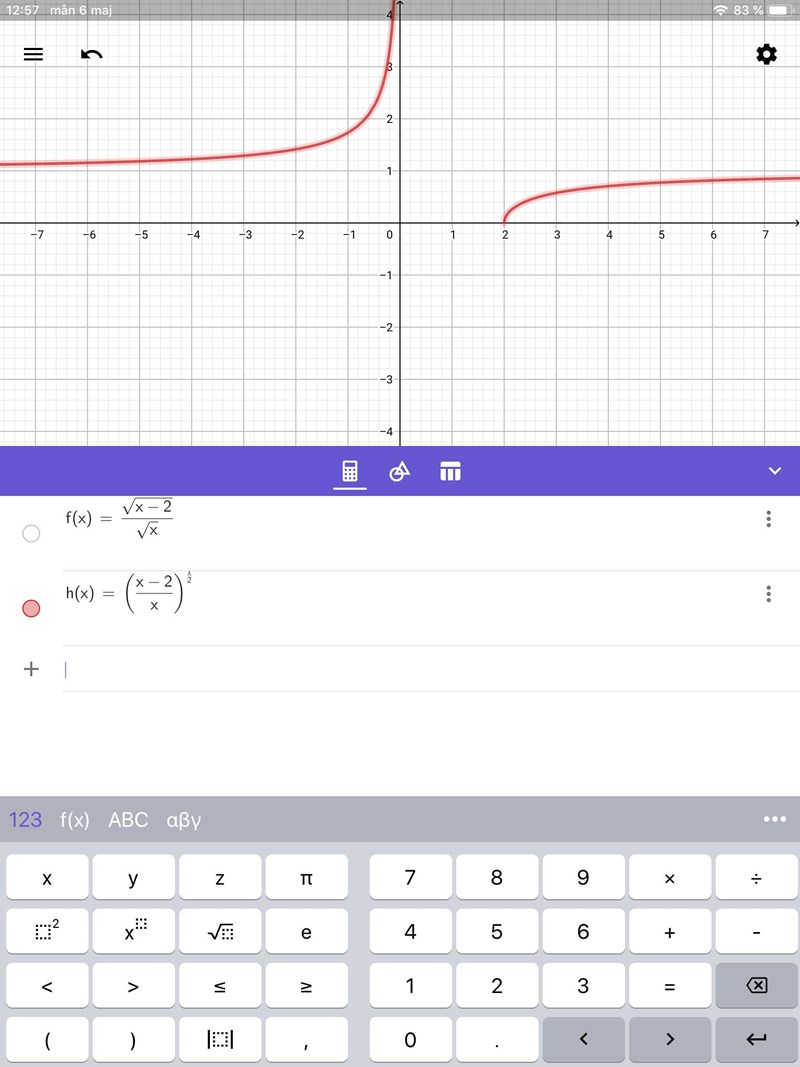
Vad är ?
Odefinerat
RAWANSHAD skrev:Odefinerat
Ja (eller typ...), och därför kan ju inte intervallet ingå i dess definitionsmängd.
Om x= -1.
Det är ok men vad är felet
RAWANSHAD skrev:Om x= -1.
Det är ok men vad är felet
Kalla och .
Då har vi att
och att
, vilket inte är ett reellt tal.
Problemet är att likheten endast gäller för positiva och .
Dvs det gäller inte att för alla .
f(-1) existerar om eftersom uttrycket under rottecknet är positivt, men g(-1) existerar inte om eftersom man inte kan dra roten ur ett negativt tal.
Ni tänker så. Jag förstod knappt frågan så jag antog att det var den första funktionen han försökte använda och sedan använde massa algebra för att få resten.
woozah skrev:Ni tänker så. Jag förstod knappt frågan så jag antog att det var den första funktionen han försökte använda och sedan använde massa algebra för att få resten.
Jag tror att frågan gäller varför Geogebra ritar olika grafer till och .
Ja det stämmer , det är min fråga
RAWANSHAD skrev:Ja det stämmer , det är min fråga
OK och känner du att du har fått svar?



