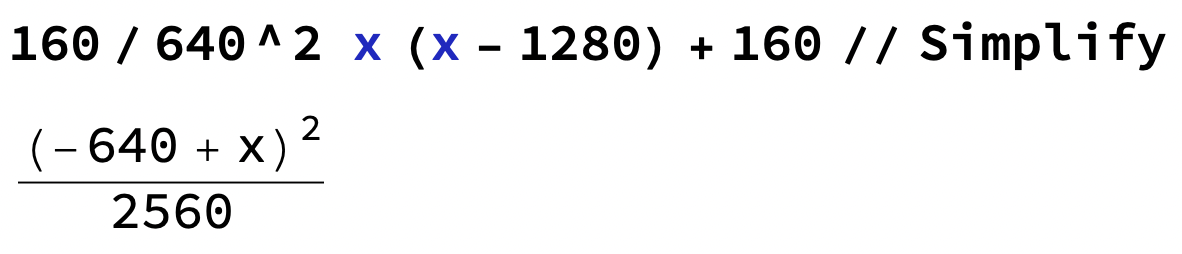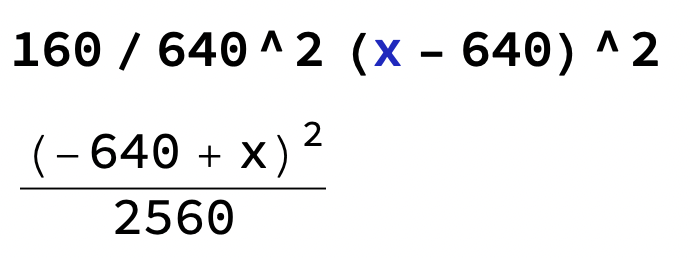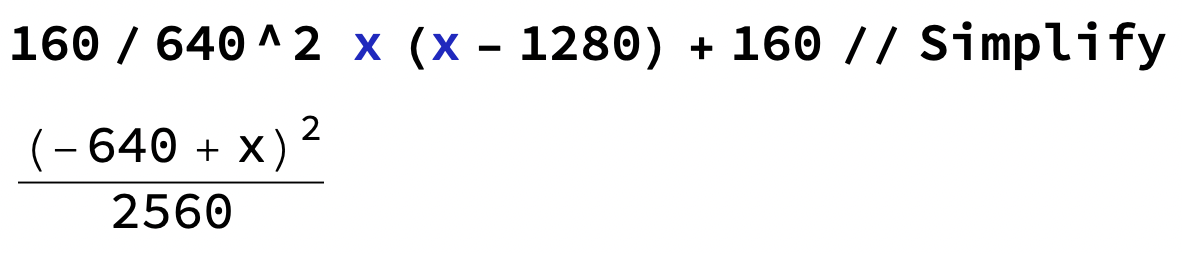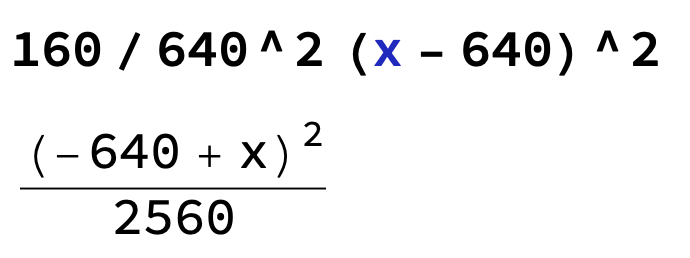Golden gate-bron i San Francisco, USA, är en av världens längsta hängbroar.(A)
Hej.
har kört fast med denna uppgift i flera timmar och inget av det jag tror är logiskt blir rätt trots att den verkar ganska enkel och jag har väldigt många punkter som berättar väldigt mycket.
och sen en annan sak. Läste om att bestämma a-koefficienten genom att skriva i faktorform som f(x) = k(x-x1)(x-x2)…(x-xn) som jag ritat ut i blått men här fungerar det inte heller.. är det för att det bara finns ett nollställe?
”En hängbro består av pelare, pyloner, med hängkablar mellan sig som i sin tur bär upp själva bron. Golden gate-bron i San Francisco, USA, är en av världens längsta hängbroar.
Brons pyloner är 160 meter höga, mätt från körbanan, och sträckan mellan pylonerna, huvudspannet, är 1280 meter.
Bestäm algebraiskt en andragradsfunktion för hängkabeln som håller upp huvudspannet. Räkna med att hängkabeln hänger ända ned till körbanan.”
Symmetrilinjen är x=640 och vertex = (640,0) varför
y = k(x-640)^2
160 = y(0) = k*640^2 viket ger k=160/640^2
Alltså: y = 160/640^2(x-640)^2
Trinity2 skrev:Symmetrilinjen är x=640 och vertex = (640,0) varför
y = k(x-640)^2
160 = y(0) = k*640^2 viket ger k=160/640^2
Alltså: y = 160/640^2(x-640)^2
Hm. Vi börjar från början. Var det korrekt att använda sig av faktorform alltså? Även om jag inte har två nollställen och en tredje punkt. Hemsidan Eddler är lite otydlig med det och boken jag har beskriver aldrig en sådan metod.
sedan tycker jag att faktorformen med ett nollställe egentligen inte ger något andragradspolynom. Hur resonerar du när du kvadrerar i slutet? Kan inte resonera fram det från Eddler (vet inte hur reglerna ser ut med att länka så jag väljer urklipp):
Men är det alltså korrekt uppfattat att varför mina xs = -(p/2) = 640 och dyl. logik inte stämmer är för att jag måste se funktionsuttrycket ur ett ax^2 + bx + c och hitta metoder för att räkna ut andragradskoefficienten (a)?
En person som inte kunde säga mer i ett annat sammanhang om uppgiften tidigare att jag skulle räkna ut den tredje koordinaten vilket är (1280, 160) och utgå från de tre koordinaterna för att lösa uppgiften. Menar personen på ytterligare sätt?
tack på förhand
EDIT: som en blixt ur klar himmel. Du tänker alltså x1 = x2 = 640?:) Då ser jag din kvadrat
sorry dubbelpost. Gick inte ta bort och råkade citera; inte redigera. (Alltså citera mig själv i ett svar).
EDIT: tror nog det heter koefficienten till variabeltermen av andra graden och inte andragradskoefficienten.. viktigt att ha tungan rätt i mun i dessa sammanhang:)
sorry gjorde det igen(!) trött idag. Alltså citera ist för redigera
åt rätt håll kanske om man ser till grafen men inte riktigt
Trinity2 skrev:Alltså: y = 160/640^2(x-640)^2
Spot on!
förstår verkligen matte bättre med det här exemplet. Coolt. Koefficienten * funktionsuttrycket i faktorform. Förstår dock inte varför min senaste uträkning inte genererade samma sak. Ska klura på den..
maratmatorkin skrev:Trinity2 skrev:Alltså: y = 160/640^2(x-640)^2
Spot on!
förstår verkligen matte bättre med det här exemplet. Coolt. Koefficienten * funktionsuttrycket i faktorform. Förstår dock inte varför min senaste uträkning inte genererade samma sak. Ska klura på den..
Du kan räkna som du tänker och du förflyttar kurvan -160 steg.
f(x) = k (x-0)(x-1280) = kx(x-1280)
där f(640)=-160 vilket ger k=1/2560=160/640^2
Men sedan får du flytta upp kurvan igen +160 och får
f(x) = 160/640^2 x(x-1280)+160
som kan förenklas
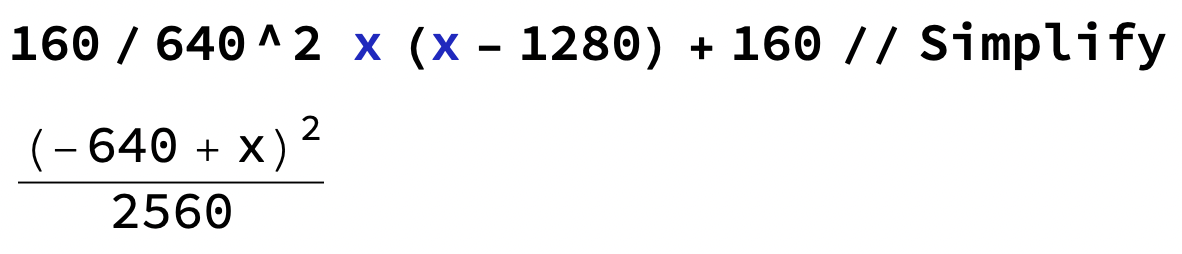
vilket är det samma som
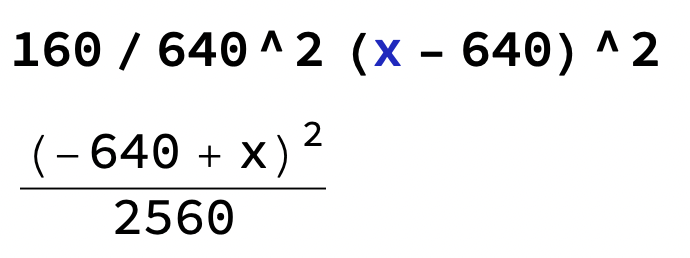
När en andragradskurva tangerar ett nollställe säger man att nollstället har "multipliciteten 2" och det kan som du riktigt skriver anges som
k(x-x1)(x-x2)
där x1=x2 varför man får
k(x-x1)^2
Ah, det är det multiplicitet betyder i sådana här sammanhang…! Jag har av någon anledning aldrig riktigt begripit vad det innebär.
Läggdags. Tack för alla svar. Återkommer (I’ll be back)😎
naytte skrev:Ah, det är det multiplicitet betyder i sådana här sammanhang…! Jag har av någon anledning aldrig riktigt begripit vad det innebär.
AI ger ett rätt trevligt svar, om något begränsat;
Jag vet inte varför denna term inte ingår i matematikkurserna. Man talar nog hellre om "dubbelt nollställe" eller liknande. Termen är inte så svår och borde ingå IMO.
Här är dock en utförligare sida
https://en.wikipedia.org/wiki/Multiplicity_(mathematics)
Dock är den nog lite för "torr" och abstrakt för TS och Ma2, men några av raderna kanske man kan ta till sig.
Trinity2 skrev:naytte skrev:Ah, det är det multiplicitet betyder i sådana här sammanhang…! Jag har av någon anledning aldrig riktigt begripit vad det innebär.
AI ger ett rätt trevligt svar, om något begränsat;
Jag vet inte varför denna term inte ingår i matematikkurserna. Man talar nog hellre om "dubbelt nollställe" eller liknande. Termen är inte så svår och borde ingå IMO.
Här är dock en utförligare sida
https://en.wikipedia.org/wiki/Multiplicity_(mathematics)
Dock är den nog lite för "torr" och abstrakt för TS och Ma2, men några av raderna kanske man kan ta till sig.
TS approves
Nu kan jag passa på att smöra för min lärare🙈😈
Trinity2 skrev:maratmatorkin skrev:Trinity2 skrev:Alltså: y = 160/640^2(x-640)^2
Spot on!
förstår verkligen matte bättre med det här exemplet. Coolt. Koefficienten * funktionsuttrycket i faktorform. Förstår dock inte varför min senaste uträkning inte genererade samma sak. Ska klura på den..
Du kan räkna som du tänker och du förflyttar kurvan -160 steg.
f(x) = k (x-0)(x-1280) = kx(x-1280)
där f(640)=-160 vilket ger k=1/2560=160/640^2
Men sedan får du flytta upp kurvan igen +160 och får
f(x) = 160/640^2 x(x-1280)+160
som kan förenklas
vilket är det samma som
När en andragradskurva tangerar ett nollställe säger man att nollstället har "multipliciteten 2" och det kan som du riktigt skriver anges som
k(x-x1)(x-x2)
där x1=x2 varför man får
k(x-x1)^2
Finns en annan väg också med ekvationssystem. :)
Förstår inte riktigt hur vi kom in på det du skriver om men löste det nu när jag tänkte mer abstrakt och sen såg jag felet vilket jag även gjorde i räknaren vilket var att jag inte räknade konstanten i polynomet som en egen term och delade aldrig den med 640. Nu fick jag b = -0,5 :)
riktigt kul och många aha-upplevelser.
vad är det för mjukvara du demonstrerar beräkningarna på? Cool font.
Klarmarkerar nog sen.:) tack!
maratmatorkin skrev:Trinity2 skrev:maratmatorkin skrev:Trinity2 skrev:Alltså: y = 160/640^2(x-640)^2
Spot on!
förstår verkligen matte bättre med det här exemplet. Coolt. Koefficienten * funktionsuttrycket i faktorform. Förstår dock inte varför min senaste uträkning inte genererade samma sak. Ska klura på den..
Du kan räkna som du tänker och du förflyttar kurvan -160 steg.
f(x) = k (x-0)(x-1280) = kx(x-1280)
där f(640)=-160 vilket ger k=1/2560=160/640^2
Men sedan får du flytta upp kurvan igen +160 och får
f(x) = 160/640^2 x(x-1280)+160
som kan förenklas
vilket är det samma som
När en andragradskurva tangerar ett nollställe säger man att nollstället har "multipliciteten 2" och det kan som du riktigt skriver anges som
k(x-x1)(x-x2)
där x1=x2 varför man får
k(x-x1)^2
Finns en annan väg också med ekvationssystem. :)
Förstår inte riktigt hur vi kom in på det du skriver om men löste det nu när jag tänkte mer abstrakt och sen såg jag felet vilket jag även gjorde i räknaren vilket var att jag inte räknade konstanten i polynomet som en egen term och delade aldrig den med 640. Nu fick jag b = -0,5 :)
riktigt kul och många aha-upplevelser.
vad är det för mjukvara du demonstrerar beräkningarna på? Cool font.
Klarmarkerar nog sen.:) tack!
Programmet heter Mathematica.
Trinity2 skrev:maratmatorkin skrev:Trinity2 skrev:maratmatorkin skrev:Trinity2 skrev:Alltså: y = 160/640^2(x-640)^2
Spot on!
förstår verkligen matte bättre med det här exemplet. Coolt. Koefficienten * funktionsuttrycket i faktorform. Förstår dock inte varför min senaste uträkning inte genererade samma sak. Ska klura på den..
Du kan räkna som du tänker och du förflyttar kurvan -160 steg.
f(x) = k (x-0)(x-1280) = kx(x-1280)
där f(640)=-160 vilket ger k=1/2560=160/640^2
Men sedan får du flytta upp kurvan igen +160 och får
f(x) = 160/640^2 x(x-1280)+160
som kan förenklas
vilket är det samma som
När en andragradskurva tangerar ett nollställe säger man att nollstället har "multipliciteten 2" och det kan som du riktigt skriver anges som
k(x-x1)(x-x2)
där x1=x2 varför man får
k(x-x1)^2
Finns en annan väg också med ekvationssystem. :)
Förstår inte riktigt hur vi kom in på det du skriver om men löste det nu när jag tänkte mer abstrakt och sen såg jag felet vilket jag även gjorde i räknaren vilket var att jag inte räknade konstanten i polynomet som en egen term och delade aldrig den med 640. Nu fick jag b = -0,5 :)
riktigt kul och många aha-upplevelser.
vad är det för mjukvara du demonstrerar beräkningarna på? Cool font.
Klarmarkerar nog sen.:) tack!
Programmet heter Mathematica.
Intressant. Tack!
