Gränsvärde
Jag förstår inte hur svaret kan bli oändligheten. Jag får de till noll! Var tänker jag fel?
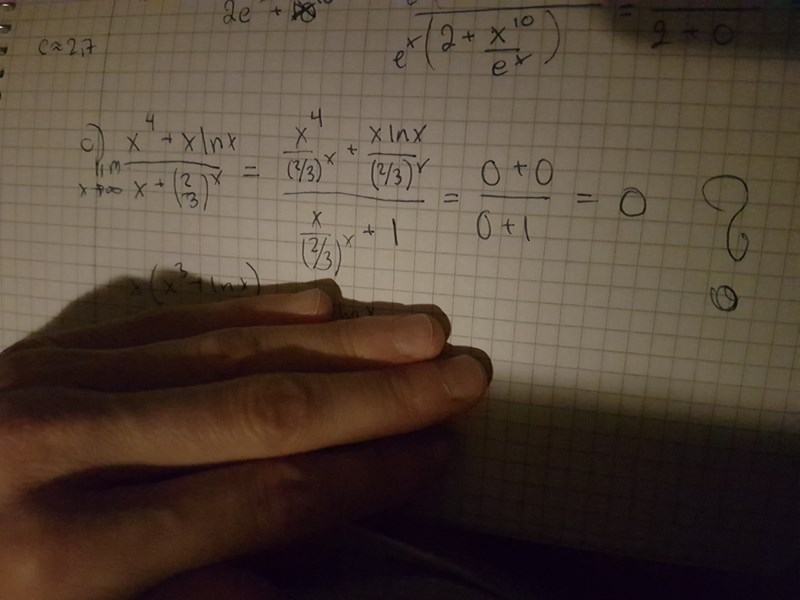
Eftersom växer mycket snabbare än och går mot 0 när x går mot oändligheten, går uttrycket mot som går mot oändligheten.
Hej!
bara om . Annars går det mot 0, är du med på det?
Moffen skrev:Hej!
bara om . Annars går det mot 0, är du med på det?
Åhh de stämmer, kom inte ihåg det trots att jag precis läst om de :-(
Tack! :-)
Det positiva talet blir mindre och mindre ju större det positiva talet är; därför kommer nämnaren att bli alltmer lik ju större är, så att kvoten blir mer och mer lik ju större är.
Både och blir större och större ju större är, så det sökta gränsvärdet existerar inte i egentlig mening; man brukar skriva att det är det oegentliga gränsvärdet , men tänk på att inte är ett tal som man kan "närma sig".


