Gränsvärde med taylor
Hej!
Kan någon snälla förklara vad som händer i lösningen?
Förstår inte steget jag har strukit under med rött. Tänkte att de kanske bara bröt ut 2x^2, men det ser inte ut så.
Förstår inte heller vad som händer med exponenten, hur den bara "försvinner"?
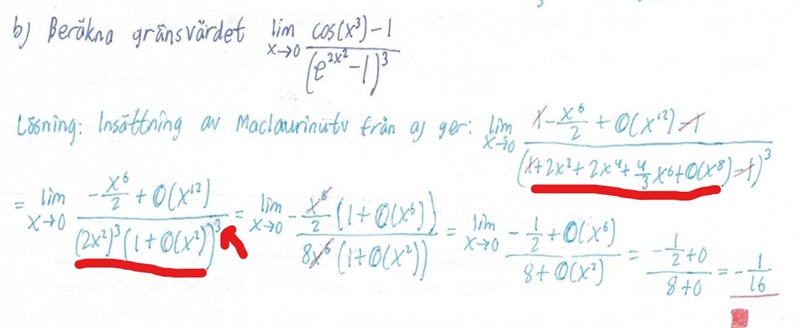
Väldigt tacksam för svar!!
, alla exponenter som är 8 och över bakas in i alla andra ordo.
Pikkart skrev:, alla exponenter som är 8 och över bakas in i alla andra ordo.
Leden men jag fattar inte riktigt. Är det såhär nämnaren förenklas?:
=
"Äter" ordot upp de röda termerna så att det blir kvar?
Uttrycket blir därför när x går mot noll.
Kom ihåg att vilket är större än ditt ordo, det försvinner alltså in där, självklart samma sak med de som har större exponenter.
Pikkart skrev:
Uttrycket blir därför när x går mot noll.
Varför käkas inte upp? Är det bara för att man måste ha något kvar att räkna med? Så man väljer vilka som äts upp?
Edit: Ledsen men jag fattar verkligen inte hur du kommer fram till det rödmarkerade, kan du snälla förklara?
Alla termer som är lika stora eller större än ordotermen äts upp, de resterande kan du fortfarande räkna på. Om du vetenskapligt är nyfiken på varför den gör det så får nog någon annan rycka in, jag har inte pluggat envarren på 5 år.
Tack så mycket för hjälpen, nu förstår jag!!



