2
svar
47
visningar
Fysiker90 är nöjd med hjälpen
Green's formel
Hejsan!
jag har följande tal: där är cirkeln
Facit till uppgiften är som följande: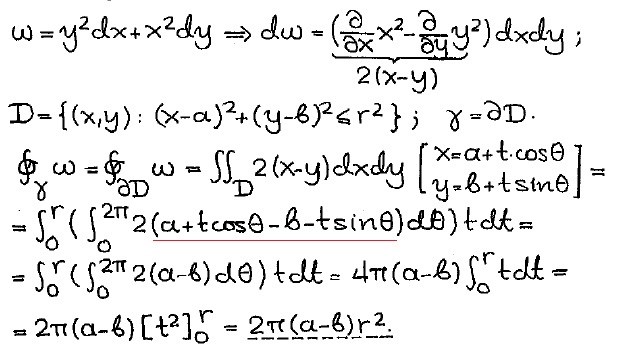 Jag fårstår inte det understruckna, hur försvinner.
Jag fårstår inte det understruckna, hur försvinner.
Misstänker det är någon trigonometrisk formel som används men inte vilken.
Skulle uppskatta om hjälp så jag kan förstå denna lösning.
Tack på förhand!
Integralen över en hel period (hela cirkeln) är ju noll. Detsamma gäller
Du kan också se det som att medelvärdet av är eller att det ligger lika mycket area under som över kurvan osv.
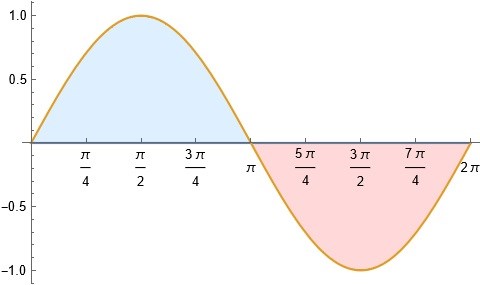 Arean av det blå området är lika stor som arean av det rosa området.
Arean av det blå området är lika stor som arean av det rosa området.
Nu när du nämner det kommer det tillbaka för mig, tack!

