Gymnasiematematik: vilken metod används för att räkna division av bråk?
Hej,
Ni som jobbar som lärare i matematik på gymnasiet eller ni som går på gymnasiet, vilken metod lärs ut vid division av bråk?
I boken som mina elever räknar i (åk 8) används metoden med minsta gemensamma nämnare. Är det värt att lära ut den metoden eller kommer metoden med invers vara den primära metoden högre upp i åldrarna?
Tänker att eleverna kanske blir förvirrade av att lära sig båda metoderna? Eller har någon av er en bra förklaring för hur man kan koppla ihop de båda metoderna?
(Lärare på gymnasiet)
Jag tror det är bäst om du ger exempel på metoderna du vill jämföra och hur de presenteras.
Utifrån ett läroplansperspektiv så utgår gymnasiets läroplaner från att eleverna vet hur man tolkar och mekaniskt utför bråkdivisioner. Så vi lär inte ut något i teknisk mening, bara repeterar ytligt algoritmerna de förväntas ha mött i grundskolan.
Rent som en beräkningsteknik gör vi i mina kurser (i bok och på tavlan) uteslutande bråkdivision med mönstret
vilket jag skulle kalla "med invers" där det "uppochnedvända bråket" d/c.
Däremot så är förlängning av bråk till gemensam nämnare helt ekvivalent med inversmetoden och kan vara ett sätt att motivera inversmetoden.
Min tolkning av "nämnar-metod"
Att lära sig bråk är ökänt svårt och det är nog inte att rekommendera att gå direkt till inversmetoden innan man förstått att bråkdivision representerar svar på frågor om proportioner eller ur många gånger en sak får plats i en annan osv. Att gå direkt till inversberäkningar kan vara lite riskfyllt.
Däremot så måste man i långa loppet internalisera effektiva tekniker för att kunna automatisera sitt tänkande kring de enkla problemen och inversmultiplikation är effektivt snabbast så att läsa sig mönstret är ett måste.
SeriousCephalopod skrev:(Lärare på gymnasiet)
Jag tror det är bäst om du ger exempel på metoderna du vill jämföra och hur de presenteras.
Utifrån ett läroplansperspektiv så utgår gymnasiets läroplaner från att eleverna vet hur man tolkar och mekaniskt utför bråkdivisioner. Så vi lär inte ut något i teknisk mening, bara repeterar ytligt algoritmerna de förväntas ha mött i grundskolan.
Rent som en beräkningsteknik gör vi i mina kurser (i bok och på tavlan) uteslutande bråkdivision med mönstret
vilket jag skulle kalla "med invers" där det "uppochnedvända bråket" d/c.
Däremot så är förlängning av bråk till gemensam nämnare helt ekvivalent med inversmetoden och kan vara ett sätt att motivera inversmetoden.
Min tolkning av "nämnar-metod"
Att lära sig bråk är ökänt svårt och det är nog inte att rekommendera att gå direkt till inversmetoden innan man förstått att bråkdivision representerar svar på frågor om proportioner eller ur många gånger en sak får plats i en annan osv. Att gå direkt till inversberäkningar kan vara lite riskfyllt.
Däremot så måste man i långa loppet internalisera effektiva tekniker för att kunna automatisera sitt tänkande kring de enkla problemen och inversmultiplikation är effektivt snabbast så att läsa sig mönstret är ett måste.
Här sker nog ett skrivfel;
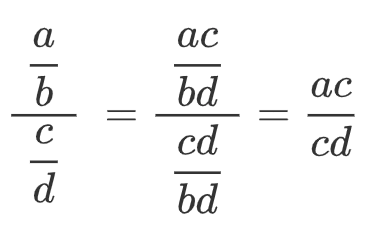
(Lärare i högstadiet)
Jag kan möjligen visa metoden med gemensam nämnare för att på något sätt visa varför eller hur det fungerar, för att vissa elever har ett behov av att få veta det och att det är bra om man ska studera matematik på ett djupare plan längre fram.
Jag går dock ganska snabbt vidare till att visa "inverteringsmetoden". För att göra beräkningar är det effektivast och det som jag själv använder när jag ska beräkna division av bråk. Det brukar de flesta ha ganska enkelt att ta sig till. Merparten av eleverna vill ha en metod som de kan lära sig så enkelt som möjligt och kan använda för att lösa de uppgifter som de behöver i skolan för att klara ett visst betyg. Det stämmer också ganska bra överens med hur det fungerar i verkligheten, att man väljer den enklaste och snabbaste metoden för att göra något. Min bild är även att det är så på gymnasiet.
Däremot är det viktigt att eleverna förstår vad ett bråk är och hur man hanterar bråk, också för att kunna hålla isär metoderna för att addera, subtrahera, multiplicera och dividera bråk.
För att arbeta lite med förståelse så tycker jag det är bättre att exempelvis också visa "Bråktavlan" för vissa beräkningar för att få en förståelse för hur man gör. Exempelvis (1/2)/(1/4) att man då kan förklara att det betyder hur många fjärdedelar som får plats i en halv och då kan man se på bråktavlan att det är 2 stycken.
Använder ni XYZ-boken? Vi använder också den och de kör enbart att göra om till gemensam nämnare, vilket är lite dumt. Så jag utgår oftast inte från den när jag går igenom det, men nämner för eleverna att de visar ett "lite längre sätt" men som i grunden är samma sak.



