Har jag parametriserat denna yta rätt?
Halloj!
Jag satt med frågan nedan:
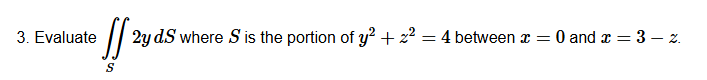
Jag införde en paramtetrisering där och . Då avbildas ytan på området . Då kan vi skriva om integralen enligt:
Sättet jag kom fram till min parametrisering på var att jag ritade upp en hel cylinder:
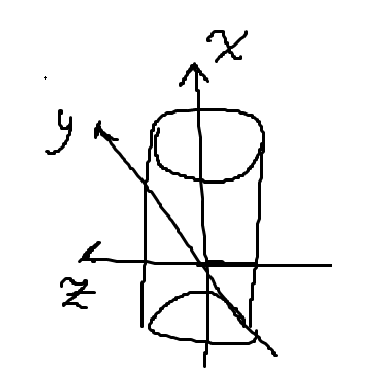
och sedan tänkte jag att vinkeln ska gå från till , så att vi täcker ett helt varv, samt att går från "botten av cylindern" (höger sida i bilden jag har ritat) till "toppen som begränsas av planet .
Är det korrekt uppställt och resonerat? Det som är krångligast är att få till rätt parametrisering men jag tror att jag lyckades.
EDIT: eller nej, detta blir nog fel. Jag vill ju inte ha punkter inuti cylindern, men detta får jag väl då jag låter variera som jag har gjort? Det kanske är mer naturligt att låta variera?
Jag har för mig att används som basvektorn i x-ledet, i y-ledet och i z-ledet. Parametriseringen som du skrivit skulle då motsvara en del av cylinderytan längs -axeln.
, där och skulle ge cylinderytan längs -axeln.
Japp, ser det nu! Nu när jag kollar på min figur igen fattar jag inte hur jag såg fel... Haha
Men bara för att vara tydlig, i det här fallet är ett ytelement, inte sant? Det vill säga, vi vill integrera över ytan i rummet och inte över området som begränsas av ?
Ja, är ytelement och man håller på med att beräkna en ytintegral.
Men går det att veta att detta är en ytintegral utan att någon säger explicit att det är det? Jag tänker att med tanke på att det är symbolen är det rimligt att det har med (yt)area att göra. Liksom hur vet man vilken typ av integral det ska vara?
Och en fråga till:
Ett areaelement är ju sådant att det har infinitesimala mått som är parallella med koordinataxlarna. Hur utvidgar man den definitionen till 3D? Ett ytelement kan väl inte också ha mått som är parallella med koordinataxlarna?
Uppgiften säger att " is the portion of ..." och man ska beräkna .
Denna ekvation beskriver en yta i rummet, så man ska integrera över ytan.
Ytelement är en "infinitesimal parallellogram" i xyz-rummet. Det finns ingen anledning att kräva att parallellogrammen är en rektangel parallell med koordinatplanen / -axlarna.
Men om ytan böjer sig måste väl ytelementet också göra det, dvs. det kan inte vara tvådimensionellt?
Är ett kurvelement ds som ingår i en krökt kurva en- eller tvådimensionell?
Endimensionellt givetvis. Jag uttryckte mig slarvigt. Det jag menade men inte lyckades fatta i ord var: är det verkligen ett parallellogram om det är krökt? Liksom om man kröker en rektangel tillräckligt mycket blir det ju en cylinder.
Tillägg: 20 aug 2025 20:10
Men jag har funderat vidare och det är rimligt att det fungerar. Låt säga att vi skapar ett litet areaelement i vår parametervärld (låt säga parametrar och ). Då avbildas detta på något som är infinitesimalt nära ett parallellogram med area



