Har jag tänkt rätt här? Mekanik - maximal hastighetskomposant utan friktion
Halloj!
Jag sitter med uppgiften nedan från en gammal dugga:
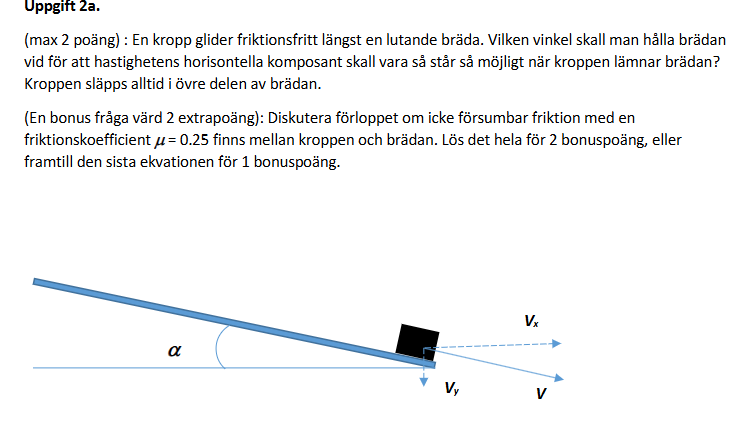
Jag tänker att accelrationens storlek nedför planet enligt känt resultat ges av . Jag tänker att accelerationen går att komposantuppdela, och genom lite trigonometri kan vi lista ut att accelerationens storlek horisontellt (om vi skriver in allt i ett klassiskt, kartestiskt koordinatsystem) ges av .
Vi vill alltså maximera accelerationen , vilket i slutändan ger en så stor hastighet i horisontell led möjligt. Vi deriverar med avseende på och söker nollställen:
Vinkeln är alltså .
Jag bara undrar om jag har gjort rätt här.
Jag tror att det är fel resonerat. Du ska maximera vx, inte ax. vx måste bero på hur lång sträcka som accelerationen i x-led verkar. Och sträckan måste på nåt sätt bero på vinkeln (har inte riktigt tänkt klart känner jag....).
Jag gjorde istället ett energiresonemang.
mgh=(mv^2)/2
v=vx/cosa
h=Lsina. (L är planets längd, vilket är en konstant)
Men om accelerationen är maximal så kommer väl även hastigheten vara maximal i slutändan (eftersom hastigheten skalar linjärt med accelerationen, enligt och alltså .
Tillägg: 26 apr 2025 23:38
Aha, jag fattar nu.
Beroende på vinkel så glider klossen olika länge och det påverkar också hastigheten!
Precis! Jag tror att man kommer fram till rätt samband som med energiresonemang, om man tecknar
- a som funktion av vinkeln
- sluthastigheten som funktion av a och planets längd
- xkomposanten av sluthastigheten
Jag ska försöka lösa den med ett energiresonamng och den mekaniska energins bevarande som du föreslog, men jag skulle också vilja testa att lösa den rent "mekanististk" eller vad man ska säga, med explicita funktioner för acceleration, hastighet och sträcka... om det är möjligt?
Vi kan ju skriva upp några ekvationer:
Jag tänker att begynnelsevillkoren vid i fallet för hastigheten blir och .
Vi borde kunna säga att vid är , där betecknar brädans längd. Vi löser ut och stoppar in denna i hastighetsfunktionen, tar fram den horistontella komposanten och maximerar med avseende på .
Det fungerade! :D
Jag fick rätt svar
Grejt!
Det brukar bli lite mer "direkt" resonemang att räkna på mekaniska energier, om man inte är intresserad av tiden. Att gå via rörelseekvationerna brukar då bli en liten omväg.
Visserligen, men på något sätt är det också skönt att kunna räkna med rörelse. Vill helst undvika att räkna på energibevarande för jag fattar inte vad energi är, så lite av princip vill jag inte använda det. Det är läskigt att använda något man inte förstår.
Rörelseekvationerna bygger ju bara på "längd" och "tid" och inga mystiska objekt som energi, så det är lättare att förstå vad som händer.
Och det tog inte så värst mycket tid med rörelseekvationerna heller. Tog ganska exakt fem minuter. Det kan det vara värt i utbyte mot att förstå vad man räknar på.
En del algebra men det sitter i ryggmärgen vid det här laget.
Nu när jag testar ett energiresonemang blir det faktiskt nästa exakt samma beräkning, så det var nog ungefär lika "enkelt". Om man sätter erhåller man till slut:
och det var precis denna ekvation jag löste också med rörelseekvationerna!
naytte skrev:Nu när jag testar ett energiresonemang blir det faktiskt nästa exakt samma beräkning, så det var nog ungefär lika "enkelt". Om man sätter erhåller man till slut:
och det var precis denna ekvation jag löste också med rörelseekvationerna!
Det var precis vad jag var påväg att säga. Eliminera tiden i rörelseekvationerna, så får du "energiprincipen"
Det hade snarare varit väldigt otillfredställande om man hade kommit fram till olika resultat.
Och det tog inte så värst mycket tid med rörelseekvationerna heller. Tog ganska exakt fem minuter. Det kan det vara värt i utbyte mot att förstå vad man räknar på.
Vissa uppgifter är tyvärr olösbara utan energiresonemang. Och jag undrar lite på vad mer är det du behöver i form av energihärledning än den via ? Tycker den är ganska snäll. Det är coolt att se hur kraftfull Newtons andra lag är. Att använda lagrangeekvationen är också är väldigt häftigt. Vet du när ni kommer att börja göra det?
Men det är lätt att vara aktivistisk och ha principer, när det inte kostar nåt (dvs om man ändå får rätt svar menar jag). Jag tycker du kan använda begreppet energi, utan att egentligen veta vad det är. Se energibegreppet som ett enklare sätt att räkna när man rör sig i ett kraftfält av något slag.
Som mrP säger. Du kommer inte att slippa undan...
Vad är det för härledning med hjälp av Newton II du hänvisar till, MrP? Skulle vara intressant att se denna. Annars tror jag att jag behöver bättre mattekunskaper innan jag kan acceptera detta ordentligt. Kan visserligen ANVÄNDA energibevarande om jag så måste men jag vill helst förstå det också. Egentligen vill jag förstå Noethers sats och matematiken bakom denna innan jag kan ta mig vidare och titta på de bevarade storheterna. De härledningar av hennes sats jag har sett ser dock skräckinjagande ut.
Som mrP säger. Du kommer inte att slippa undan...
😬😬😬
Vänta lite nu...
Nu när jag läser om Noethers sats så hänvisas det till "the lagrangian" för ett system. Är detta inte ett objekt som är definierat med hjälp av begreppet energi?
Det var inget.
Jag hittade en härledning utifrån som visade att "" är konstant över tid, alltså har tidsderivata .
Det räcker för min del.
naytte skrev:Vad är det för härledning med hjälp av Newton II du hänvisar till, MrP? Skulle vara intressant att se denna.
Man kör lite fysikerknep för lösning av sep.diffekv, som jag dock vet du gillar ;) för man slirar med differentialerna, enligt:
Är detta inte ett objekt som är definierat med hjälp av begreppet energi?
Det stämmer. Det första steget ovan är nog vad man anser att är definitonen av kinetisk energi. Det intressanta med Lagrangeekvationen är att man kan härleda Newton II baklänges med den och att den möjliggör väldigt effektiva lösningar av annars väldigt svåra, ev olösliga, mekaniska problem, se dubbelpendulum.
Den där härledningen härledningen av kinetisk energi gör mig extremt lycklig.
Jag hittade som sagt en härledning som var väldigt tillfredsställande angående påståendet att "storheten":
bevaras över tid. Det räcker faktiskt.
Det är fortfarande lite mystiskt vad det är som bevaras (och det slutar mejka lika mycket sense när man kommer ned på molekylnivå som man ofta gör i kemin) men för mina mekanikändamål räcker det gott och väl för min del att:
(1) definiera en storhet
(2) Visa att
Att använda är generellt tillfredsställande. Det känns som man ger matematiker fingret när man använder den metoden. Och det känns ju alltid jättebra.
Blir det verkligen maximal horisontell hastighet vid 45 graders vinkel och ingen friktion?
Jan Ragnar skrev:Blir det verkligen maximal horisontell hastighet vid 45 graders vinkel och ingen friktion?
Näe. Jag tror att naytte ganska snabbt insåg att hans ansats i trådstarten var fel.
Det är fortfarande lite mystiskt vad det är som bevaras (och det slutar mejka lika mycket sense när man kommer ned på molekylnivå som man ofta gör i kemin) men för mina mekanikändamål räcker det gott och väl för min del
Precis min inställning! Det spelar ingen större roll vad man kallar något, huvudsaken det kan användas till nått nyttigt.
(The engineering approach)
Jag har blivit för matematikerpilled på senaste tror jag. Måste gå tillbaka till ingenjörskonstens första huvudsats: if it's close enough, it's good enough
Nu när du ändå är igång kan du försöka härleda . Tips: . Det är rörelsemängd om du glömt.
Är det inte bara att integrera med avseende på tid?
Jo, eller hela F.
Visst är rörelsemängd också en storhet som bevaras enligt Noethers sats?
Jag hittade en lång videoserie om denna där snubben som snackar verkar ta allting från grunden (definiera "the lagrangian" och bygga allt därifrån), så jag ska ta några timmar nu under "självstudierna" som börjar på onsdag och sluka den. Förhoppningsvis hjälper det.
Precis, rörelsemängd bevaras pga translationsinvarians i rummet. Alltså, egenskaperna är densamma oavsett var vi är i rummet.





