Härled klotets volym mha integraler (Matematik/Matte 4/Integraler och tillämpningar)

Borde jag anväda pythagora's sats ?

Jag vet inte vad jag bör döpa basen till?

Ja, pythagoras eller cirkelns ekvation. Det är vilket som.

$x^{2} + y^{2} = r^{2}$

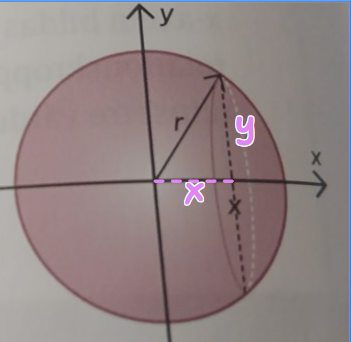
Aha, jag trodde hela höjden var x.

Det finns säkert fler sätt att komma till samma resultat. Så är det ofta.

roterar den runt x-axeln ?

Ja, det är så jag spontant skulle angripa problemet. En halvcirkel runt x-axeln från -r till r.

Lite snabbgoogling gav den här. Vet inte om det är samma: https://youtu.be/nHC92J8rNZs

hur får du fram -r och r ?

om jag använder pytrhagoras får jag

$x^{2} + y^{2} = r^{2} r = \pm \sqrt{x^{2} + y^{2}}$

Kanske man kan skriva integralen direkt så här:

Integranden är π * y²= π * (r²- x²)
som ska integreras över x från -r till +r

vilket ger

Och här fastnade jag när jag försökte skriva integralen FINT
men det får läsaren kanske göra själv...

Nu gick det:

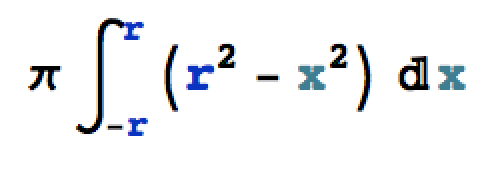
Jo, men du vill ha en funktion av x istället.

y²=r²-x²

Sedan är arean av skivorna A(x)=pi*y².

Det är det du skall integrera längs x-axeln, från -r till r.

Kommer du vidare?

Tillägg: 20 feb 2026 21:57

Alltså vad Arktos precis skrev.

Jag betraktar y² som en funktion av x

eller så här y(x)² = r²- x² om vi håller oss till den övre halvcirkeln
aå funktionen blir entydig. Jag tycker videon var lite krånglig.

Är det för okonventionellt?

Det finns många olika sätt man kan angripa ett problem som dessa på, och alla är lika bra så länge man förstår vad man sysslar med. Insikten är att man kan dela upp volymen "i oändligt små (infinitesimala) bitar" och sedan summera alla dessa bitar. Informellt är det detta vi menar med integrering. Nedan följer några exempel på hur man kan göra:

Lösningsförfarande 1

Vi inser att ett klot av radie $r$ erhålles då vi roterar $y=\sqrt{r^2-x^2}$ runt $x$ -axeln. För att beräkna volymen som då alstras kan vi dela in området under kurvan i rektanglar med infinitesimal bredd $dx$ och höjd $y$ :

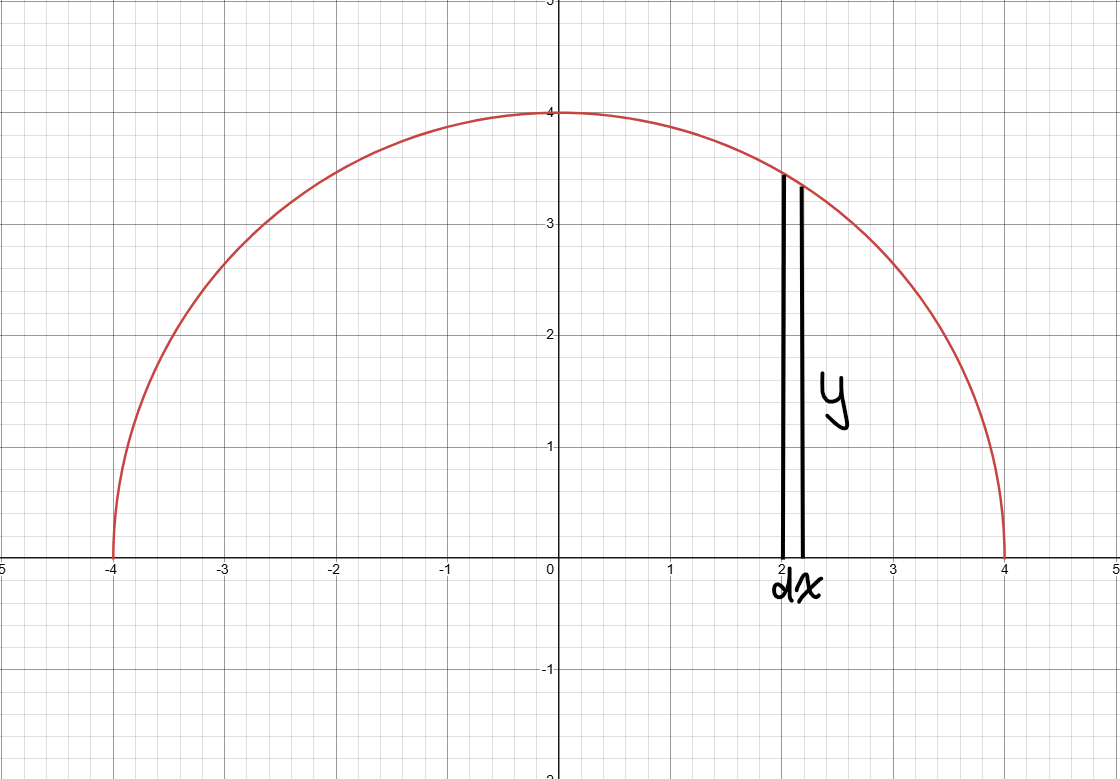
Rektangeln är överdrivet bred av illustrativa skäl. Om vi roterar en sådan rektangel runt $x$ -axeln erhåller vi en disk . En sådan disk har infinitesimal volym $dV(x,dx)=\pi y^2dx$ . För att beräkna volymen summerar vi alla dessa små volymer över det aktuella intervallet:

$\displaystyle V=\sum_{-r}^{r}dV=\pi\int_{-r}^{r}y^2dx=\pi \int_{-r}^{r}\left(r^2-x^2\right)dx=\frac{4\pi r^3}{3}$

Lösningsförfarande 2

Vi hade kunnat genomföra ett liknande resonemang genom att rotera våra rektanglar runt $y$ -axeln istället. Då får man en ring med radie $x$ :

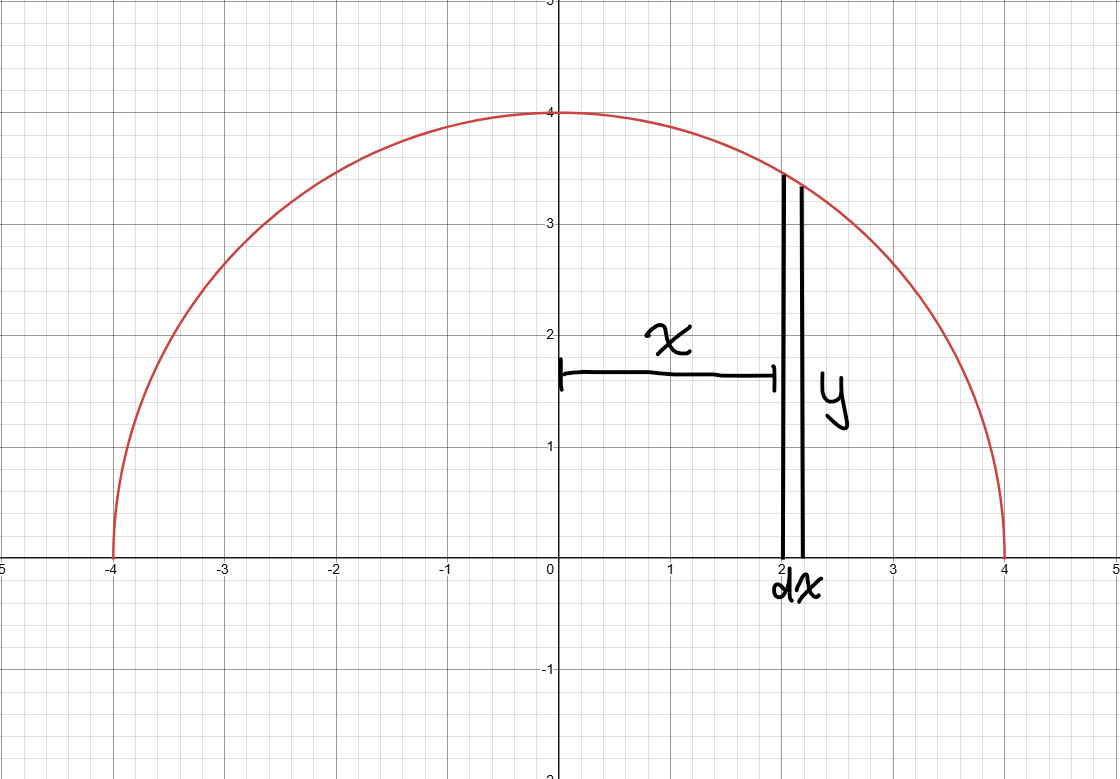
Om man "klipper upp" denna blir den till ett rätblock med volym $dV(x,dx)=2\pi x y dx$ . För att erhålla hela volymen summerar vi återigen, men multiplicerar denna gång med en faktor $2$ för att ta hänsyn till klotets undre halva. Notera att summeringsgränserna nu är annorlunda:

$\displaystyle V=2\sum_{0}^{r}dV=4\pi\int_{0}^{r}xydx=4\pi\int_{0}^{r}x\sqrt{r^2-x^2}dx=\frac{4\pi r^3}{3}$

*När jag skriver "rektangel", "ring" och "disk" avser jag egentligen former som är "oändligt nära" dessa. Detta innebär att volymen på formerna vi egentligen behandlar här är oändligt nära volymen på de riktiga formerna, vilket motiverar uttrycken för volymerna $dV$ . Om man arbetar formellt använder man knep för att komma runt detta, exempelvis gränsvärden, suprema och infima eller standarddelar om man går icke-standardvägen (min favorit).