Hastighetsprofil för Newtonsk fluid som strömmar laminärt mellan två parallella plattor

Hej!

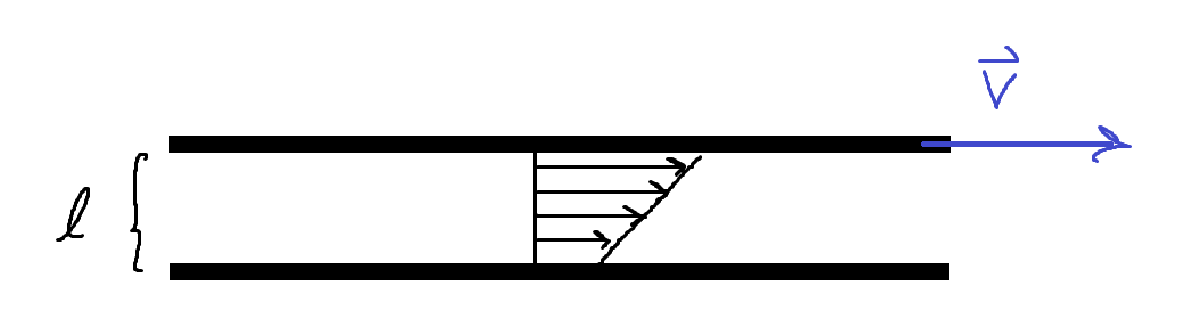
Jag försöker härleda ett explicit uttryck för hastighetsprofilen i en fluid som strömmar laminärt mellan två parallella plattor där strömningen induceras genom att den övre plattan rör sig med en hastighet $\mathbf{v}_\text{max}$ och den undre plattan är orörlig. Koordinatsystemet är lagt så att positiv $z$-riktning är rakt upp i bilden, positiv $y$-riktning är in i bilden och positiv $x$-riktning är rakt åt höger.

Vi börjar med att studera ett infinitesimalt fluidelement med infinitesimala sidlängder $\Delta x$, $\Delta y$ och $\Delta z$. Detta fluidelement kommer påverkas av fyra krafter i $x$-led:

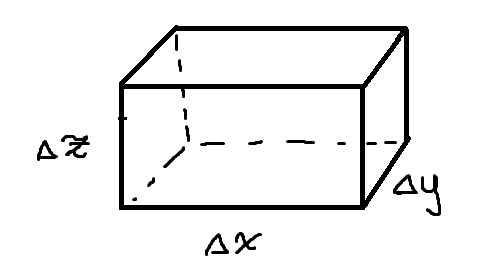
Alla tryck längs ytan längst till vänster vara infiniteismalt nära varandra (eftersom trycket är en kontinuerlig funktion i rummet). Vi väljer då något av dessa tryck $P$. Tryckkraften på den ytan är då infinitesimalt nära $P\Delta z\Delta y$. Tryckkraften på den motsatta ytan blir då, med infinitesimal noggrannhet $\left(P+\frac{\partial P}{\partial x}\Delta x\right)\Delta z\Delta y$. Låt skjuvspänningen i någon punkt på undersidan av elementet betecknas $\tau$. Då ges skjuvkraften på undersidan, med infinitesimal noggrannhet av $-\tau \Delta x\Delta y$. Skjuvkraften på ovansidan av fluidelementet ges då med infinitesimal noggrannhet av $\displaystyle \left(\tau+\frac{\partial \tau}{\partial z}\Delta z\right)\Delta x\Delta y$.

Enligt Newtons andra lag vet vi att summan av alla krafter i $x$-led måste vara noll. Således vet vi att

$\displaystyle 0=\sum F_x\approx\left(P-\left(P+\frac{\partial P}{\partial x}\Delta x\right)\right)\Delta z\Delta y+\left(-\tau+ \left(\tau+\frac{\partial \tau}{\partial z}\Delta z\right)\right)\Delta x\Delta y$

Efter förenkling ser vi att 

$\displaystyle \frac{\partial P}{\partial x}=\frac{\partial \tau}{\partial z}$

Enligt Newtons viskositetslag vet vi dessutom att $\displaystyle \tau=\mu\frac{\partial v}{\partial z}$. Därför har vi att

$\displaystyle \frac{\partial^2 v}{\partial z^2}=\frac{1}{\mu}\frac{\partial P}{\partial x}$

Integrering två gånger med avseende på $z$ ger

$\displaystyle v\left(x,y,z\right)=\frac{z^2}{2\mu}\frac{\partial P}{\partial x}+C_1z+C_2$

No-slip villkoret för den undre plattan ger att $v\left(z=0\right)=0\implies C_2=0$ och för den övre plattan har vi

$\displaystyle v\left(z=\ell \right)=v_{\text{max}}\implies C_1=\frac{v_\text{max}}{\ell}-\frac{\ell}{2\mu}\frac{\partial P}{\partial x}$

Således har vi alltså profilen

$\displaystyle v\left(x,y,z\right)= \frac{z^2}{2\mu}\frac{\partial P}{\partial x}+ \left(\frac{v_\text{max}}{\ell}-\frac{\ell}{2\mu}\frac{\partial P}{\partial x}\right)z$

Är hastighetsprofilen jag har kommit fram till här korrekt? Den känns åtminstone rimlig eftersom den för ett fixt värde på $x$ och $y$ ger en hastighet som är minst i botten, högst i toppen och ökar monotont däremellan, vilket man förväntar sig (och som jag har alluderat till i figuren).