Högskoleprovet VT-19: lösningar
Denna tråd är tänkt att vara en samlingstråd för lösningarna till matematikdelen från vårens högskoleprov (6:te april 2019), för den som vill kontrollera sina egna lösningar, träna på tidigare uppgifter, eller är nyfiken.
Regler för tråden:
- Skriv av uppgiften i ord högst upp
- En uppgift per inlägg (om det inte är DTK och uppgifterna handlar om samma diagram/tabell/karta). (Detta medför att man lätt kan permalänka om man har frågor)
- Skriv upp svarsalternativen under frågan
- LaTeX-kod eller formeleditorn är att föredra när det kommer till formler och uträkningar
Om du vill ha fler förklaringar, läs gärna de gamla trådarna från HT18 och VT18.
x och y är udda tal. Vilket svarsalternativ är ett udda tal?
A:
B:
C:
D:
Välj två trevliga, udda tal, exempelvis fem och sju. Därefter går det troligtvis fortast att testa sig fram.
A: , ett udda tal, alltså är svaret A.
Svar: A, .
Johanna löste ekvationen felaktigt. Hon genomförde uträkningen i följande steg:
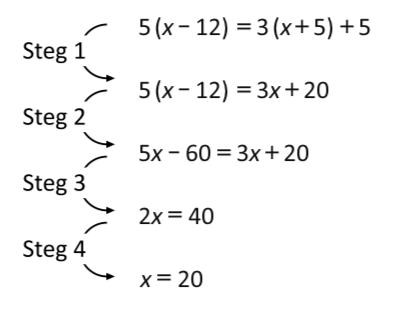
I vilket steg uppstod felet?
A: Steg 1
B: Steg 2
C: Steg 3
D: Steg 4
En annorlunda uppgift, men intressant. Vi provar att lösa ekvationen först:
Nu kan vi jämföra våra steg med Johannas, och konstatera att det är vid steg tre som det blivit knas.
Svar: C, Steg 3.
Vilket svarsalternativ motsvarar 15 procent av 70?
A:
B:
C:
D:
Femton procent, alltså femton hundradelar, är samma sak som . När detta multipliceras med 70 är det samma sak som att multiplicera täljaren, 15, med 70. Alltså är svaret D.
Svar: D,
ABCD är en rektangel och AFD är en triangel. Hur lång är DE?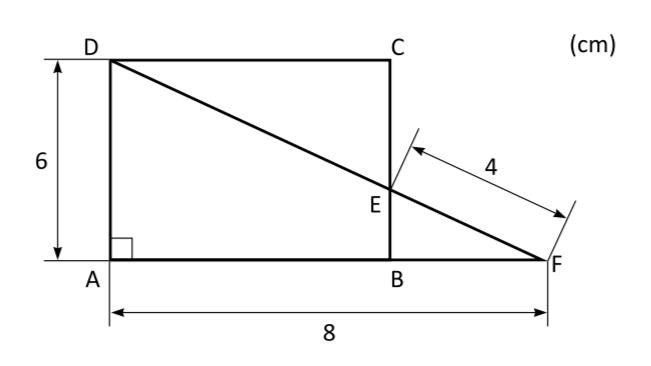
A: 5 cm
B: 6 cm
C: 7 cm
D: 8 cm
Det är lätt att börja tänka "likformighet", när denna typ av uppgifter kommer, men det är lönlöst i detta fall. När du ser en rätvinklig triangel, börja med att tänka "Pythagoras sats". Den ger oss nämligen att hypotenusan i den stora rektangeln, sträckan DF, är tio centimeter lång. Då måste sträckan DE vara (cm) lång.
Svar: B, 6 cm.
Vad är om ?
A: -5
B: 2,5
C: 3,5
D: 11
Sätt in värdet på x i uttrycket:
Om det är lättare kan x skrivas som 0,25. Förläng sedan hela bråket med fyra, för att bli av med den krångliga nämnaren. Då faller resultatet ut ganska naturligt:
Svar: A, -5.
Vad är m?
A: -1
B: 0
C: 1
D: 2
Sätt in i f(x). Då fås:
Alltså måste m vara lika med -1, för att påstående två ska stämma.
Svar: A, -1.
Claras och Alicias sammanlagda längd är 3,20 m. Alicias och Bedas sammanlagda längd
är 3,30 m. Den sammanlagda längden för alla tre är 4,80 m. Hur lång är Alicia?
A: 1,60 m
B: 1,65 m
C: 1,70 m
D: 1,75 m
Genom att använda bokstäverna A (Alicia), B (Beda) och C (Clara), kan sambanden ställas upp matematiskt:
Skillnaden mellan ekvation två och tre är 1,50 (meter). Den enda skillnaden mellan ekvation två och ekvation tre är Claras längd, och därför måste Clara alltså vara 1,50 meter lång. Denna uppgift kan vi sätta in i ekvation nummer ett, som säger att , och då få ut att . Alicia är alltså 1,70 meter lång.
Svar: C, 1,70 m.
Hur stor är vinkeln x?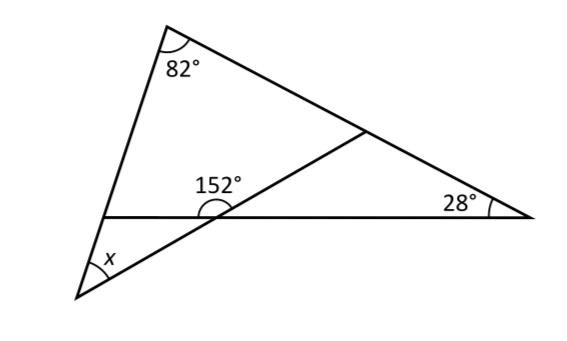 A: 28°
A: 28°
B: 32°
C: 38°
D: 42°
Genom att utnyttja att trianglarna överlappar varandra, kan vi konstatera att den blå vinkeln i bilden nedan är den vinkel vi kommer att behöva ta fram för att kunna beräkna x:
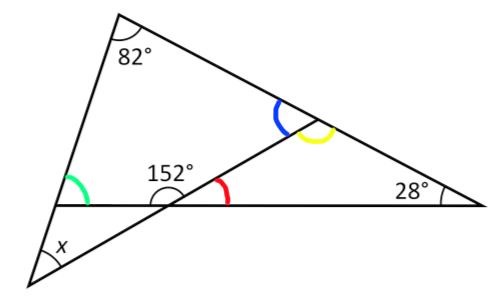
En triangel har alltid vinkelsumman 180 grader. Med hjälp av den uppgiften kan vi få fram att den grönmarkerade vinkeln är 70 grader stor. Vinkelsumman i en fyrhörning är alltid 360 grader, och då kan vi få fram att den blåa vinkeln är 56 grader. Slutligen kan vi då beräkna x, och få fram att x är 42 grader.
Svar: D, 42 grader.
För x, y och z gäller sambandet 3x-4y+2z=14. Vilket av svarsalternativen motsvarar detta samband?
A:
B:
C:
D:
Eftersom alla svarsalternativ har formen " x = (...) ", börja med att flytta alla termer förutom x-termen till högerledet:
Först och främst kan vi utesluta alternativ B, eftersom z ska vara negativt. Nu kan vi dividera båda led med tre, för att få ut x ensamt:
Här ifrån kan alternativ A också uteslutas, eftersom varken y-term eller z-term i A är dividerade med tre. Då kvarstår alternativ C och D. Eftersom tecknet framför 14 ska vara positivt, kan vi dra slutsatsen att svaret måste vara C.
Svar: C,
x och y är heltal sådana att . Vad är ett möjligt värde för ?
A: 10
B: 12
C: 18
D: 30
Gemensamt för de flesta högskoleprovsuppgifter är att det finns någon typ av knep man ska ta till. Vi kan börja med att skriva bråken med en gemensam nämnare, och se var det tar oss:
Hmm, vi kan nu prova att multiplicera täljare och nämnare med varandra, dvs. använda x = 5 och y = 6. Då får vi produkten 30, vilket är svarsalternativ D.
Svar: D, 30.
Vilket svarsalternativ visar grafen till funktionen h, där ?
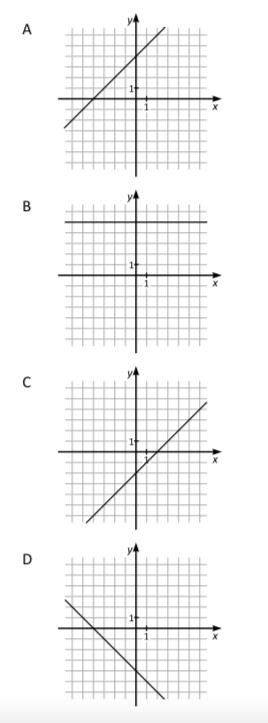
Vi kan börja med att beräkna h(x):
Så, k-värdet är ett. Alltså måste linjen gå uppåt, sett från vänster till höger. Det utesluter alternativ B och D. Dessutom ska m-värdet vara 4. Alltså kvarstår endast alternativ A.
Svar: A.
Vilket av svarsalternativen är lika med ?
A:
B:
C:
D:
Antingen kan man använda den potenslag som säger att , eller så skriver man ut talen:
Här ifrån kan vi möblera om lite och få:
Svar: A, .
Peter använder 50 % av sin månadspeng till att köpa godis. Stefan använder 30 % av sin månadspeng till att köpa godis. Den ena av dem köper godis för 35 kr mer än den andra.
Kvantitet I: Summan som Peter köper godis för
Kvantitet II: Summan som Stefan köper godis för
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Utan att veta vem som köper godis för 35 kr mer än den andra, går det inte att säga något om vilken kvantitet som är störst.
Svar: D, informationen är otillräcklig.
a är ett positivt heltal.
b är ett heltal.
Kvantitet I: a
Kvantitet II: ab
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
a är ett positivt heltal, alltså 1, 2, 3... Problemet kommer med b, som kan vara både positivt och negativt. För att avgöra dessa uppgifter snabbt är det bra att försöka hitta två fall som båda uppfyller kraven. Då vet vi att informationen inte räcker. Om a = 5 och b = -2, är ab = -10, och alltså är I större än II. Om däremot a = 5 och b = 4, är ab = 20, och II större än I. Därmed är informationen otillräcklig.
Svar: D, informationen är otillräcklig.
Kvantitet I: f(0)
Kvantitet II: f(2)
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Vi sätter in noll och två i funktionen:
Funktionsvärdena är lika stora, alltså är svaret C.
Svar: C, I är lika med II.
För en viss parallellogram gäller att vinkeln i ett av hörnen är 57°.
Kvantitet I: Vinkeln i ett av de andra hörnen i parallellogrammen
Kvantitet II: 124°
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Ett parallellogram är en rektangel som knuffats åt sidan. Det betyder att motstående vinklar alltid är lika stora, men inte nödvändigtvis nittio grader. Eftersom vinkelsumman i alla fyrhörningar är 360 grader, kan de andra två vinklarna, v, beräknas:
Kvantitet II var 124 grader, och är alltså större än alla vinklar i parallellogrammen. Då kan vi sluta oss till att II är större än I.
Svar: B, II är större än I.
Tillägg: 19 mar 2022 19:12
Tillägg: Det finns tre andra vinklar i vårt parallellogram. De är 57, 123 och 123 grader stora. Kvantiteten 124 grader är större än alla tre. Om någon vinkel hade varit större än eller lika med 124 grader, hade vi inte kunnat dra någon slutsats. :)
Kvantitet I:
Kvantitet II:
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Här är det svårt att hitta något bra räknetips, men genom att använda parenteser kan man spara lite tid åtminstone:
Svar: A, I är större än II.
Alternativ metod från pelleplums: Använd konjugatregeln! Då fås att:
respektive
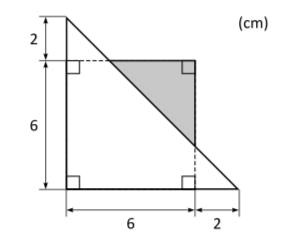 Kvantitet I: Arean av den skuggade ytan
Kvantitet I: Arean av den skuggade ytan
Kvantitet II:
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Eftersom triangeln är likbent, är de streckade linjerna också 2 cm långa. Därför måste den skuggade triangelns sidor vara cm långa, och arean av det skuggade området måste då vara . Då vet vi att den första kvantiteten är större än den andra.
Svar: A, I är större än II.
Medelvärdet av åtta på varandra följande heltal är 16,5.
Kvantitet I: Hälften av det största av de åtta heltalen
Kvantitet II: Det minsta av de åtta heltalen
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
På varandra följande heltal är tal som 1, 2, 3 eller 6, 7, 8, 9. Genom att kalla det fjärde talet för a, kan vi lätt summera dessa tal, och ta fram en ekvation med hjälp av medelvärdet. Eftersom talen följer på varandra ger detta talserien:
Summan av dessa tal är . Eftersom det är åtta tal, måste medelvärdet av talen vara (eftersom medelvärdet enligt uppgiften är 16,5). Detta ger oss att a = 16, och att talserien därmed går från 13 till 20. Hälften av det största talen är 10, vilket är mindre än 13, det minsta av talen. Alltså är svaret B, II är större än I.
Svar: B, II är större än I.
a>0
b>0
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Det finns skäl att misstänka att det är värt att utveckla Kvantitet I. Dessa typer av uttryck är nästintill omöjliga att värdera annars. Vi provar:
Genom att bryta ut ab från de två mittentermerna fås uttrycket . Med andra ord är kvantiteterna identiska.
Svar: C, I är lika med II.
x > 0
Kvantitet I:
Kvantitet II: x
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Genom att dra roten ur båda led fås att . Eftersom x enligt uppgiften ska vara större än 0, måste x = 0,5. Kvantitet I, , är lika med . Alltså är kvantitet II större än I.
Svar: B, II är större än I.
s är summan av alla heltal x sådana att 0 < x < 6.
p är produkten av alla primtal y sådana att 2 < y < 7.
Kvantitet I: s
Kvantitet II: p
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Kvantitet I: Summan av talen som uppfyller detta villkor är s = .
Kvantitet II: De enda primtal mellan två och sju är tre och fem. Produkten av dessa fås genom att multiplicera talen, vilket ger att p = 15.
Svar: C, I är lika med II.
En låda innehåller enfärgade klossar: röda, gröna och blå. Hur många klossar finns det
i lådan?
(1) Lådan innehåller 55 röda klossar, vilket är 10 procent mer än antalet gröna klossar.
(2) De blå och de gröna klossarna är sammanlagt lika många som de röda klossarna.
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
(1): Detta villkor säger ingenting om de blå klossarna, och räcker därför inte.
(2): Detta villkor ger endast information om hur förhållandet mellan klossarna ser ut. Vi hade behövt någon mer information om antal för att kunna lösa frågan.
Tillsammans: Vi vet hur många de röda klossarna är, och att de blå och gröna klossarna tillsammans är lika många. Vi kan lösa frågan.
Svar: C, i (1) tillsammans med (2).
Christian, Harry och Sam är tre bröder vars sammanlagda ålder är 16 år. Hur gammal är Sam?
(1) Christian och Harry är lika gamla.
(2) Sam är två år yngre än Harry.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Detta påstående säger ingenting om hur gammal Sam är. Summan av åldrarna är 16 år, men om Christian och Harry är ett år skulle Sam vara 14 år, medan Sam skulle vara åtta år gammal om Christian och Harry vore fyra år gamla. Detta räcker inte.
(2): Detta påstående säger ingenting om Christians ålder, och räcker därför inte heller.
Tillsammans: Vi har information om hur gamla alla tre personer är i förhållande till varandra, och med vetskapen om att summan av deras åldrar är 16 år, kan vi lösa uppgiften.
Svar: C, i (1) tillsammans med (2).
Då ett kafé öppnade fanns det en korg med röda äpplen och gröna äpplen. Sammanlagt fanns det 48 äpplen i korgen. Hur stor andel röda äpplen fanns det i korgen då kaféet öppnade?
(1) Då kaféet stängde fanns det tre röda och nio gröna äpplen kvar i korgen.
(2) Då kaféet öppnade fanns det tre gånger så många röda som gröna äpplen i korgen.
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
(1): Hur många äpplen det fanns vid stängningsdags säger oss ingenting, om vi inte samtidigt fått någon information om hur många äpplen som gått åt. Detta räcker inte.
(2): Vi vill veta hur stor andel röda äpplen det fanns i korgen. Här får vi att det är tre gånger fler röda äpplen än gröna. Det innebär att vi kan uttrycka andelen röda äpplen. Denna information är tillräcklig.
Svar: B, i (2) men ej i (1).
Alma och Karin går i samma skola. En morgon går Alma hemifrån klockan 8.02 och Karin går hemifrån klockan 8.05. Vem av dem kommer fram till skolan först?
(1) Alma och Karin har samma medelhastighet.
(2) Alma har 500 meter att gå till skolan och är framme klockan 8.10.
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
Här är det lätt att bli lurad av mängden information vi fått. Försök att hitta flera, olika möjliga fall.
(1): Att de har samma medelhastighet säger oss ingenting, utan att veta hur långt de måste gå. Detta räcker inte.
(2): Detta ger oss information om Almas hastighet, men utan någon vetskap om Karins sträcka till skolan ger detta oss ingenting. Detta räcker inte.
Tillsammans: Vi har fortfarande ingen information om Karins sträcka. Även om vi indirekt fått Karins hastighet via (1), vet vi fortfarande inte hur långt hon måste gå. Karin kan ha fem meter eller två mil till skolan, utan att veta något om Karins sträcka, eller tid i förhållande till Karin, kan vi inte säga något.
Svar: E, ej genom de båda påståendena.
Vilket värde har det positiva heltalet x?
(1) Om talen 63, 64 respektive 65 delas med x blir resten 15, 0 respektive 1.
(2) x är ett jämnt tal som är jämnt delbart med 4.
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
(1):
- Eftersom resten är noll då 64 divideras med x, måste x vara en faktor i 64. Bekvämt nog är 64 en potens av två, och kan skrivas . Det innebär att 2, 4, 8, 16, 32 och 64 är möjliga alternativ på x.
- När 63 divideras med x ska resten bli femton. Detta är användbart, eftersom x då måste vara större än femton. Detta går att visa matematiskt, men det är gott nog att tänka att om två hade varit faktorn, hade resten aldrig kunnat bli femton, utan hade varit antingen noll eller ett. Detsamma gäller för alla tal mindre än femton. Alltså kvarstår 16, 32 och 64.
- Eftersom resten är femton kan x inte vara 64, eftersom resten då 63 divideras med 64 är hela talet, 63. Kvar är då 16 och 32. Vi kan också testa att dividera 63 med 32, och kan då konstatera att resten blir 31. Alltså kvarstår endast 16 som ett möjligt alternativ.
- För att vara på den säkra sidan kan vitesta att 16 fungerar ihop med 65. , vilket är den rest som uppgiften frågar efter.
Sammanfattningsvis, (1) fungerar ensamt.
(2): "x är ett jämnt tal som är jämnt delbart med fyra" - Några sådana finns det ju. 4, 8, 12, 16, hela fyrans gångertabell fungerar. Detta räcker inte.
Svar: A, i (1) men ej i (2).
På en uteservering är det 10 gäster som har både solglasögon och keps, och 20 gäster som varken har solglasögon eller keps. Hur många gäster är det på uteserveringen?
(1) 15 gäster har solglasögon och 15 gäster har keps.
(2) 5 gäster har solglasögon men inte keps, och 5 gäster har keps men inte solglasögon.
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
Här är det läge att tänka Venndiagram! Vi ritar ett med informationen vi fått från uppgiften:
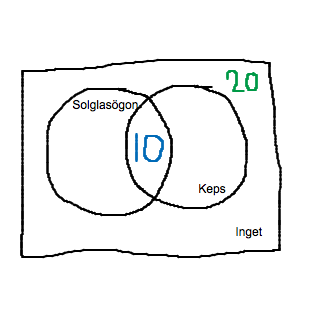
(1): Om vi vet att femton gäster har solglasögon, och att femton gäster har keps, kan vi fylla i alla fält, och därmed beräkna antalet gäster. Denna information duger.
(2): Även här vet vi hur många gäster som har bara keps, bara solglasögon, både och, respektive ingendera. Vi kan då beräkna antalet gäster.
Svar: D, i (1) och (2) var för sig.
Uppgift 29 - 31:
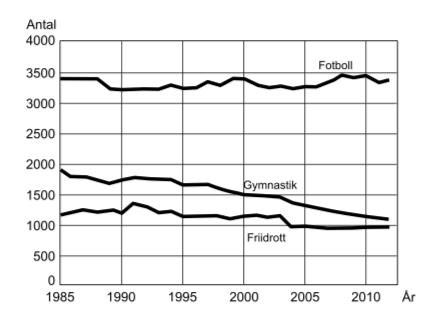
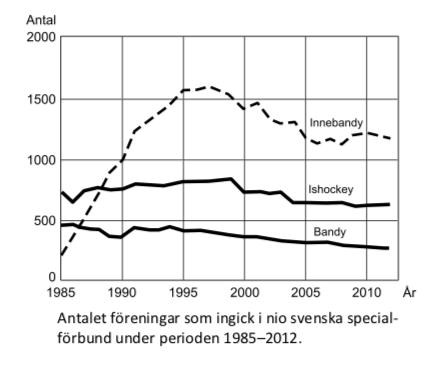
29. Hur stor var den procentuella minskningen av antalet gymnastikföreningar 2012 om man jämför med antalet 1985?
A: 40 procent
B: 50 procent
C: 60 procent
D: 70 procent
Markera det relevanta årtalet, och läs av storleken på y-axeln:
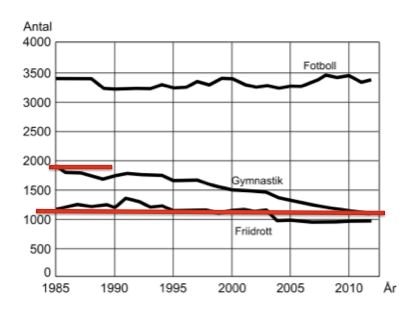
Antalet gymnastikföreningar har minskat från ungefär 1900 till 1100. Det är en minskning med 800 klubbar. I andelar är det .
Svar: A, 40 procent.
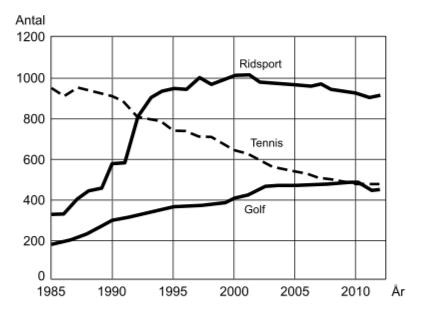
Hur många ridsportföreningar fanns det i genomsnitt per år under perioden 1990–2000?
A: 750
B: 850
C: 950
D: 1 050
Det går att räkna antalet klubbar under perioden, och dividera detta antal med tio år, men en snabbare metod är att markera svarsalternativen i diagrammet, och notera vilken linje som ser ut att passa bäst:
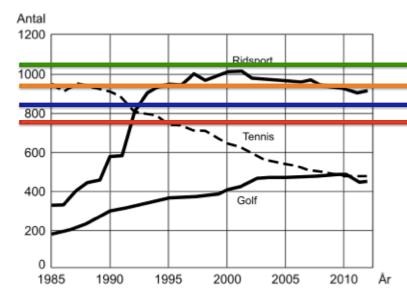
Den röda linjen, 750, ligger alldeles för lågt. Den gröna (1050) och den orangea (950) linjen ligger alldeles för högt, de kan inte vara medelvärdet ligger. Kvar är då endast 850 klubbar/år.
Svar: B, 850.
Studera hur antalet fotbollsföreningar och antalet friidrottsföreningar förhöll sig till varandra år 2000. Vilket svarsförslag anger storleksförhållandet mellan fotboll och friidrott?
A: 2:1
B: 3:1
C: 3:2
D: 5:2
Markera årtalet i diagrammet, och läs av antalen på y-axeln:
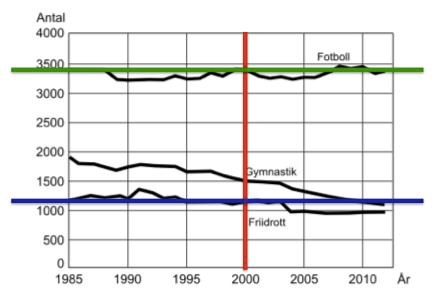
Fotboll tycks ha ungefär 3400 klubbar, medan friidrott verkar ha runt 1100 klubbar. Förhållandet är alltså 3400 : 1100, vilket kan förenklas ned direkt till 34 : 11. Genom att notera att , och att 34 ≈ 33, kan vi avrunda förhållandet till 33 : 11, alltså 3 : 1.
Svar: B, 3 : 1.
Uppgift 32 - 34:
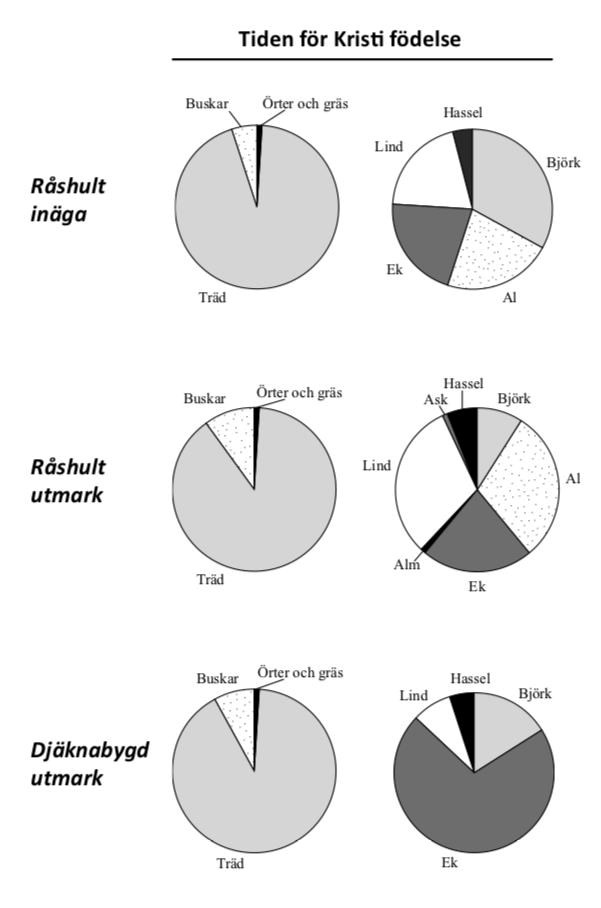
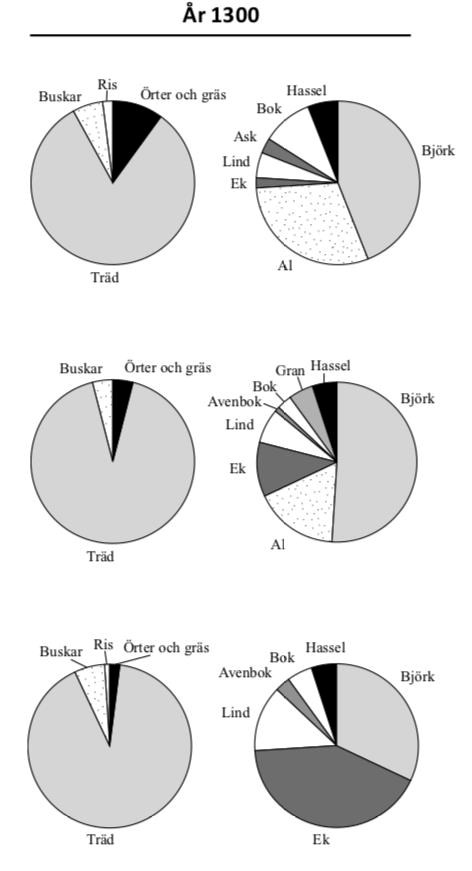
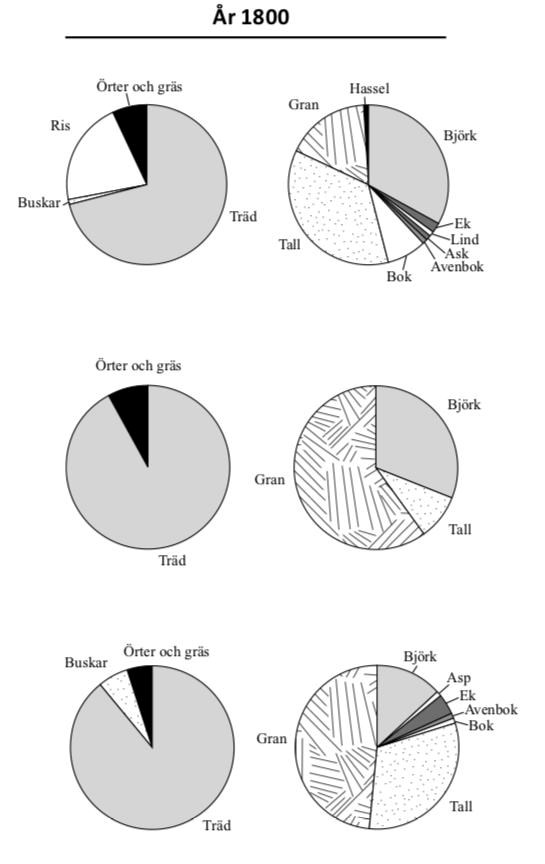
32: Vilket trädslag var vanligast på Råshult utmark vid tiden för Kristi födelse, år 1300 respektive år 1800?
A: Björk, björk respektive tall
B: Ek, björk respektive gran
C: Ek, ek respektive gran
D: Lind, björk respektive gran
Markera de relevanta pajerna i diagrammet, och ringa in deras vanligaste trädsort:
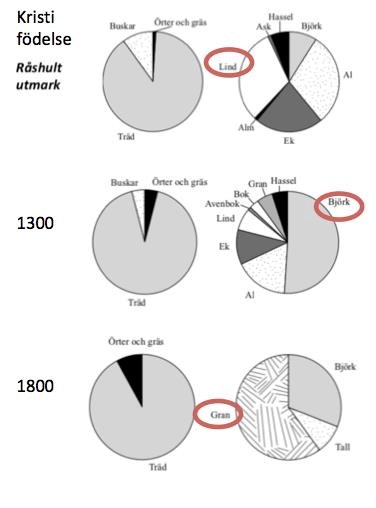
Vid Kristi födelse är det aningen oklart huruvida det är Al eller Lind som är vanligast, men eftersom de två sista alternativen ska vara "Björk, Gran", kan vi sluta oss till att det antingen är alternativ B eller D. Ek var verkligen inte det vanligaste trädet vid Kristi födelse, och alltså kan vi utesluta alternativ B också.
Svar: D, Lind, björk respektive gran.
33. På vilken av följande platser och vid vilken tidpunkt utgjorde örter och gräs 8 procent av vegetationen medan asp och al saknades?
A: Råshult inäga, år 1300
B: Djäknabygd utmark, år 1300
C: Råshult inäga, år 1800
D: Djäknabygd utmark, år 1800
Markera de relevanta pajerna, och stryk alla som har al och/eller asp:
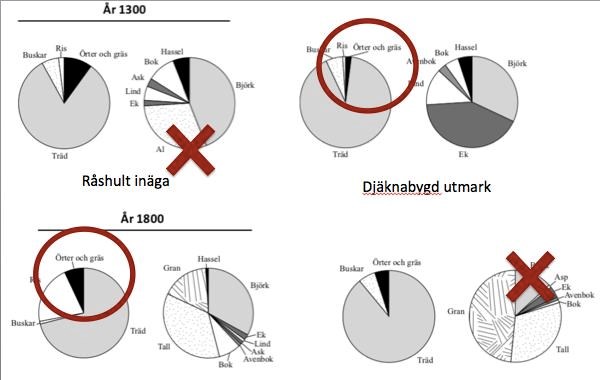
Eftersom Djäknabygds utmark endast har en mycket tunn strimma örter och gräs vid år 1300, kan vi sluta oss till att det är alternativ C som är korrekt.
Svar: C, Råshult inäga år 1800.
34. Hur förändrades andelen al av träden på Råshult inäga om man jämför år 1300 med tiden för Kristi födelse?
A: Den ökade med 10 procentenheter.
B: Den ökade med 25 procentenheter.
C: Den minskade med 15 procentenheter.
D: Den minskade med 45 procentenheter.
Markera de relevanta pajerna:
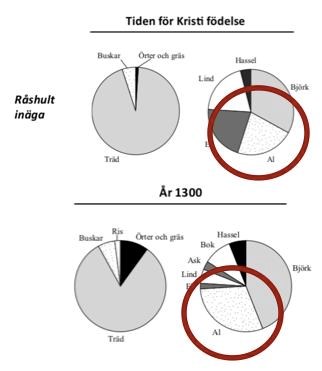
Det har helt klart skett en ökning. Då kan vi stryka alternativ C och D direkt. Vid Kristi födelse verkar det ha funnits ungefär 20% al, medan andelen tycks ha ökat till strax under 30% vid år 1300. Eftersom frågan frågar efter ökningen i procentenheter eftersöker vi skillnaden i procent, alltså 30% - 20% = 10%-enheter.
Svar: A, 10 procentenheter.
Uppgift 35 - 37:
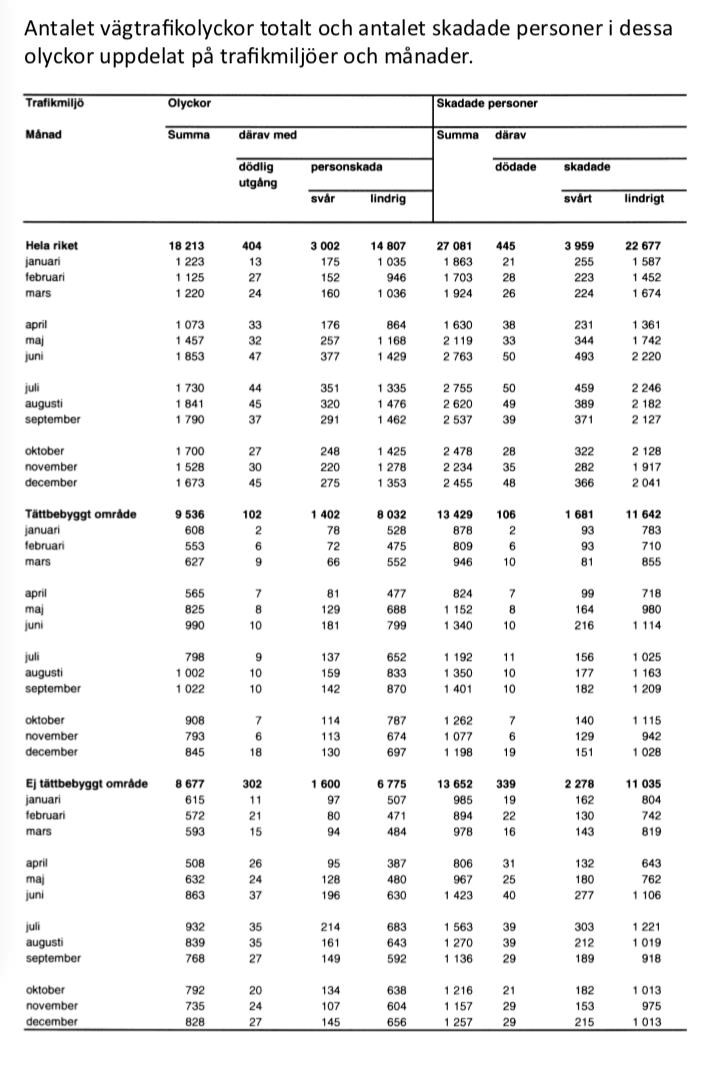
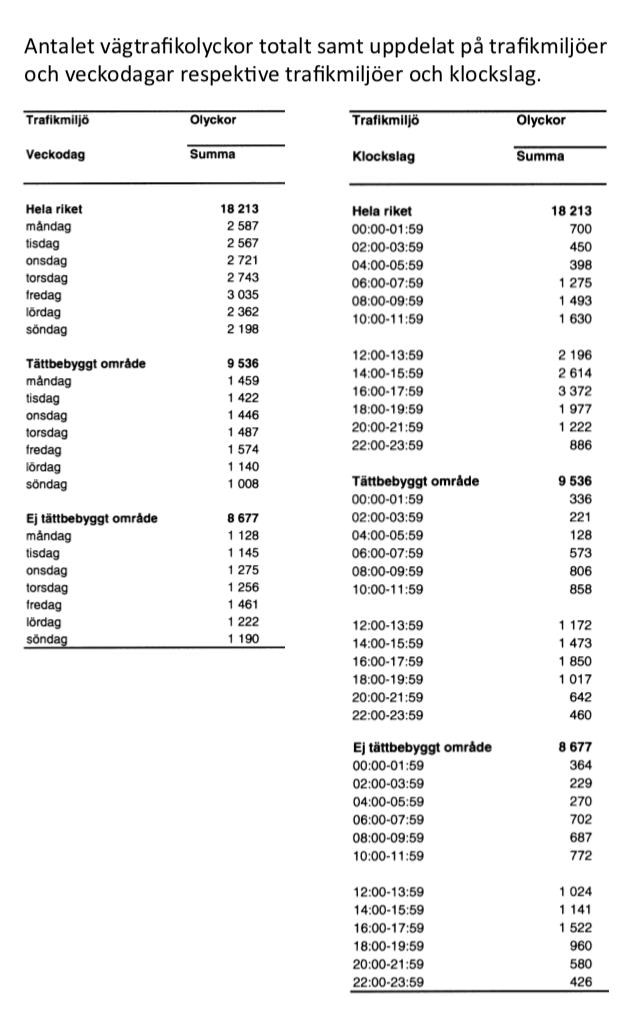
35. Vilken veckodag var antalet vägtrafikolyckor i ej tättbebyggt område som störst respektive som minst?
A: Onsdag respektive måndag
B: Onsdag respektive söndag
C: Fredag respektive måndag
D: Fredag respektive söndag
Identifiera det korrekta området, dvs. diagrammet över dagar, ej tättbebyggt område:

Vi kan läsa av att siffran är som högst för fredagar, och som lägst för måndagar.
Svar: C, Fredag respektive måndag.
36. Hur stor andel av vägtrafikolyckorna i tättbebyggt område skedde mellan 12.00 och 17.59?
A: 25 procent
B: 40 procent
C: 45 procent
D: 55 procent
Vi kikar i diagrammet över dagar och tid, och identifierar tidsintervallet:
 Vi gör en överslagsberäkning (två siffror avrundade uppåt och en nedåt, för att behålla symmetri) : olyckor. Totalt var antalet olyckor drygt 9500. Vi beräknar andelen:
Vi gör en överslagsberäkning (två siffror avrundade uppåt och en nedåt, för att behålla symmetri) : olyckor. Totalt var antalet olyckor drygt 9500. Vi beräknar andelen:
Svaret ska alltså vara ungefär 45%. Eftersom vi avrundat nämnaren uppåt, kommer svaret att vara aningen högre än 45%. Det gör att vi kan sluta oss till att svaret är 45% och inte 40%.
Svar: C, 45%
37. Nedanstående kurva visar hur antalet skadade personer i en viss kategori var fördelat på årets månader. Vilken kategori avses?
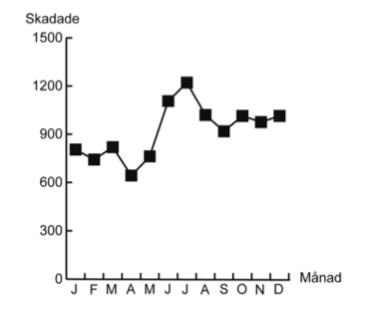 A: Det totala antalet skadade i tättbebyggt område
A: Det totala antalet skadade i tättbebyggt område
B: Antalet lindrigt skadade i tättbebyggt område
C: Det totala antalet skadade i ej tättbebyggt område
D: Antalet lindrigt skadade i ej tättbebyggt område
Vi identifierar de relevanta områdena i tabellen:
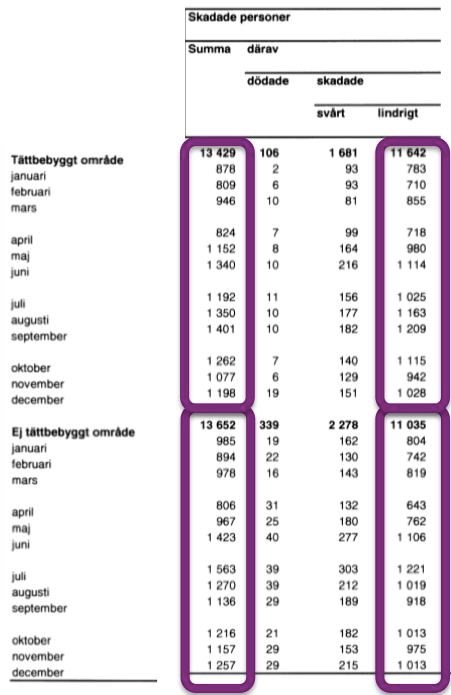
Sedan kan vi kika på juli månad, där värdet ska ligga mycket högt, över 1200 olyckor. Genom att läsa av värdena i tabellen för juli månad kan vi se att olycksstatistiken för de olika alternativen är:
A: 1192
B: 1025 (för lågt, uteslutet)
C: 1563 (för högt, uteslutet)
D: 1221
Vi har märkt att värdet ska ligga strax över 1200 personer, men för att vara på den säkra sidan kan vi även kika på värdena för juni och augusti. Dessa värden ska vara lägre än värdena för juli, vilket är korrekt för alternativ D, men inte för alternativ A. Då kan vi säkert sluta oss till att alternativ D är det korrekta.
Svar: D, Antalet lindrigt skadade i ej tättbebyggt område.
Uppgift 38 - 40:
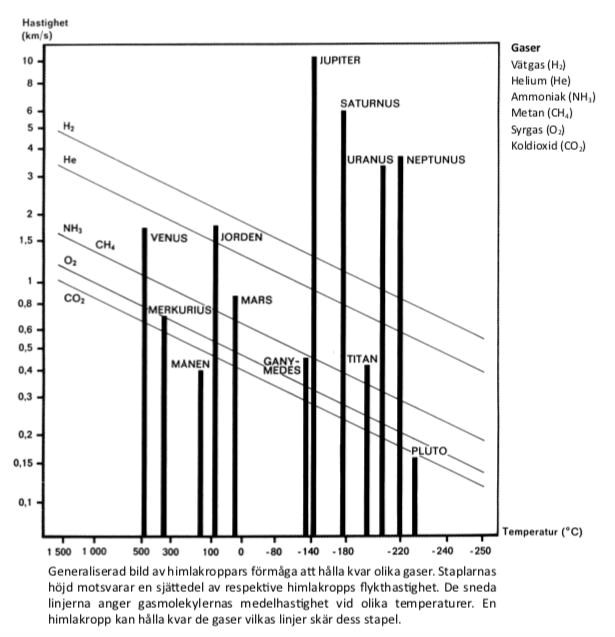
38. Jämför himlakroppen med den högsta redovisade temperaturen och himlakroppen
med den lägsta redovisade temperaturen. Hur stor är skillnaden?
A: 150°C
B: 250°C
C: 600°C
D: 700°C
De planeter med störst temperaturskillnad är Pluto och Venus:
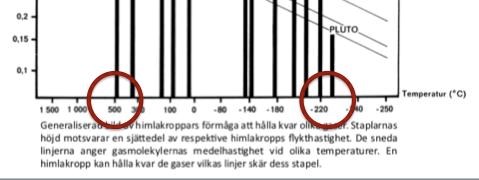
Venus är ganska precis 500 grader varm, medan temperaturen på Pluto är drygt -230 grader. Skillnaden här kan beräknas som (grader). Det alternativ som ligger närmast är D, 700 grader.
Svar: D, 700 grader.
Vilken temperatur redovisas för jorden och vilken medelhastighet har syrgas respektive koldioxid vid denna temperatur, enligt diagrammet?
Vi kikar i på jordens temperatur i diagrammet:

Temperaturen är knappt 100 grader, vilket utesluter alternativ C och D. Koldioxidens hastighet verkar dessutom vara runt 0,45 km/s, och syrgasens hastighet drygt 0,55. Alternativ A passar då mycket bra, medan alternativ B passar synnerligen dåligt.
Svar: A.
Vilken flykthastighet har månen?
A: 0,6 km/s
B: 0,8 km/s
C: 1,2 km/s
D: 2,4 km/s
Här gäller det att läsa det finstilta, dvs. tabelltexten:
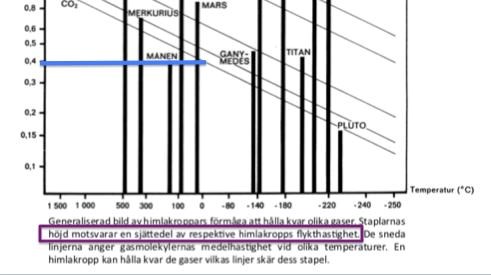
Höjden i diagrammet är en sjättedel av den verkliga hastigheten. Månens stapel är ungefär 0,4 km/s hög, vilket ger att flykthastigheten hos månen är (km/s). Detta passar utmärkt med alternativ D.
Svar: D, 2.4 km/s.
Vilket värde har x om ?
A:
B:
C:
D: 1
Eftersom alla x finns i täljarna, och det är jobbigt att räkna med bråk, kan vi multiplicera båda led med bråkens minsta gemensamma nämnare:
Svar: B, .
I en påse finns det 1 röd, 2 gröna, 3 blå, 4 vita och 5 svarta kulor. Om man drar en kula slumpmässigt, vad är då sannolikheten att den är antingen röd eller vit?
A:
B:
C:
D:
En kula kan inte vara röd och vit samtidigt. Vi behöver alltså inte räkna bort några överlappande fall. Sannolikheten, P, definieras som . Det totala antalet utfall är antalet kulor, alltså . Antalet gynnsamma utfall är antalet röda och vita kulor, alltså . Sannolikheten är då .
Svar: D,
Vilket svarsalternativ motsvarar linjen i figuren?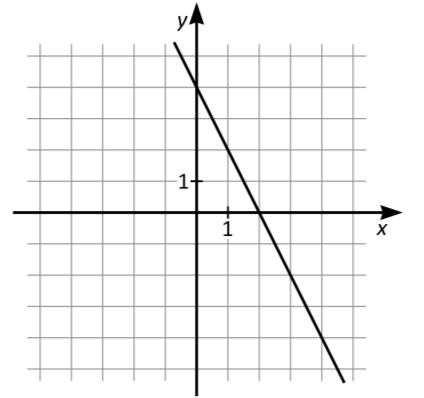 A:
A:
B:
C:
D:
Räta linjer kan skrivas på formen . m-värdet är värdet där linjen skär y-axeln, vilket i detta fall är då y = 4, vilket ger att D är rätt svar.
Svar: D,
Vilket av svarsalternativen motsvarar uttrycket ?
A:
B:
C:
D:
Multiplicera alla termer i den ena parentesen med alla termer i den andra. Detta är ofta lättast att göra visuellt:
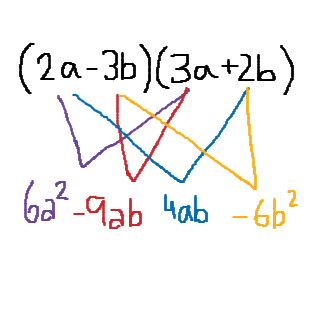
Förenkling av dessa termer ger att .
Svar: C, .
EDIT: En sexa hade försvunnit ur svaret, det är rättat nu.
Vilket värde har uttrycket?
A:
B:
C:
D:
Här är det lättast att omvandla till minsta gemensamma nämnare. 3, 9, 27, 81 är en serie av olika potenser av tre. . Omvandla av de andra nämnarna sker lätt genom att förlänga med lämpligt många treor:
Svar: B, .
En cirkel är placerad i ett koordinatsystem. AB är cirkelns diameter. Cirkelns medelpunkt har koordinaterna (−2, 1) och A har koordinaterna (−4, −2). Vad är koordinaterna för B?
A: (4, 0)
B: (0, 4)
C: (4, 2)
D: (2, 4)
Rita upp en ungefärlig bild!
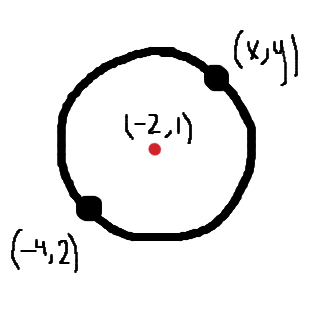
(Obs! Koordinaten i bilden ska heta (-4, -2), mitt misstag)
Avståndet i x- och y-led måste vara lika stort mellan den givna punkten och mitten, som mellan mitten och den motstående punkten. Avståndet i x-led mellan den givna punkten och mitten är 2 steg. Alltså är x-koordinaten för den motstående, sökta punkten, lika med noll. Då kan vi sluta oss till att alternativ B är det rätta.
Svar: B, (0, 4)
är parallell med .
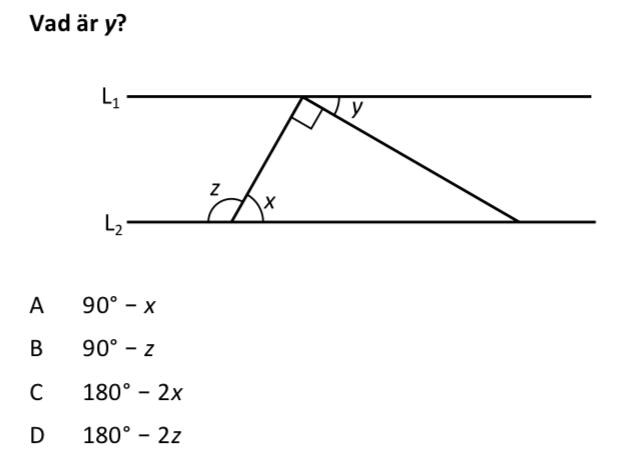
För två räta linjer som korsas av den tredje linje gäller följande:
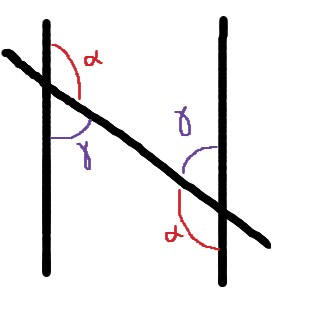
Det medför att vi kan konstatera att vinklarna inuti triangeln i bilden är 90 grader, x samt y. Deras vinkelsumma ska vara 180 grader, eftersom det är en triangel. Det ger summan:
Genom att subtrahera 90 från båda led fås:
Eftersom vi söker värdet på y, kan vi subtrahera x från båda led och få ut att , vilket motsvarar alternativ A.
Svar: A, .
Vad är x?
A: 1,5
B: 2
C: 2,5
D: 3
Vi kan multiplicera ihop parentesen i högerledet, och får då:
Genom att subtrahera från båda led fås ekvationen:
Subtrahera 6x och 7 från båda led:
Svar: C, 2.5.
En cirkel är placerad på den likbenta triangeln ABC så att cirkelns medelpunkt ligger mitt på hypotenusan AC och cirkeln tangerar kateterna AB och BC. Arean av triangeln är 50 cm2. Vad är omkretsen av cirkeln?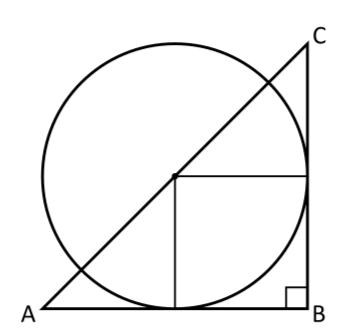
A: cm
B: cm
C: cm
D: cm
En cirkels omkrets, . Om vi kan hitta längden av triangelns kateter, kan vi hitta cirkelns omkrets. Vi har fått veta att triangeln är likbent, alltså att AB och BC är lika långa, samt att arean är 50 cm2. Med hjälp av formeln för triangelns area, , samt att b = h, kan vi få ut att (vi förkastar den negativa lösningen eftersom en sträcka inte kan vara negativ).
Eftersom cirkelns medelpunkt ligger på mitten av hypotenusan, och cirkeln precis tangerar triangelns kateter, måste cirkeln dela triangelns sidor i två. De två radier som är utmärkta i figuren måste alltså vara cm långa. Då är cirkelns omkrets lika med .
Svar: A, .
x och y är positiva tvåsiffriga heltal med samma siffror, men de två talen har siffrorna i omvänd ordning. Vilket tal är x + y med säkerhet jämnt delbart med?
A: 2
B: 3
C: 5
D: 11
Här är det lättaste att ta två tal som uppfyller kraven, exempelvis 12 och 21. Deras summa är 33, som är delbar med tre och elva. För att sluta oss till om det tre eller elva som är rätt svar, kan vi ta ett till exempel, såsom 14 och 41. Deras produkt är 55, vilket är delbart med fem och elva. Vi har nu endast ett tal som kan stämma med beskrivningen, elva, och det får bli vårt svar.
Svar: D, 11.
Vilket av svarsalternativen är inte ett möjligt värde på x om ?
A: 0
B: 1
C: −1
D: −2
Det går att lösa denna ekvation algebraiskt, men det är krångligt och det finns det inte tid till. Det är lättare att bara sätta in och prova. Noll kan vi utesluta direkt, eftersom vänsterledet blir noll. Vi undersöker vad som händer om x = 1:
x = 1 är ett möjligt värde på x, och vi kan därför utesluta svarsalternativ B. Vad händer om x = (-1)?
x = -1 är inte ett möjligt värde på x, och vi har vårt svar!
Svar: C, -1.
Vad är ?
A:
B: 1
C:
D: 3
Detta tal ser väldigt jobbigt ut, men är egentligen inte så farligt. Vi börjar med exponenten, och konstaterar att . Vårt uttryck är nu , vilket är samma sak som .
Svar: D, 3.
Kvantitet I: x
Kvantitet II: 0
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Vi löser ekvationen:
Kvantitet I är lika med kvantitet II, alltså måste svaret vara C.
Svar: C, I är lika med II.
Kvantitet I:
Kvantitet II: 10
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Roten ur fjorton är ett tal som är svårt att räkna ut, men eftersom , måste vara mindre än fyra. Roten ur 36 är lika med sex. Eftersom roten ur fjorton är mindre än fyra, måste summan vara mindre än tio.
Svar: B, II är större än I.
Kvantitet I: Avståndet mellan punkterna (1, 2) och (2, 4)
Kvantitet II: Avståndet mellan punkterna (1, 2) och (2, -4)
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Det går att använda Pythagoras sats för att hitta avstånd mellan två punkter, men i detta fall går det fortare att bara jämföra avstånden. Avståenden går från samma punkt, till punkter med samma x-koordinat. Därför är y-koordinaterna det enda som kommer att avgöra storleken på avståndet. Avståndet mellan 2 och 4 är mindre än avståndet mellan 2 och -4. Därför måste avståndet i kvantitet II vara större än avståndet i kvantitet I.
Svar: B, II är större än I.
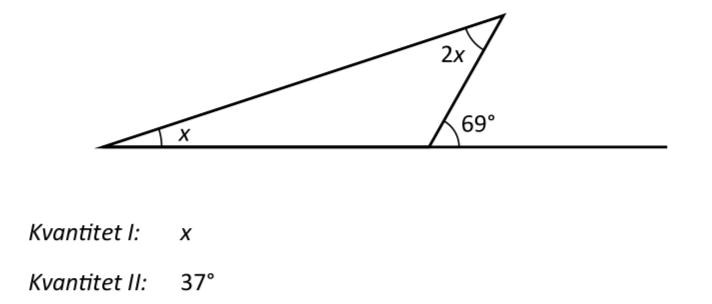
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Den som minns yttervinkelsatsen kan med fördel använda den, annars går det bra att använda sig av att räta linjer och trianglar har vinkelsumman 180 grader. Den omärkta vinkeln kan, med hjälp av triangelns vinkelsumma, beräknas till 111 grader. Det innebär att de två övriga vinklarna i triangeln måste dela på 180 - 111 grader, alltså 69 grader (yttervinkelsatsen):
En jämförelse med kvantitet II ger att II är större än I.
Svar: B, II är större än I.
Mätserie x: 15, 13, 20
Mätserie y: 30, 15, 11, 13
Kvantitet I: Medianen i mätserie x
Kvantitet II: Medianen i mätserie y
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Medianen är det mittersta av talen i en talserie, när de står i storleksordning. Medianen är mätserie x är 15. I mätserie y har vi inget mittersta tal. Då måste vi beräkna medelvärdet av de två mittersta talen, 13 och 15. Detta medelvärde kan beräknas till 14, alternativt går det att direkt dra slutsatsen att medelvärdet måste vara mindre än det största talet, och därmed mindre än 15.
Svar: A, I är större än II.
, där n är ett positivt heltal.
Kvantitet I: Entalssiffran i talet x
Kvantitet II: 4
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Eftersom vi inte vet någonting om n, är det här rimligt att misstänka att informationen är otillräcklig. Vi letar därför flera fall. Entalssiffran i tal som är potenser av fyra kan endast vara några få siffror:
Vi har nu två olika kvantiteter, och beroende på vilken av dem vi väljer, kommer storleksförhållandet mellan I och II vara olika. Därmed räcker inte vår information.
Svar: D, informationen är otillräcklig.
ABCD är en rektangel, och cirkelbågarna AB och CD är halvcirklar.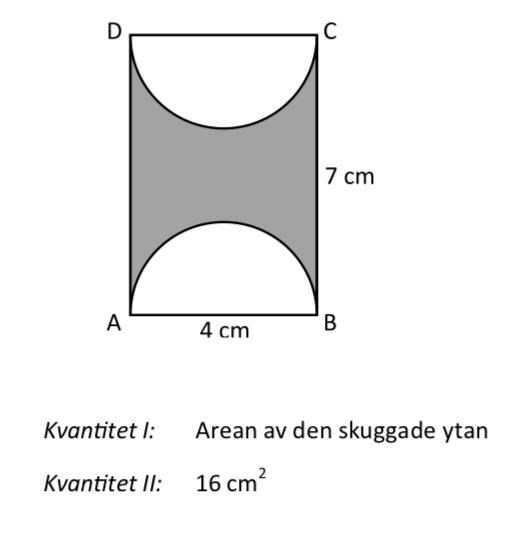 A: I är större än II
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
De två halvcirklarna är lika stora, och kan därför räknas ihop till en cirkel med radien två centimeter. Cirkelns area ges som , vilket med r = 2, ger att . Hela rektangelns area är . Det skuggade områdets area måste då vara . Frågan är nu om det området är större än eller mindre än 16 kvadratcentimeter. Vi vet att pi är större än 3, ungefär 3,14. Då måste vara större än 12. Det medför att måste vara mindre än 16. I är då mindre än II, och vi har vårt svar.
Svar: B, II är större än I.
x>y
y< 0
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Detta är ännu en sådan uppgift där man kan börja ana att det saknas tillräcklig information. Vi försöker därför hitta fall som går emot varandra:
Om x = 5 och y = -7, är x2 = 25, och y2 = 49, alltså II > I. Om däremot x = 5 och y = -2, fortfarande en tillåten kombination, är x2 = 25 och y2 = 4. Vi har två motstridiga fall, och därmed kan vi konstatera att det saknas tillräcklig information.
Svar: D, informationen är otillräcklig.
Det tar 30 minuter för 14 likadana pumpar att tillsammans fylla en tank med .
vatten.
Kvantitet I: Den tid det tar för 42 likadana pumpar att tillsammans fylla en tank med vatten
Kvantitet II: 1,5 timmar
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Här är det värt att notera att . Om fjorton pumpar fyller en tank med sju kubikmeter vatten på en halvtimme, kan 42 kranar åstadkomma totalt liter vatten på en halvtimme. Eftersom , kan vi konstatera att det kommer att ta tre halvtimmar att fylla tanken med 63 kubikmeter vatten. Tre halvtimmar är samma sak som 1,5 timmar, och därmed är I = II.
Svar: C, I är lika med II.
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: informationen är otillräcklig
Här gäller det att hålla tungan i mun. Vi kan skriva som . Men det är samma sak som . Eftersom x är större än noll, är 4x större än 2x, och därmed kan vi dra slutsatsen att I är större än II.
Svar: A, I är större än II.
I en låda fanns det ett antal kulor. Vid ett tillfälle läggs 42 nya kulor ner i lådan.
Hur många kulor finns det i lådan när de 42 nya kulorna har lagts ner?
(1) Innan de 42 nya kulorna lades ner var antalet kulor i lådan 28 % mindre än efteråt.
(2) De 42 nya kulorna utgör 7/25 av alla kulor i lådan.
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
När det kommer till antal och procent behöver vi två av tre informationsbitar: Andelen/procentsatsen, delen, det hela antalet. Har vi två av dessa, kan vi beräkna den tredje.
(1) Här har vi fått uppgift om en procentsats och en del, om kulorna innan ökningen. Detta duger för att beräkna antalet kulor efter ökningen.
(2) Här har vi fått uppgifter om en del och en andel, det duger för att beräkna svaret.
Svar: D, i (1) och (2) var för sig.
Medelvärdet av tre tal är 19. Vad är talens median?
(1) Ett av talen är 14.
(2) Ett av talen är 27.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
Det mittersta talet är medianen, som vi letar efter. Om vi vet två av de tre tal som ingår i medelvärdet, samt medelvärdet, kan vi beräkna det tredje.
(1) Här vet vi endast om ett tal, utöver medelvärdet. Det räcker inte.
(2) Precis som i (1). Här vet vi endast om ett tal, utöver medelvärdet. Det räcker inte.
Tillsammans: Här har vi fått två av tre tal, samt medelvärdet. Då kan vi beräkna det tredje talet, och därifrån ta fram medianen. Detta räcker.
Svar: C, i (1) och (2) tillsammans.
I ett pennställ finns det endast enfärgade pennor: 12 röda och 16 blå. Hur många av pennorna i pennstället är trasiga?
(1) En tredjedel av de röda pennorna är trasiga.
(2) Om en trasig röd penna plockas upp ur pennstället så finns det tre gånger så många trasiga blå pennor som trasiga röda pennor kvar i pennstället.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
Här har vi fyra olika bitar av information: Antalet röda pennor, antalet trasiga röda pennor, antalet blåa pennor och antalet trasiga blåa pennor. Vi har fått information om det totala antalet pennor av varje färg. Nu behöver vi endast information om antalet trasiga pennor av varje färg:
(1) Detta säger ingenting om antalet trasiga blåa pennor. Detta räcker inte.
(2) Detta låter bra, eftersom vi får information om förhållandet mellan antalet trasiga röda och blå pennor. Det är dock värt att undersöka om det kan finnas flera olika fall. Om det finns fem trasiga röda pennor, måste det finnas tolv trasiga blåa pennor. Det skulle kunna stämma med det totala antalet pennor. Om det finns fyra trasiga röda pennor, måste det finnas nio trasiga blåa pennor, vilket också skulle kunna fungera. Vi har två olika fall, och därför räcker inte denna information.
Tillsammans: Med hjälp av (1) kan vi beräkna hur många av de röda pennorna som är trasiga, samt hur de trasiga röda pennorna förhåller sig till de trasiga blåa pennorna. Vi kan beräkna antalet trasiga blåa pennor med hjälp av denna information, och då har vi alla fyra bitar information.
Svar: C, i (1) tillsammans med (2).
Anna, David, Frida och Johan är syskon. Vem av syskonen är yngst?
(1) Anna är äldre än Frida. Frida är yngre än David.
(2) David är äldre än Johan. Johan är yngre än Anna.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
Vi har fyra personer vi behöver information om.
(1) Vi kan ställa upp att . Detta säger dock ingenting om Johans ålder.
(2) Vi kan ställa upp att , men detta säger oss ingenting om Fridas ålder.
Tillsammans: Vi kan sortera att och att , men utan någon information om hur Frida och Johan förhåller sig i ålder, finns det ingenting vi kan göra här.
Svar: E, ej genom de båda påståendena.
Kalle har 15 enfärgade kulor i sin ficka. Kulorna har tre olika färger. Om Kalle slumpmässigt tar kulor ur fickan, vilket är då det minsta antal kulor som Kalle måste ta upp för att säkert få minst en kula av varje färg?
(1) 1/3 av antalet kulor är svarta.
(2) 7 kulor är röda och 3 kulor är blå.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
Vi behöver veta hur många kulor det finns av varje färg, tre stycken, samt det totala antalet. Detta är fyra bitar information, och om vi vet tre av dessa kan vi ta fram den fjärde. Vi har redan fått en bit, det totala antalet.
(1): Detta ger oss en bit information, men vi saknar fortfarande två. De tio resterande kulorna kan vara 3 st. röda och 7 st. blå, eller vice versa, exempelvis. Detta är inte tillräckligt.
(2): Här får vi två bitar information, och med hjälp av dessa två bitar (samt den bit som getts i uppgiften), kan vi ta fram den sista biten information. Detta är tillräckligt.
Svar: B, i (2) men ej i (1).
ABC är en triangel. Punkten D ligger på BC. Sträckorna AC, AD och BD är 4 cm långa. Hur stor är vinkeln x?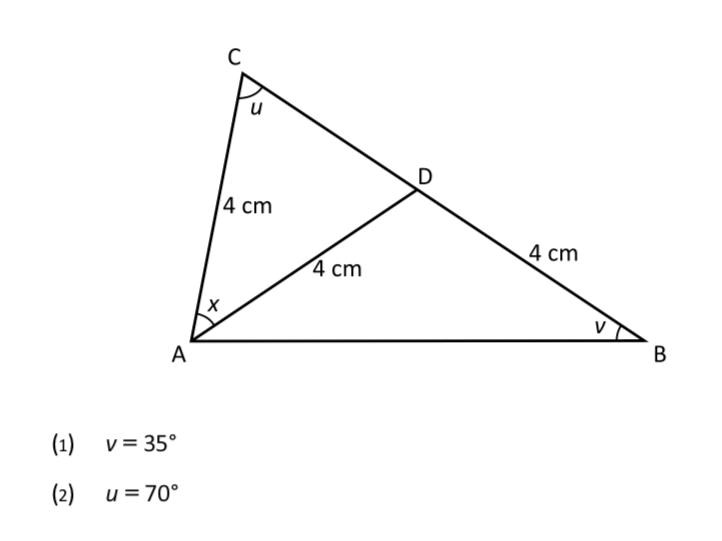
Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena
Genom att markera de sträckor som är lika långa, får vi fram att figurens två inre trianglar båda är likbenta. Det medför att vinkeln ADC är lika med u, och att vinkeln DAB är lika med v.
(1) Genom att vi fått vinkeln v kan vi beräkna vinkeln ADB. Då kan vi även beräkna vinkeln u, eftersom en rät linje alltid är 180 grader. Med hjälp av triangelns vinkelsumma kan vi då beräkna x. Detta räcker.
(2) Här får vi u, och kan med hjälp av triangelns vinkelsumma direkt beräkna x. Detta räcker.
Svar: D, i (1) och (2) var för sig.
Uppgift 29 - 31:
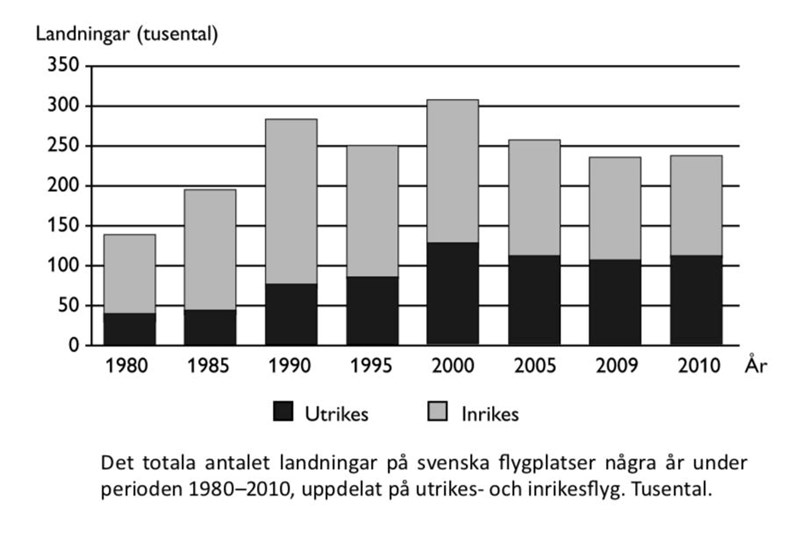
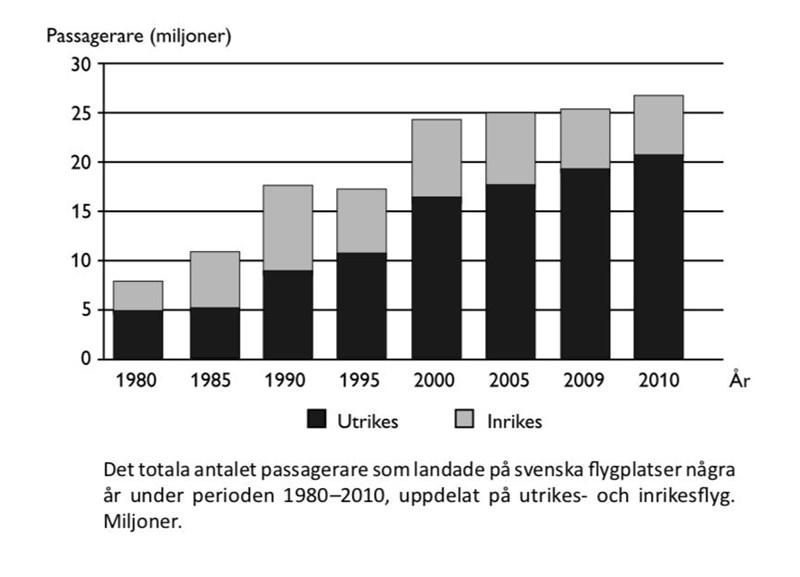
29. Hur stort var antalet passagerare per landning på svenska flygplatser 2005?
A: 50
B: 100
C: 150
D: 250
Läs av antalet passagerare och landningar:
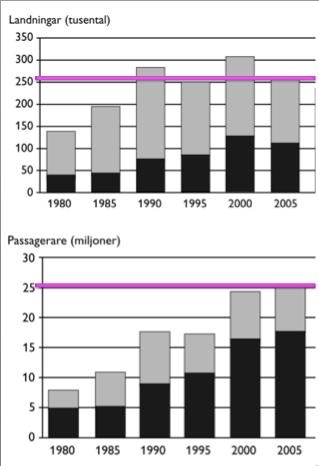
Drygt 250 000 landningar, och totalt ungefär 25 miljoner passagerare. Per landning blir det:
passagerare per landning.
Svar: B, 100.
30. Med hur många procent hade antalet utrikes passagerare ökat 2010 om man jämför med 1980?
A: 120 procent
B: 250 procent
C: 320 procent
D: 450 procent
Markera de relevanta årtalen i diagrammet, och läs av antalet passagerare:
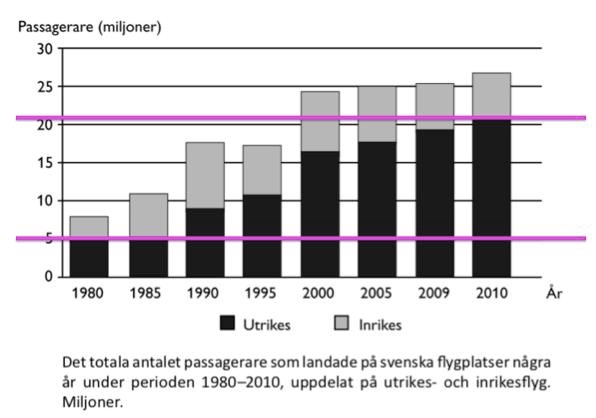
Vid 1980 var antalet utrikes passagerare drygt fem miljoner, och vid år 2010 var de strax över 20 miljoner. Detta ger en procentuell skillnad:
Eftersom det fanns 100% passagerare vid 1980, måste vi subtrahera 100% från vår nya procentsats, och får då att ökningen i procent är drygt 300%.
Svar: C, 320 procent.
31. Hur stor var skillnaden i antal landningar mellan inrikes- och utrikesflyg år 2000?
A: 50 000
B: 90 000
C: 125 000
D: 165 000
Markera det relevanta årtalet och dra ungefärliga linjer:
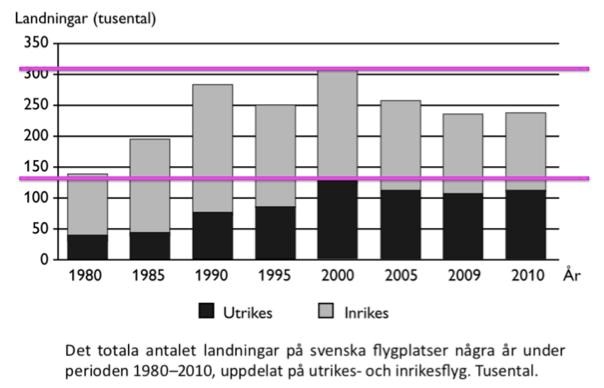
Antalet inrikes landningar var drygt landningar. Antalet utrikes landningar var 125 000, vilket ger att skillnaden mellan antalet inrikes och utrikes landningar är landningar.
Svar: A, 50 000.
Uppgift 32 - 34:
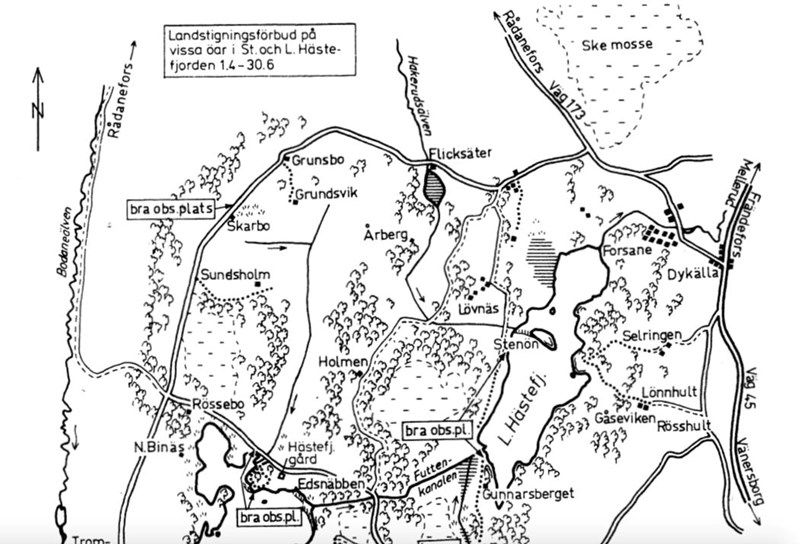
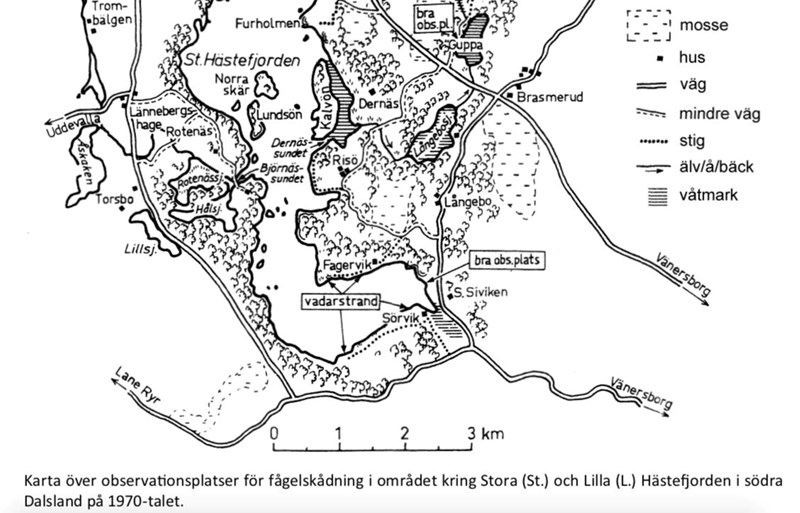
32. Var slutar följande vägbeskrivning?
Utgå från den fyrvägskorsning som ligger närmast Brasmerud och välj den väg som går i nordvästlig riktning. Ta efter drygt 3 kilometer av på en mindre väg som går i nordlig riktning och följ denna väg i 2 kilometer.
A: Holmen
B: Rössebo
C: Furholmen
D: Lönnhult
Markera fyrvägskorsningen vid Bramserud, och använd skalan för att markera 3 km längs vägen som går nordväst. Det leder till en liten avtagsväg som går norrut. Följ denna i två kilometer, så kommer du till Holmen:
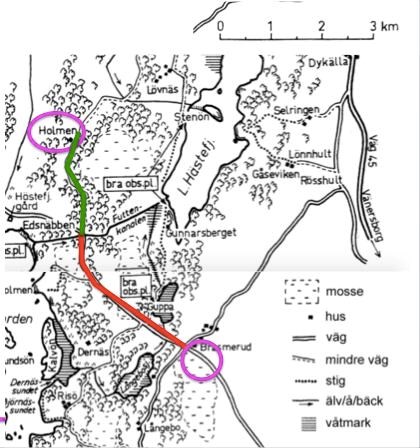
Svar: A, Holmen.
33. I vilken riktning rinner Hakerudsälven när den når fram till Lilla Hästefjorden?
A: Nordostlig riktning
B: Ostlig riktning
C: Sydostlig riktning
D: Sydlig riktning
Identifiera Hakerudsälven, den börjar längst upp på kartan, och följ denna älv. Rita en pil i älvens riktning när du når Lilla Hästefjorden.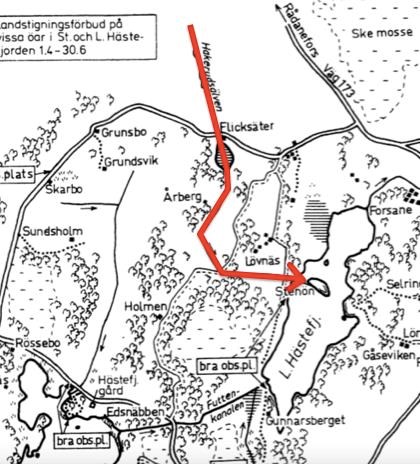
När älven når fjorden rinner den österut.
Svar: B, Ostlig riktning.
34. Du cykar från Grunsbo och ska besöka tre av de ”bra observationsplatser” som finns utmärkta på kartan. Platserna är den i Skarbo, den som ligger längst norrut i Stora Hästefjorden samt den vid S. Siviken. Platserna besöks i den nämnda ordningen. Du följer vägen förbi dessa platser, och efter sista stoppet vid observationsplatsen i S. Siviken tar du vägen via Torsbo tillbaka till Grunsbo. Du startar klockan 12.00, cyklar 20 km/h och stannar på varje observationsplats i en timme. Vilken tid kommer du tillbaka till Grunsbo?
A: Klockan 13.30
B: Klockan 14.30
C: Klockan 15.30
D: Klockan 16.30
Mät inte ihjäl dig här, utan börja med att titta på tiden du ska stanna på varje plats. Det är tre platser, och du stannar i en timme på varje. Då kan du direkt utesluta alternativ A och B. Genom att markera (åtminstone en del av) vägen, blir det tydligt hur lång vägen är:
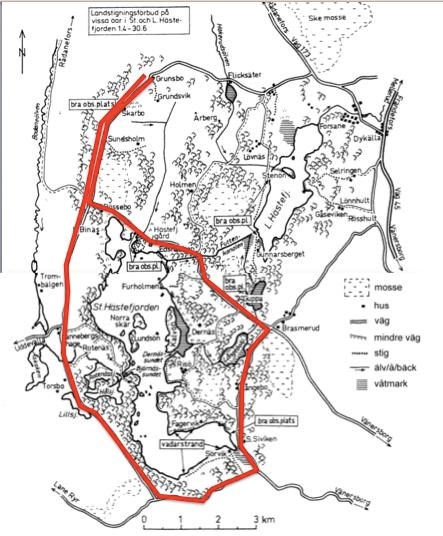
Det finns ingen chans att du kan cykla så långt på en halvtimme. Alltså är alternativ C, 15:30, också orimligt. Kvar finns då endast alternativ D.
Svar: D, Klockan 16:30.
Uppgift 35 - 37:
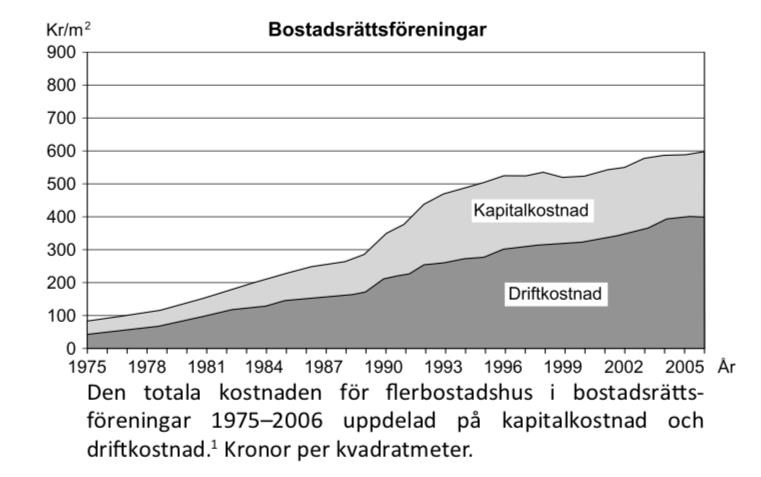
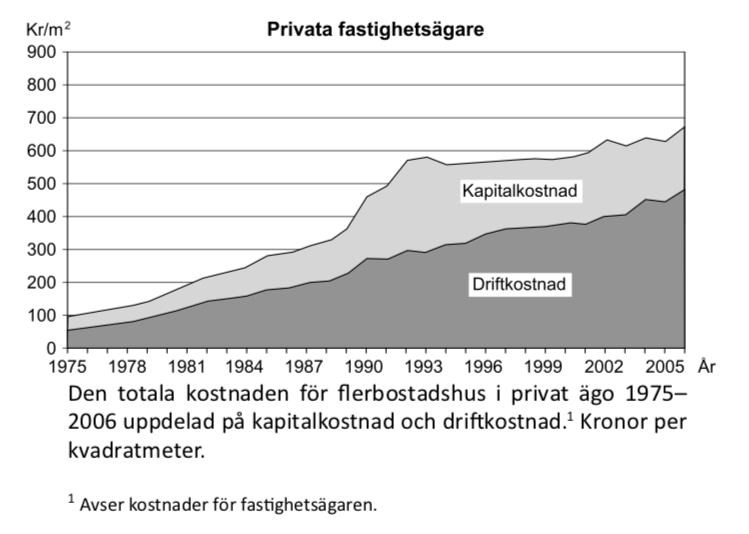
35. Jämför den totala kostnaden för flerbostadshus i allmännyttiga bostadsföretag och den totala kostnaden för flerbostadshus i bostadsrättsföreningar. Hur stor var skillnaden 2002?
A:
B:
C:
D:
Markera året, och läs av kostnaderna:
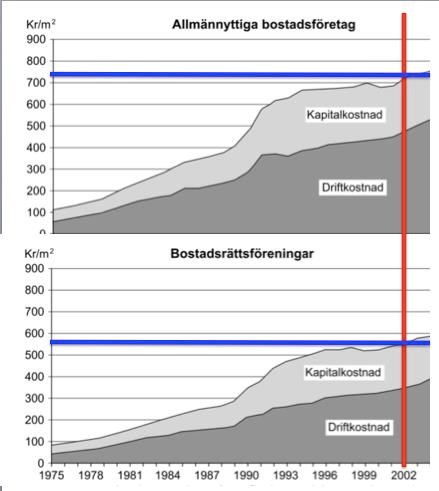
För allmännyttiga fastigheter var kostnaden drygt 730 kr/m2. För bostadsrättsföreningar var samma kostnad ungefär 570 kr/m2. Dessa siffror ger skillnaden i totalkostnad:
(kr/m2)
Det närmaste värdet är alternativ D, 175 kr/m2.
Svar: D, 175 kr/m2.
36. Hur stor andel av den totala kostnaden för allmännyttiga bostadsföretag 1975 respektive 2006 utgjordes av kapitalkostnad?
A: 30 procent respektive 25 procent
B: 40 procent respektive 35 procent
C: 50 procent respektive 25 procent
D: 60 procent respektive 35 procent
Ett lätt sätt att tappa tid på denna uppgift är att räkna ihjäl sig. Det är dumt. Markera årtal och kostnader i diagrammet:
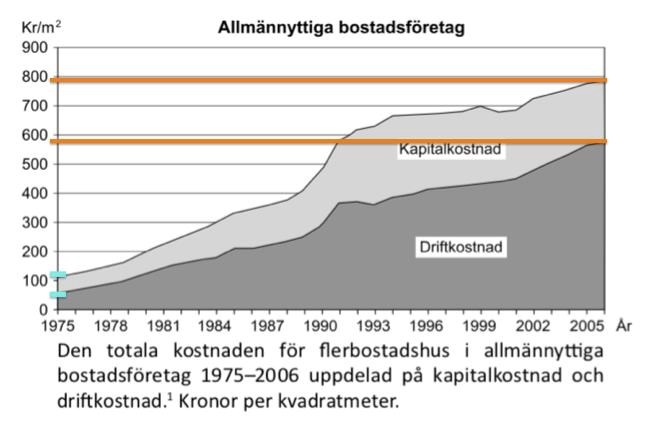
Vid 1975 (turkosa linjer) verkar kapitalkostnaden utgöra ungefär hälften av den totala kostnaden, alltså 50%. Redan här kan vi välja alternativ C. För att vara på den säkra sidan kan vi kika på hur det såg ut 2006. Då verkar kapitalkostnaden vara ungefär en fjärdedel av de totala kostnaderna. Detta stämmer väl med alternativ C:s svar, 25%, och då kan vi säkert sluta oss till att C är korrekt.
Svar: C, 50 procent respektive 25 procent.
EDIT: Bilden är utbytt, då jag av oklar anledning råkat läsa "1986" istället för 1975.
I nedanstående cirkeldiagram redovisas hur driftkostnaden för flerbostadshus i allmännyttiga bostadsföretag var fördelad på olika poster år 2000. Vilken typ av driftkostnad motsvarade 115 kronor per kvadratmeter?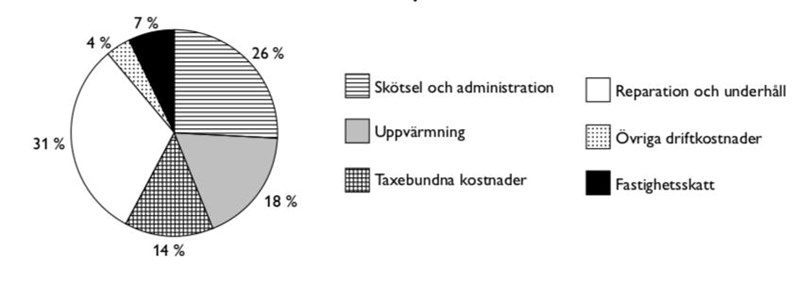 A: Skötsel och administration
A: Skötsel och administration
B: Uppvärmning
C: Taxebundna kostnader
D: Reparation och underhåll
Vi kan avläsa att driftkostnaderna för allmännyttiga flerbostadshus var drygt 450 kr/m2 år 2000. Vi vill hitta en procentsats hos de olika utgifterna, så att kostnaden för den utgiften blir 115 kr/m2. En fjärdedel (25%) av 400 är 100, vilket borde betyda att 25% av 450 är ungefär 110 kr/m2. Vi behöver därmed hitta någon utgift som är ungefär 25% stor, och då ligger Skötsel och administration, med sina 26%, nära till hands. De andra posterna är för stora eller för små för att kunna passa.
Svar: A, Skötsel och administration.
Uppgift 38 -40:
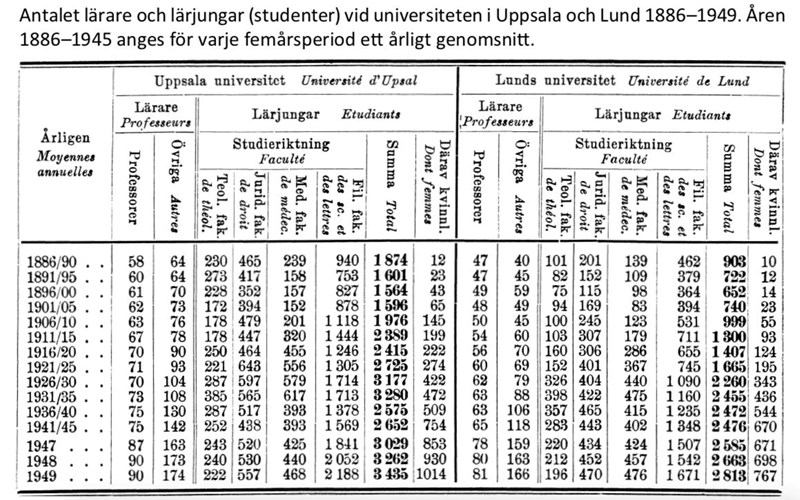
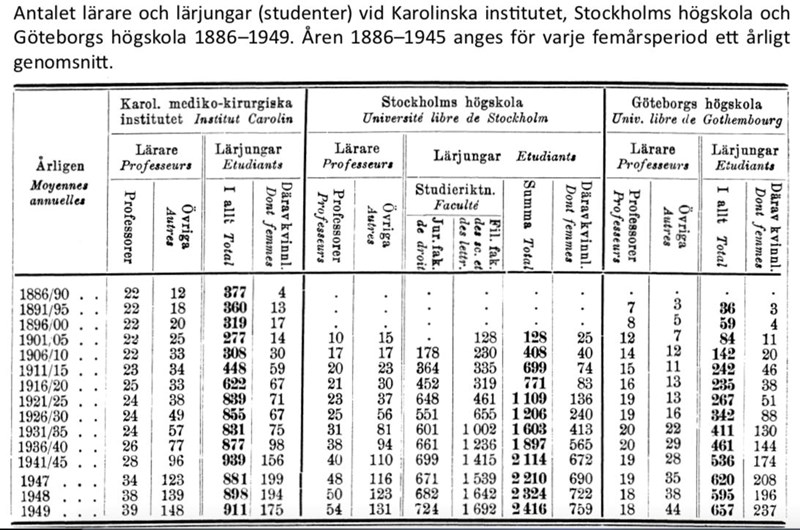
38. Hur stort var det årliga antalet studenter vid de fem lärosätena sammanlagt 1911/15?
A: 3 689
B: 4 607
C: 5 078
D: 5 549
Markera de relevanta områdena i tabellen:
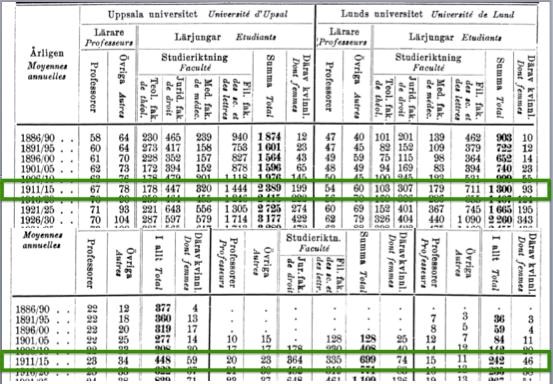
Approximativt räknat kan vi säga att antalet studenter var stycken. Detta är väldigt nära alternativ C, 5 078.
Svar: C, 5 078.
39. Hur stor andel av lärarna vid Göteborgs högskola 1949 var professorer?
A: 30 procent
B: 40 procent
C: 60 procent
D: 70 procent
Det totala antalet lärare fås genom att summera antalet professorer och övriga:

Det totala antalet lärare är stycken. Av dessa 62 är 18 personer professorer. Detta ger andelen:
Drygt 30%.
Svar: A, 30 procent.
40. Vilket lärosäte hade minst antal studenter per lärare 1947?
A: Lunds universitet
B: Karolinska institutet
C: Stockholms högskola
D: Göteborgs högskola
Denna uppgift kräver en del beräkningar, tyvärr.
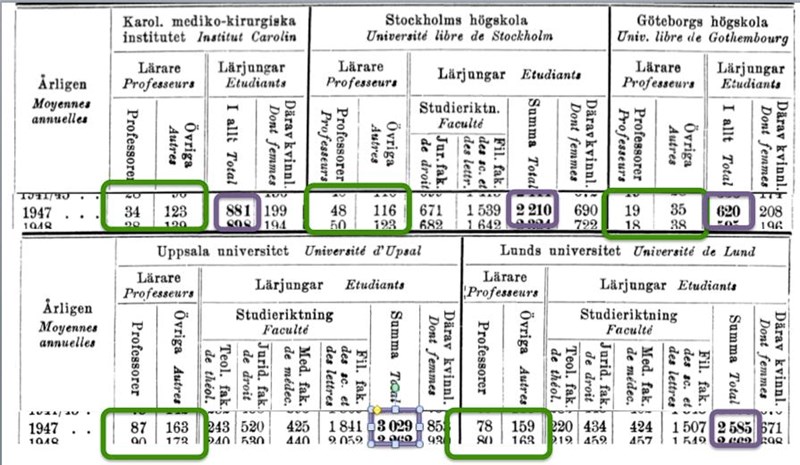
Vi kan dock göra det lite lättare med hjälp av en tabell:
En överslagsräkning av antalet lärare ger tabellen:
För att få så få elever per lärare som möjligt, vill vi att antalet studenter och antalet lärare ska vara så nära varandra som möjligt. Karolinska har fler lärare och mycket färre elever än Stockholm har. Alltså kan Stockholms högskola inte vara rätt svar. För att spara tid, och slippa räkna så mycket, kan vi kika på vad som händer om vi dubblerar antalet studenter och lärare på Karolinska. Förhållandet bevaras då, men vi får drygt 1700 studenter på 320 lärare. Detta är långt fler lärare, och långt färre studenter, än Lunds högskola har. Därmed kan vi stryka Lunds högskola.
Slutligen kan vi dividera antalet studenter och lärare på Karolinska med tre, för att få ut ungefär hur Karolinska kan jämföras med Göteborg. Då får vi att Karolinska skulle ha knappt trehundra elever på ungefär femtiofem lärare. Karolinska har långt färre studenter per lärare, än Göteborg har. Då kan vi konstatera att svaret är att Karolinska hade minst antal studenter per lärare.
Svar: B, Karolinska institutet.
Åttio uppgifter senare var det dags för mig att lägga ned pennan. Hoppas det har varit till någon nytta för er. Om något blivit knas, skriv jättegärna i tråden eller skicka ett PM. Om ni har förslag på alternativa lösningar, skriv dem här! :)
Smutstvätt skrev:Kvantitet I:
Kvantitet II:
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräckligHär är det svårt att hitta något bra räknetips, men genom att använda parenteser kan man spara lite tid åtminstone:
Svar: A, I är större än II.
Räknetips: Konjugatregeln. Om man begriper den så ser man svaret direkt.
(100+x)(100-x) blir större ju mindre x är (till och med noll om någon vill vara petnoga :P). I kvantitet 1 är x 1 och i kvantitet 2 är x 2.
pelleplums skrev:Smutstvätt skrev:Kvantitet I:
Kvantitet II:
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräckligHär är det svårt att hitta något bra räknetips, men genom att använda parenteser kan man spara lite tid åtminstone:
Svar: A, I är större än II.Räknetips: Konjugatregeln. Om man begriper den så ser man svaret direkt.
(100+x)(100-x) blir större ju mindre x är (till och med noll om någon vill vara petnoga :P). I kvantitet 1 är x 1 och i kvantitet 2 är x 2.
Smart, det tänkte jag inte på. Jag lägger till det!
Smutstvätt skrev:Vilket av svarsalternativen motsvarar uttrycket ?
A:
B:
C:
D:Multiplicera alla termer i den ena parentesen med alla termer i den andra. Detta är ofta lättast att göra visuellt:
Förenkling av dessa termer ger att .
Svar: C, .
Hur fick du det till a^2 ?
Fysikguden1234 skrev:Smutstvätt skrev:Vilket av svarsalternativen motsvarar uttrycket ?
A:
B:
C:
D:Multiplicera alla termer i den ena parentesen med alla termer i den andra. Detta är ofta lättast att göra visuellt:
Förenkling av dessa termer ger att .
Svar: C, .
Hur fick du det till a^2 ? Detta är ju ett fel
Ursäkta mig, en sexa hade försvunnit. Det är rättat nu, tack för dina hökögon! :)
Smutstvätt skrev:Vad är m?
A: -1
B: 0
C: 1
D: 2Sätt in i f(x). Då fås:
Alltså måste m vara lika med -
1, för att påstående två ska stämma.
Svar: A, -1.
wtf ....hur?
Mir022 skrev:Smutstvätt skrev:Vad är m?
A: -1
B: 0
C: 1
D: 2Sätt in i f(x). Då fås:
Alltså måste m vara lika med -
1, för att påstående två ska stämma.
Svar: A, -1.wtf ....hur?
Vad är det du undrar över?
Smutstvätt skrev:En cirkel är placerad i ett koordinatsystem. AB är cirkelns diameter. Cirkelns medelpunkt har koordinaterna (−2, 1) och A har koordinaterna (−4, −2). Vad är koordinaterna för B?
A: (4, 0)
B: (0, 4)
C: (4, 2)
D: (2, 4)
Borde inte x,y vara lika med 0,0? Alltså origo
Rita upp en ungefärlig bild!
Avståndet i x- och y-led måste vara lika stort mellan den givna punkten och mitten, som mellan mitten och den motstående punkten. Avståndet i x-led mellan den givna punkten och mitten är 2 steg. Alltså är x-koordinaten för den motstående, sökta punkten, lika med noll. Då kan vi sluta oss till att alternativ B är det rätta.
Svar: B, (0, 4)
Gissa vem som varit lite stressad när jag skrev dessa lösningar? Koordinaten till A ska vara (-4, -2). Slutsatsen är dock korrekt.
Smutstvätt skrev:Hur stor är vinkeln x?
A: 28°
B: 32°
C: 38°
D: 42°Genom att utnyttja att trianglarna överlappar varandra, kan vi konstatera att den blå vinkeln i bilden nedan är den vinkel vi kommer att behöva ta fram för att kunna beräkna x:
En triangel har alltid vinkelsumman 180 grader. Med hjälp av den uppgiften kan vi få fram att den grönmarkerade vinkeln är 70 grader stor. Vinkelsumman i en fyrhörning är alltid 360 grader, och då kan vi få fram att den blåa vinkeln är 56 grader. Slutligen kan vi då beräkna x, och få fram att x är 42 grader.
Svar: D, 42 grader.
Det finns en lättare lösning
Fysikguden1234 skrev:Smutstvätt skrev:En cirkel är placerad i ett koordinatsystem. AB är cirkelns diameter. Cirkelns medelpunkt har koordinaterna (−2, 1) och A har koordinaterna (−4, −2). Vad är koordinaterna för B?
A: (4, 0)
B: (0, 4)
C: (4, 2)
D: (2, 4)
Borde inte x,y vara lika med 0,0? Alltså origo
Rita upp en ungefärlig bild!
Avståndet i x- och y-led måste vara lika stort mellan den givna punkten och mitten, som mellan mitten och den motstående punkten. Avståndet i x-led mellan den givna punkten och mitten är 2 steg. Alltså är x-koordinaten för den motstående, sökta punkten, lika med noll. Då kan vi sluta oss till att alternativ B är det rätta.
Svar: B, (0, 4)
Borde inte x,y vara lika med 0,0? Alltså i origo
Fysikguden1234 skrev:Fysikguden1234 skrev:Smutstvätt skrev:En cirkel är placerad i ett koordinatsystem. AB är cirkelns diameter. Cirkelns medelpunkt har koordinaterna (−2, 1) och A har koordinaterna (−4, −2). Vad är koordinaterna för B?
A: (4, 0)
B: (0, 4)
C: (4, 2)
D: (2, 4)
Borde inte x,y vara lika med 0,0? Alltså origo
Rita upp en ungefärlig bild!
Avståndet i x- och y-led måste vara lika stort mellan den givna punkten och mitten, som mellan mitten och den motstående punkten. Avståndet i x-led mellan den givna punkten och mitten är 2 steg. Alltså är x-koordinaten för den motstående, sökta punkten, lika med noll. Då kan vi sluta oss till att alternativ B är det rätta.
Svar: B, (0, 4)Borde inte x,y vara lika med 0,0? Alltså i origo
Nej, men den nedre punkten bore ha haft koordinaterna (-4,-2) och då blir (x,y) lika med (0,4) precis som Smutstvätt/pepparkvarn skrev för 12 timmar sedan.
Smaragdalena skrev:Fysikguden1234 skrev:Fysikguden1234 skrev:Smutstvätt skrev:En cirkel är placerad i ett koordinatsystem. AB är cirkelns diameter. Cirkelns medelpunkt har koordinaterna (−2, 1) och A har koordinaterna (−4, −2). Vad är koordinaterna för B?
A: (4, 0)
B: (0, 4)
C: (4, 2)
D: (2, 4)
Borde inte x,y vara lika med 0,0? Alltså origo
Rita upp en ungefärlig bild!
Avståndet i x- och y-led måste vara lika stort mellan den givna punkten och mitten, som mellan mitten och den motstående punkten. Avståndet i x-led mellan den givna punkten och mitten är 2 steg. Alltså är x-koordinaten för den motstående, sökta punkten, lika med noll. Då kan vi sluta oss till att alternativ B är det rätta.
Svar: B, (0, 4)Borde inte x,y vara lika med 0,0? Alltså i origo
Nej, men den nedre punkten bore ha haft koordinaterna (-4,-2) och då blir (x,y) lika med (0,4) precis som Smutstvätt/pepparkvarn skrev för 12 timmar sedan.
Såg det nu. Jag kollade på bilden och det ska stå -2 och inte 2
Fysikguden1234 skrev:Smutstvätt skrev:Hur stor är vinkeln x?
A: 28°
B: 32°
C: 38°
D: 42°Det finns en lättare lösning
Vad kul! Skriv gärna den här i tråden!
pepparkvarn skrev:Fysikguden1234 skrev:Smutstvätt skrev:Hur stor är vinkeln x?
A: 28°
B: 32°
C: 38°
D: 42°Det finns en lättare lösning
Vad kul! Skriv gärna den här i tråden!
Vinkelsumman för en triangel är 180°. Vi kan räkna ut vinkeln alpha genom att ta 180 - (82+28) = 70°. Samtidigt vet vi att vinkelsumman för en rak linje också är 180°. Vi kan då räkna ut vinkel beta genom att ta 180 - 152 = 28°. Eftersom att vi vet vinkel alpha som är 70° kan vi även räkna ut vinkel V genom att ta 180 - 70 = 110°. I den lilla triangeln har vi nu vinklarna 110 och 28 vilket tillsammans blir 138°. För att räkna ut x tar vi 180 - 138 = 42°
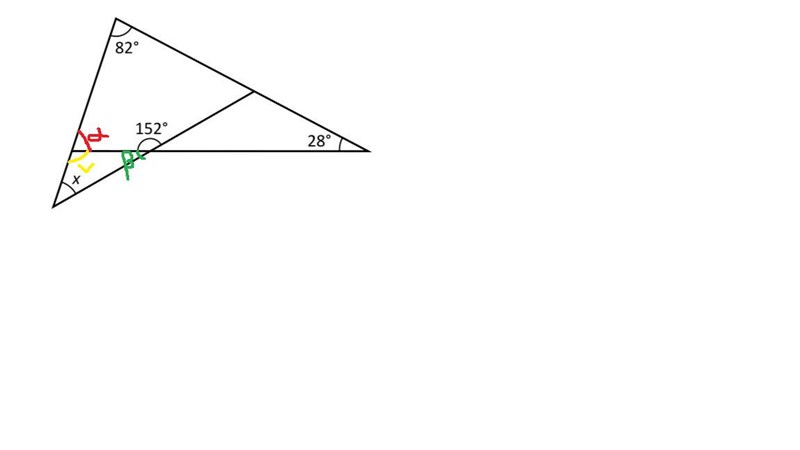
Alltid bra med flera olika lösningar.
Men lättare?
x+y
Välkommen till Pluggakuten, BarlinLany! Hur menar du med "x+y"? :)
Vinkelsumman för en fyrhörning är 360 grader.
x+82+28+(360-152)=360
x = 152-28-82 =42
Smutstvätt skrev:ABCD är en rektangel och AFD är en triangel. Hur lång är DE?
A: 5 cm
B: 6 cm
C: 7 cm
D: 8 cm
Det är lätt att börja tänka "likformighet", när denna typ av uppgifter kommer, men det är lönlöst i detta fall. När du ser en rätvinklig triangel, börja med att tänka "Pythagoras sats". Den ger oss nämligen att hypotenusan i den stora rektangeln, sträckan DF, är tio centimeter lång. Då måste sträckan DE vara (cm) lång.
Svar: B, 6 cm.
Hej, kan du förklara det jag markerade med fet stil?
Edit: Never mind, du fick 10:an ifrån Pythagoras sats.
Smutstvätt skrev:För en viss parallellogram gäller att vinkeln i ett av hörnen är 57°.
Kvantitet I: Vinkeln i ett av de andra hörnen i parallellogrammen
Kvantitet II: 124°
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Ett parallellogram är en rektangel som knuffats åt sidan. Det betyder att motstående vinklar alltid är lika stora, men inte nödvändigtvis nittio grader. Eftersom vinkelsumman i alla fyrhörningar är 360 grader, kan de andra två vinklarna, v, beräknas:
Kvantitet II var 124 grader, och är alltså större än alla vinklar i parallellogrammen. Då kan vi sluta oss till att II är större än I.
Svar: B, II är större än I.
Ett av de andra hörnen kan ju också betyda det hörnet med vinkeln 57 grader ???????
Det är sant! Dock spelar det ingen roll i detta fall, då vinkeln 57 grader ändå är mindre än kvantitet II. Detta konstateras lite i all hast där det står
Kvantitet II var 124 grader, och är alltså större än alla vinklar i parallellogrammen.
i slutet. Men det är lite otydligt. Jag lägger till en kommentar med ett förtydligande! :)
Smutstvätt skrev:
Kvantitet I: Arean av den skuggade ytan
Kvantitet II:
A I är större än II
B II är större än I
C I är lika med II
D informationen är otillräcklig
Eftersom triangeln är likbent, är de streckade linjerna också 2 cm långa. Därför måste den skuggade triangelns sidor vara cm långa, och arean av det skuggade området måste då vara . Då vet vi att den första kvantiteten är större än den andra.
Svar: A, I är större än II.
Hej! Varför innebär det faktum att triangeln är likbent att de streckade linjerna är 2 cm långa?
(Jag uppskattar förresten verkligen att du tagit dig tiden att gå igenom och förklara några av högskoleproven, det är till stor hjälp!)
Eftersom triangeln är rätvinklig och likbent är de spetsiga vinklarna 45 grader.
Det gäller både triangeln med sidorna 8 och den med sidorna 2.
En rätvinklig triangel där de spetsiga vinklarna är 45 grader är likbent.






