Hur använder man Navier-Stokes för att förenkla?
Hej!
Jag håller på att läsa härledningen av "the energy equation" i fluiddynamik, och har ett litet problem med en av förenklingarna. Se bild nedan.
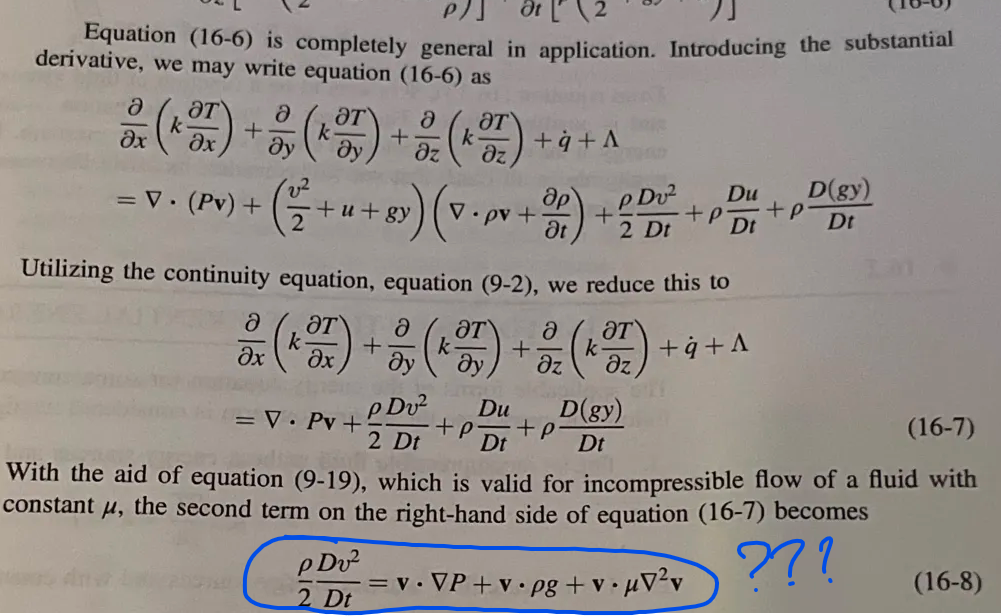
Equation 9-19 är den vanliga formen av Navier-Stokes för inkompressibla flöden med konstant viskositet, alltså
Hur har man använt den här ekvationen? Var kommer alla hastighetsvektorer i HL till 16-8 ifrån?
Är du med på att
Alltså är det bara det "vanliga" vänsterledet i Navier-stokes skalärmultiplicerat med , ser du?
Ah, där ser man! Jag kände inte till den identitieten men det är ju enkelt att verifiera.
Jag måste ta lite tid till att verifiera det vid tillfälle. Återkommer.
Tack så mycket tills dess!
Ja, räknetekniskt är det en produktregel för "derivatan", men det kan kännas lite skumt eftersom det är vektorer och dessutom en lite "konstig" materiederivata. Men det är alltså den helt vanliga Jakobiregeln.
Ja precis, jag har inte riktigt hunnit bekanta mig ordentligt än med "materiederivatan". Jag hade aldrig sett den innan den dök upp i boken häromdagen :)
En liten grej vid sidan om, visst stämmer det att definitionen av materiederivatan är
Det finns ingen definition i boken och det jag hittar på nätet (Wikipedia) verkar inte riktigt vara det man menar i boken. Hur tänker man i så fall med tiden som oberoende variabel? Vi har ju allmänt för fluidhastighet . Gör inte nablaoperatorn att man får med en tidsderivata för mycket, eller verkar denna endast på rumskoordinaterna,
så att man "struntar" i tiden då man bildar vektorn?
Ja, nablaoperatorn verkar bara på rumskoordinaterna. Vi skiljer mellan tid och rum.
När det gäller derivatan har kärt barn har många namn, ibland kallar man den substansderivata eller substantive derivative.
Jag är ganska säker på att ni har med den i er bok och jag tycker att du ska försöka hitta den! Men låt oss göra en informell härledning. Om vi till exempel har en temperatur och vill veta hur mycket den ändras under en liten tid kan vi skriva det som
Om vi nu delar med tiden får vi alltså en approximation av hur temperaturen ändras per tidsenhet när vi flyttar oss en liten sträcka under en liten tid:
'
Låt oss införa hastigheten , och gå i gräns. Då ser vi att vi kan uttrycka förändringen per tidsenhet som
Med lite mer rigörösa metoder kan man visa att det går alldeles utmärkt att definiera en operator (som fungerar för såväl skalära fält som tensorer)
Om man låter den verka på istället för får man exakt det uttryck du tar som "definition", men man kan alltså låta den verka på andra saker också. Vi låter den verka på :
Sammanfattningsvis kan man säga att det är en operator som kombinerar två sätt på vilket temperaturen (eller något annat, till exempel hastigheten) kan förändras. Den kan ändras för att temperaturen för hela fältet ändras, och då ändras temperaturen trots att vi inte rör oss i rumskoordinaterna det minsta. Temperaturen kan också ändras för att vi rör oss från en punkt till en annan punkt i fältet (och då spelar det såklart stor roll med hur stor hastighet vi rör oss från den ena punkten till den andra).


