Hur har dom paramatiserat linjestycket?
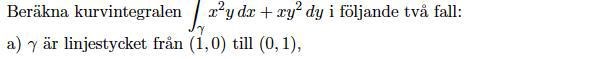
Lösning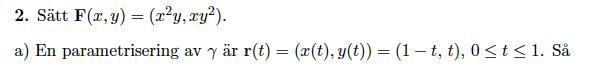
1) Hur de har fått (1-t,t)
Jag tänker: A=(1,0) och B=(0,1).
AB=B-A=(0,1)-(1,0)=(-1,1)
x=t ger då (t,1)-(t,0) = (0t,1)
Näe..
2) kan man lösa detta utan att hålla på att paramtisera. Typ Greens formel?
Du har redan en tråd om den här frågan. Det är inte tillåtet att posta mer än en tråd om samma fråga. Om du fortsätter att bryta mot Pluggakutens regler, riskerar du avstängning. Tråden låses. /moderator
Den räta linje som går genom punkterna (1,0) och (0,1) har ekvationen som skulle ge parametriseringen (t,1-t), 0<t<1 men då kommer linjen att gå åt fel håll. Man kan lika gärna skriva räta linjens ekvation som x=1-y, och det är så de har tänkt i facit.
Du kan klara dig utan parametrisering, om jag tänker rätt. Om du ersätter y i respektive med 1-x har du bara en variabel kvar. Tänk på att räkna om dy!
De får fram parametriseringen genom att sätta (x,y)=A+t(B-A). t går då från 0 till 1.
Smaragdalena skrev:Den räta linje som går genom punkterna (1,0) och (0,1) har ekvationen som skulle ge parametriseringen (t,1-t), 0<t<1 men då kommer linjen att gå åt fel håll. Man kan lika gärna skriva räta linjens ekvation som x=1-y, och det är så de har tänkt i facit.
Jag är med på hur linjen ser ut. Men hänger nog inte med på hur du paramatiserat.
du har satt x=t? eller? ;sS
Vil du visa? =(
Jag vill att parametern skall ge koordinaterna , att parametern skall ge koordinaterna och att parametervärdena däremellan skall ge koordinater som uppfyller sambandet .
Det enklaste sätt jag kan komma på att få fram detta är att sätta koordinaterna till , .
(Det hade gått precis lika bra att parametrisera linjen som , eller , men det känns som att krångla till det i onödan.)
Om du kan förklara vad det är i detta som är svårt, så kan jag försöka förklara ännu mer.
Smaragdalena skrev:Jag vill att parametern skall ge koordinaterna , att parametern skall ge koordinaterna och att parametervärdena däremellan skall ge koordinater som uppfyller sambandet .
Det enklaste sätt jag kan komma på att få fram detta är att sätta koordinaterna till , .
(Det hade gått precis lika bra att parametrisera linjen som , eller , men det känns som att krångla till det i onödan.)
Om du kan förklara vad det är i detta som är svårt, så kan jag försöka förklara ännu mer.
Okej! Men varför skall just t=0 ge (1,0) och inte tex t=1 (och vise versa)
Okej! Men varför skall just t=0 ge (1,0) och inte tex t=1 (och vise versa)
För att du skall ha det så enkelt som möjligt när du beräknar kurvintegralen.
Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Albiki skrev:Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Hej Alkibi, =)
Var fick du ifrån?
mrlill_ludde skrev:Albiki skrev:Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Hej Alkibi, =)
Var fick du ifrån?
Den räta linjen som går genom punkterna och har riktningsvektorn .
Albiki skrev:mrlill_ludde skrev:Albiki skrev:Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Hej Alkibi, =)
Var fick du ifrån?Den räta linjen som går genom punkterna och har riktningsvektorn .
Hur får man fram det? (ja vet ju att det är så liksom för jag kan se, men vill bara se det matematiks)
Riktningsvektorn är samma sak som skillnadsvektorn mellan de två punkterna:
mrlill_ludde skrev:Albiki skrev:Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Hej Alkibi, =)
Var fick du ifrån?
Och så har du satt varför just
förlåt att jag är så trög
mrlill_ludde skrev:mrlill_ludde skrev:Albiki skrev:Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Hej Alkibi, =)
Var fick du ifrån?Och så har du satt varför just
förlåt att jag är så trög
För att i Albikis kombinerade parametrisering (x, y) av gamma så är x = 1 + t*(-1).
Laguna skrev:mrlill_ludde skrev:mrlill_ludde skrev:Albiki skrev:Hej!
Den orienterade kurvan startar i punkten och slutar i punkten ; det är därför lämpligt att använda en parameterisering som respekterar denna orientering.
Med hjälp av denna parameterisering reduceras kurvintegralen till en enkelintegral över intervallet
Hej Alkibi, =)
Var fick du ifrån?Och så har du satt varför just
förlåt att jag är så trög
För att i Albikis kombinerade parametrisering (x, y) av gamma så är x = 1 + t*(-1).
Ja ja. Juste för AB=B-A=(0,1)-(1,0)=(-1,1) . Slarvade och ränade A-B. =)
Men då är jag med.Men det är ju densamma då som y?
Tack allihopa!
Ska läsa igenom alla inlägg, tänka, och kolla mer uppgifter. Hehe, på återseende!=)




