Hur löser man denna kurvintegral?
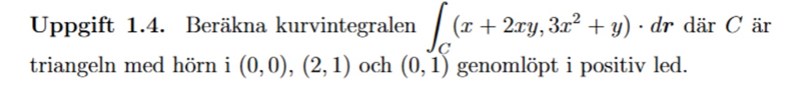
Vad har ni för definition av kurvintegralen? Kan detta svar vara till hjälp? :)
Helatan skrev:
Börja med att parameterisera triangeln. Finns det inget löst exempel i boken?
Trinity2 skrev:Helatan skrev:
Börja med att parameterisera triangeln. Finns det inget löst exempel i boken?
Finns inget svar i boken. Hur ska jag parametrisera triangeln?
Helatan skrev:Trinity2 skrev:Helatan skrev:
Börja med att parameterisera triangeln. Finns det inget löst exempel i boken?
Finns inget svar i boken. Hur ska jag parametrisera triangeln?
Svar är en sak, men ingen bok kan väl kräva att du skall fundera ut hur detta går till utan teori och exempel?
Jag hade delat upp det i 3 sträckor
(x,y)=(t,t/2), 0≤t≤2
(x,y)=(2-t,1), 0≤t≤2
(x,y)=(0,1-t), 0≤t≤1 eller (x,y)=(0,1-t/2), 0≤t≤2 om du vill ha samma t-gränser
om jag förstod kurvan rätt.
(Svaret är 8/3)
Trinity2 skrev:Helatan skrev:Trinity2 skrev:Helatan skrev:
Börja med att parameterisera triangeln. Finns det inget löst exempel i boken?
Finns inget svar i boken. Hur ska jag parametrisera triangeln?
Svar är en sak, men ingen bok kan väl kräva att du skall fundera ut hur detta går till utan teori och exempel?
Uppgiften kommer inte från någon bok utan från veckans häfte, vilket innehåller en kort sammanfattning och några uppgifter. Kursboken är Adams Calculus, där det finns flera lösta exempel (men tyvärr på engelska). Dessutom innehåller faktiskt häftets facit såväl svaret som ledtråden "Dela upp triangeln i räta linjestycken och parametrisera".
Mattetjejn skrev:Trinity2 skrev:Helatan skrev:Trinity2 skrev:Helatan skrev:
Börja med att parameterisera triangeln. Finns det inget löst exempel i boken?
Finns inget svar i boken. Hur ska jag parametrisera triangeln?
Svar är en sak, men ingen bok kan väl kräva att du skall fundera ut hur detta går till utan teori och exempel?
Uppgiften kommer inte från någon bok utan från veckans häfte, vilket innehåller en kort sammanfattning och några uppgifter. Kursboken är Adams Calculus, där det finns flera lösta exempel (men tyvärr på engelska). Dessutom innehåller faktiskt häftets facit såväl svaret som ledtråden "Dela upp triangeln i räta linjestycken och parametrisera".
Finns det liknande uppgifter lösta i boken? Den här typen av uppgifter måste man räkna minst 10-20 av innan man "fattar" hur man skall lösa dem. De är enkla när man väl förstår vad det står och vad de menar.
Är du (TS?) med på parameteriseringen ovan?
Trinity2 skrev:Mattetjejn skrev:Trinity2 skrev:Helatan skrev:Trinity2 skrev:Helatan skrev:
Börja med att parameterisera triangeln. Finns det inget löst exempel i boken?
Finns inget svar i boken. Hur ska jag parametrisera triangeln?
Svar är en sak, men ingen bok kan väl kräva att du skall fundera ut hur detta går till utan teori och exempel?
Uppgiften kommer inte från någon bok utan från veckans häfte, vilket innehåller en kort sammanfattning och några uppgifter. Kursboken är Adams Calculus, där det finns flera lösta exempel (men tyvärr på engelska). Dessutom innehåller faktiskt häftets facit såväl svaret som ledtråden "Dela upp triangeln i räta linjestycken och parametrisera".
Finns det liknande uppgifter lösta i boken? Den här typen av uppgifter måste man räkna minst 10-20 av innan man "fattar" hur man skall lösa dem. De är enkla när man väl förstår vad det står och vad de menar.
Lösta exempel av kurvintegraler med parametrisering, ja, inklusive med räta linjestycken - men just nu hittar jag inget exempel med en triangel, om det var så du mena. Om TS hade sett ledtråden i facit hade det kanske varit lättare, för den svarar på frågan "Hur ska jag parametrisera triangeln?" Sammanlagt i boken och häftet finns det även många uppgifter att räkna själv (och meningen med häftet är att man jobbar med det under en workshop där en assistent finns där för att hjälpa till, men jag vet inte om TS går på workshops eller inte).
Beroende på lärare kan man även ha sett sådana exempel under föreläsningarna.


