Hur ska man beräkna ångbildningsentalpin när systemet inte är i jämvikt?
Halloj!
Jag sitter med en gammal tentauppgift:
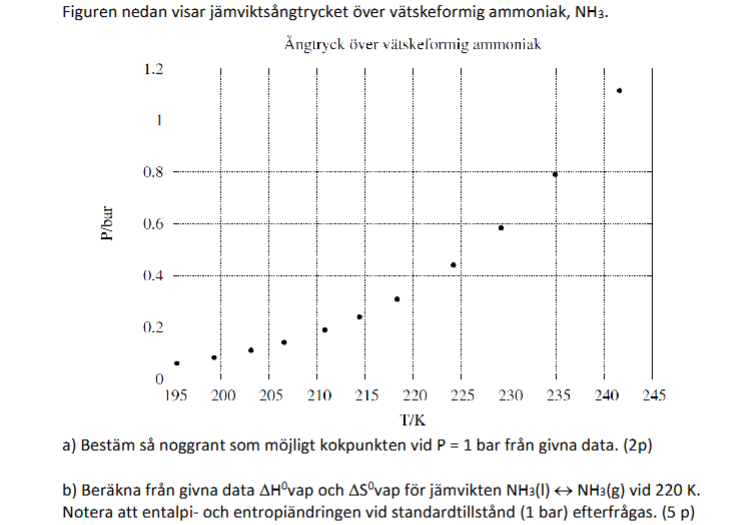
Hur i hela friden ska man ta sig an (b)?! Det står att man ska beräkna ångbildningsentalpin då ammoniak står i jämvikt med sin ånga vid 1 bar och 220 K. Men jag ser ju i grafen att det inte finns en jämvikt som ligger på både 1 bar och 220 K. Så hur ska man göra?
Jag hade ritat en tangent till kurvan vid den angivna temperaturen och utifrån den beräknat förångningsentalpin med Clausius-Clapeyrons ekvation. När du vet den kan du utnyttja att ändringen i Gibbs energi är 0 vid kokpunkten, vilket gör att du kan bestämma entropiändringen.
För att omvandla till värden vid standardtillstånd borde man kunna dela upp det hela i ett antal steg (Hess lag). Om jämviktstemperaturen vid 1 bar är T, kan man börja med att kyla vätskan från T till 220 K, sedan förånga vätskan vid 220 K och till sist värma ångan till T. Summerar du alla dessa steg borde det ge dig värdena vid standardtillstånd.
Tack för svar.
Jag kanske var lite otydlig i min fråga. Jag begriper inte ens vad som efterfrågas. Det står att man ska bestämma ångbildningsentalpin och ångbildningsentropin för jämvikten NH3(l) ⇌ NH3(g) vid 220 K och 1 bar. Men som vi ser i grafen är vätskeformig ammoniak inte i jämvikt med sin ånga vid de tillstånden. Hade det funnits en jämvikt vid 1 bar och 220 K hade det väl funnits en punkt inprickad där?
Standardtillstånd beskriver sällan ett verkligt tillstånd, det är bara en beräkningsbas för att kunna omvandla värden till sina faktiska tillstånd. Punkterna/kurvan i din figur visar det verkliga sambandet mellan ångtryck och temperatur för ammoniak. När man befinner sig på den kurvan befinner man sig också på kokpunkten.
Ja, det förstår jag. Så man ska "låtsas" att det finns en jämvikt mellan vätskeformig och gasformig ammoniak vid 1 bar och 220 K och beräkna vad ångbildningsentropin och ångbildningsentalpin då hade varit?
Ja, du kan tänka att du beräknar värdena för ett hypotetiskt tillstånd där ammoniak kokar vid 1 bar och 220 K. Det betyder inte att ammoniak faktiskt kokar vid dessa värden.
Okej. Bara så att kolla att jag förstår Clausius-Clapeyron rätt:
Vi har ju:
Förstår jag det rätt som att uttrycket relaterar ångbildningsentalpin vid en viss temperatur och ett mättnadstryck , trycket som systemet har vid vätske-gas-jämvikt, alltså trycket längs isotermen i tvåfasområdet i ett P-H-diagram?
I så fall borde man väl kunna integrera den här relationen och studera en differens? Om man väljer en punkt nära den önskade punkten borde väl ångbildningsentalpin vara typ konstant?
Jag brukar tänka att den anger sambandet mellan tryck och temperatur vid fasövergången, men det kanske är ekvivalent med din formulering.
Ja, det finns en integrerad form av Clausius-ekvationen, dock får man vara försiktig med ΔH, eftersom det över små temperaturintervall kan behandlas som en konstant, oberoende av temperaturen, men över större intervall är den rätt temperaturberoende vilket man måste ta hänsyn till vid integreringen. Lutningen hos din kurva beror på värdet hos ΔH, och eftersom lutningen ändras hos kurvan kan man också inse att ΔH ändras med temperaturen.
Jag brukar tänka att den anger sambandet mellan tryck och temperatur vid fasövergången, men det kanske är ekvivalent med din formulering.
Ja precis, jag tror att det är ekvivalent med hur jag tänker på det. Oavsett vilken kvalité vår ånga har kommer vara samma för samma , givet att vi alltid har någon ånga eller vätska kvar, eller hur?
Dessutom: kan man tänka att "mättnadstrycket" är samma sak som "ångtrycket vid jämvikt (vilket är samma som vätsketrycket)"?
Jag kunde inte hålla mig och tjuvkikade i facit. Så här har tentamakaren gjort där:

Kan inte säga att jag hänger med riktigt på vad som händer... Det är den integrerade Clausius-ekvationen där man har tagit en differens och antagit konstant ångbildningsentalpi (antar jag), men hur motiverar man val av datapunkter osv?
Vilken del av svaret är detta? Det kan inte vara hela svaret eftersom det är fler saker som efterfrågas. Håller med om att det ser ut som en förenkling, men lutningen hos en linje dragen mellan första och sista punkten motsvarar ungefär lutningen vid 220 K, så värdet på föråndningsentalpin vid kokpunkten runt trycket (ish) 0,4 bar borde ligga nära värdet i facit.
Oj, råkade missa en del av facit. Här är hela:

Ja, man gör ju ett antagande att ΔH är oberoende av temperaturen, känns tveksamt när man ser figuren. Enda sättet att se om antagandet är rimligt är nog att inte göra det antagandet, räkna som jag föreslog och sen jämföra svaren.
Jag hänger fortfarande inte riktigt med på hur man har gjort i facit (man kan ju inte anklaga examinatorn för att vara utförlig...)
Vi vill använda Clausius-Clapeyron för att uppskatta ångbildningsentalpin i ett tänkt tillstånd där vätskeformig ammoniak kokar vid 220 K och 1 bar. Vi har ekvationen
Hur använder vi sedan denna? Du nämner lutningar men jag är inte riktigt med på hur tangentlutningar kommer in i bilden.
Det blir tydligare när man har den på denna form:
 Vänsterledet beskriver lutningen hos kurvan du postade, dvs lutningen hos en tangent till kurvan vid temperaturen T.
Vänsterledet beskriver lutningen hos kurvan du postade, dvs lutningen hos en tangent till kurvan vid temperaturen T.
Okej.
Men jag förstår inte hur vi skulle kunna tillämpa denna på vårt hypotetiska tillstånd där ammoniak kokar vid 1 bar och 220 K. För att vi ska kunna räkna ut en lutning måste väl den punkten också ligga på kurvan?
Vi skulle väl i så fall behöva räkna ut lutningen i den röda punkten:
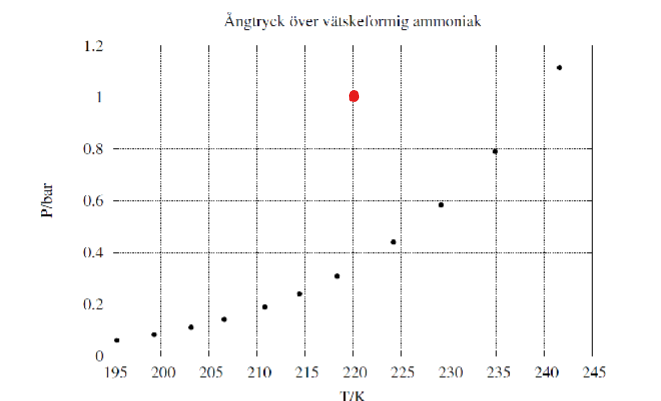
Men kurvan blir ju osammanhängande då eftersom (220 K, 1 bar) inte är en punkt som "finns på riktigt".
Du börjar med att räkna ut de faktiska värdena, dvs de som ligger på kurvan. Sedan räknar man om det till ett hypotetiskt värde vid standardtillstånd.
Okej, så man ska börja med att räkna ut lutningen i den riktiga punkten (alltså typ (220 K, 0.4 bar))?
Jo precis
Okej, men hur ska man hantera att det finns en volymförändring i nämnaren? När man väl har lutningen i den riktiga punkten (220 K, 0.4 bar). Låt säga att vi kommer fram till att lutningen i den punkten är . Då har vi:
Hur ska man tänka kring när vi löser ut ?
Du kan beräkna volymändringen vid förångningen. Det är skillnaden i molär volym mellan ammoniak som vätska respektive gas.
Skillnaden i molär volym? Kommer vi inte få enhetsfel då?
Det bör du inte få.
Eller jaha, vi får entalpi per mol förångad ammoniak då istället för "ren" entalpi med enhet joule.
Ja, troligen kan du dessutom försumma vätskans volym eftersom den bör vara mycket mindre än gasens volym. Volymändringen är alltså cirka gasens volym.
Okej, då tror jag att jag är med på hur man kan lösa uppgiften (givet att man kan slå upp molär volym för ammoniak vid given temperatur). Om vi antar en ideal gas kan vi skriva och använda värden ur grafen.
Men jag hänger ändå inte med på vad examinatorn har gjort i facit. Är det han tänker helt enkelt att ångbildningsentalpin är temperatur- och tryckoberoende och integrerar mellan två tryck och temperaturer? I så fall hade den väl varit samma "överallt"?
Det tycks vara så
Men då grafen faktiskt har icke-konstant lutning hade man väl fått olika värden på ångbildningsentalpin beroende på mellan vilka två punkter man integrerar?
Det borde bli så, men kontrollräkna gärna så kan vi verifiera det. Det kan hända att examinatorn bara har tur eftersom lutningen vid 220 K är rätt nära snittlutningen mellan första och sista punkten?
Okej, jag gör ett försök. Jag använder punkten (~218 K, ~0.3 bar) samt (~223 K, ~0.43 bar) och antar att lutningen mellan dessa är samma som lutningen i den äkta datapunkten vid 220 K:
Om vi antar att ångan är en ideal gas och att dess volym är mycket större än vätskans molära volym har vi
Så ganska nära.
Men sedan när han väl har sitt värde på ångbildningsentalpin och ska räkna om det till det tänkta standardtillståndet, använder han återigen samma antagande om temperatur- och tryckoberoende och säger att ångbildningsentalpin då måste vara samma i det tänktz tillståndet som i det han räknade på?
I så fall fattar jag inte vad han gör med entropin. Om ångbildningsentalpin är 26 kJ/mol (eller 23 kJ/mol som han fick) även i det tänkta referenstillståndet (eftersom entalpin tydligen är tryck, och temperaturoberoende), borde man inte kunna räkna ut entropin direkt genom
?
Jo så hade jag också gjort, när man befinner sig på jämviktskurvan vilket är samma sak som ditt samband fast omskrivet via .



