Hur ska man beräkna Norton- och Théveninekvivalenterna av denna krets?
Hej!
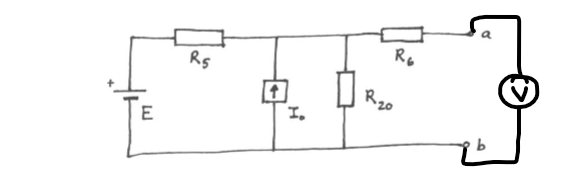
Jag sitter med uppgiften nedan:

Det första steget är att deaktivera alla källor och beräkna ersättningsresistansen sett från a och b. Då jag gjorde detta erhöll jag .
För Théveninekvivalenten behöver vi ju spänningen mellan a och b i den givna kretsen. Jag tänkte att man kunde potentialvandra från spänningskällan och beräkna det sammanlagda spänningsfallet över och , samt fallet över och ökningen över . Problemet är att jag inte vet hur man ska hantera att det sitter en strömkälla OCH en spänningskälla i kretsen. Lägger strömkällan på någon egen spänning?
Man kan även beräkna spänningen genom att hitta kortslutningsströmmen och sedan ta .
Ett annat tips är att thevenin-norton-omvandla E och R5 till en strömkälla med värde E/R5 parallellt med en resistor med värde R5.
Jag såg just en short om Théveninekvivalenter:
https://www.youtube.com/shorts/21bnMCGT5dw
Jag fattar inte riktigt en grej. Ska man ta med resistorn överhuvudtaget när vi räknar ut ersättningsresistansen för Théveninekvivalenten? Hon I videon räknar ju som om "hennes" inte existerar när hon räknar ut spänningen mellan a och b, men punkten a ligger väl "efter" (även om ingen ström går dit om kretsen inte är sluten i a)?
Resistansen som ska beräknas är mellan a och b när alla spänningskällor ersätts med kortslutning och strömkällor ersätts med ett avbrott.
I ditt fall blir resistansen R6 i serie med R5//R20 = 6+4 = 10 ohm
Spänningen mellan a och b är utan belastning, det går alltså ingen ström genom R6 så den påverkar inte utspänningen i det läget.
Från Wikipedia:
- Den ekvivalenta spänningen Vth är den spänning som kan mätas mellan A och B
- Den ekvivalenta resistansen Rth är den resistans som kan mätas mellan A och B om alla ideala spänningskällor ersätts med kortslutningar och alla ideala strömkällor ersätts med ledningsbrott
- Om A och B kopplas samman, är strömmen mellan A och B Vth/Rth (Rth kan beräknas som Vth dividerad med kortslutningsströmmen mellan A och B)
Men om vi skulle koppla på en voltmeter mellan a och b, vad hade den visat då? Hade den ens visat något?
Det går väl ingen ström alls i punkten a eftersom all ström borde gå ned genom . Så hur man kan göra en spänningsmätning mellan a och b?
Genom en ideal voltmeter går det ingen ström. När vi mäter över a till b så är strömmen genom R6 0 och därför är spänningen över R6 också noll, voltmetern känner därmed spänningen över R20.
Om vi antar att punkten b är jordad har du samma potential på bägge sidor om R6
Men hur kan spänningen mellan a och b vara samma som spänningen över när strömmen skulle vara tvungen att ta sig över för att nå a? Punkten a har väl en högre potential jämfört med spänningskällans minuspol än vad punkten innan har? För att nå a måste strömmen gå över ett motstånd "i fel riktning" och det borde väl höja potentialen jämfört med minuspolen?
Det går ingen ström genom R6 !
Spänning över motstånd uppstår när ström går genom dom.
Jmfr ohms lag U= R*I när I är 0 blir U också 0!
Jag håller med! Men hur kan vi ens göra en mätning i a om det inte går någon ström där? Voltmeterns ena ände sitter i en punkt utan ström.
Genom en verklig voltmeter går det ström, visserligen lite men i alla fall.
Ingångsimpedansen är i storleksordningen 10 Mohm i moderna instrument så de påverkar ytterst lite jämfört med den här kretsens utgångsresistans på 10 Ohm.
Om inget annat sägs brukar man anta att mätinstrument är ideala, dvs oändlig inimpedans vid spänninsmätning och 0 resistans vid strömmätning.
(Det finns metoder att mäta utan att ta någon ström ur kretsen men det lämnar vi därhän i den här uppgiften)
Det är jag med på.
Min fråga är rent teoretisk. Om vi skulle potentialvandra längs riktningen strömmen går i teorin får vi spänningsfall över alla resistorer - vi får en sänkning i potential jämfört med spänningskällans minuspol. Men om vi skulle vilja mäta spänningen mellan a och b, då hade ju strömmen behövt gå "åt fel håll" och då hade väl potentialen stigit?
Nu går ju inte strömmen över överhuvudtaget, så hur skulle en sådan mätning ens fungera teoretiskt? I punkten a är väl kretsen helt död?




