Hur ska man börja på denna ?
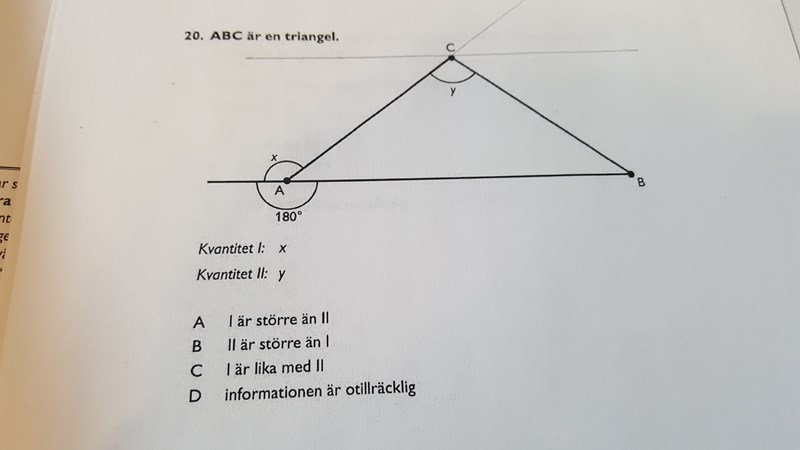 Har stött på fler sånna här och vet inte hur jag ska tackla en sådan uppgift. Det verkar inte finnas tillräckligt med info att lösa denna, men rätt svar ska vara A.
Har stött på fler sånna här och vet inte hur jag ska tackla en sådan uppgift. Det verkar inte finnas tillräckligt med info att lösa denna, men rätt svar ska vara A.
Det har att göra med vinkelsumman i en triangel, och ett halvt varv. Du vet att de båda är 180 grader. I triangeln på bilden finns tre vinklar: vid hörnen A, B och C (den vid C heter y i bilden).
Eftersom ett halvt varv är 180 grader vet du att "vinkeln vid A" + x = 180 grader.
Eftersom vinkelsumman i en triangel är 180 grader vet du att "vinkeln vid A" + "vinkeln vid B" + y = 180 grader.
Men då måste ju x = "vinkeln vid B" + y, och alltså är x större än y
Tänk att punkterna A och C är två fasta punkter.
Så förflyttar du punkten B horisontellt mot oändligheten :-)
Då ser du att vinkel-värdet hos y närmar sig vinkel-värdet hos x...men dom blir väl aldrig exakt lika!
Yosef skrev:
Har stött på fler sånna här och vet inte hur jag ska tackla en sådan uppgift. Det verkar inte finnas tillräckligt med info att lösa denna, men rätt svar ska vara A.
Kvantitet I: I vinkeln A i triangeln ovan ser du att: Vinkel x + Vinkel A = 180 grader
(Obs! Vinkel x + Vinkel A är sidovinklar och är därför 180* tillsammans)
Du vet att nu att Vinkel x + Vinkel a = 180 grader
Kvantitet II: Vinkel y + Vinkel B + Vinkel A = 180 grader. (Vinkelsumma för en triangel är alltid 180 grader)
Vinkel y = 180grader - Vinkel A - Vinkel B
y = 180 - a - b
Nu ser du att x är större än y. Därför är rätt svar A. Kvantitet I är större än kvantitet II.
Hej!
Vinkeln är en yttervinkel till triangeln ABC, vilket betyder att Vinkel ABC. Därför är .
Albikis svar är klockrent. Det spar mycket tid att kunna yttervinkelsatsen utantill.
ConnyN skrev:Albikis svar är klockrent. Det spar mycket tid att kunna yttervinkelsatsen utantill.
Frågan är vilket som går snabbast: att lära sig yttervinkelsatsen utantill, eller att klara sig ändå om man vet vinkelsumman i en triangel och att en rät linje motsvarar en vinkel på 180 grader. För mig funkar den andra metoden bäst, men vi är alla olika.
Smaragdalena skrev:ConnyN skrev:Albikis svar är klockrent. Det spar mycket tid att kunna yttervinkelsatsen utantill.
Frågan är vilket som går snabbast: att lära sig yttervinkelsatsen utantill, eller att klara sig ändå om man vet vinkelsumman i en triangel och att en rät linje motsvarar en vinkel på 180 grader. För mig funkar den andra metoden bäst, men vi är alla olika.
Det är ingen nackdel att känna till de två reglerna plus några till i geometrin. Min poäng och det jag upprepar är att högskoleprovet är inte svårt, men tiden är otroligt knapp. Det gäller att hela tiden kämpa mot klockan och varje sekund blir dyrbar. Att träna in sätt att få fram svaret fort är viktigt.
Jag gjorde så här (allt är vinklar i grader).
(180-x) +y + C = 180. => x=y+C.
Jag tänker då att man behövt lägga till C på y sidan för att få likheten i balans.
Därmed är x>y. (Vinkeln C är inte negativ)
---
Såg att Trådskaparen ritat in en parallell linje med nedre horisontella linjen, för att antagligen använda alternativvinklar och på så vis få ut att x=y. Funkar också.
Hinner inte skriva ner lösningen men den tog någon sekund längre (en förklaring kan vara angeläget för TS).
Snabbt utan figur och någon förklaring kan man säga att om
v1 = v2 => v1+x = 2* v2 + y => x = v1 + y dvs x>y






