Hur ska man förklara?
Hej! Jag håller på att försöka komma på en lösning till följande fråga:

Jag vet inte riktigt hur jag ska visa vad jag tänker och jag vet inte ens om min första tanke är rätt. Ett mönster jag såg var att första faktorn HL vad alltid 1 mindre än första faktorn i VL. Samtidigt var den andra faktorn alltid 1 större i HL än i VL. Jag har en känsla av att detta kanske har något med svaret att göra för det är ändå ett uppenbart mönster. Men om det är så, förstår jag inte riktigt logiken bakom det.
Känns som du är det något på spåren!
När det kommer till sådana här upg där man ska "visa att" handlar det ofta om att ställa utt ett generellt uttryck med en variabel som grund som liksom bevisar att svaret blir samma oavsett vilket värde man sätter variabeln till.
Vi provar:
Vi börjar med att skapa ett uttryck baserat på det första mönstret du såg. Om vi kallar den första faktorn i den första termen för n så kan vi försöka skriva uttryck för de andra faktorerna. Såhär
2*3 - 1*4 = 2
n*(n+1) - .....*..... (Testa själv att se om du förstår vad som ska stå här efter minus-tecknet baserat på att vi satt första faktorn som n. Facit finns i spoilern)
Visa spoiler
(n-1)*(n+2)
dvs uttrycket blir: n*(n+1) - (n-1)*(n+2)
Stämmer detta mönster för de övriga två beräkningarna? (I så fall är vi det något på spåren)
Kan du förenkla ditt uttryck på något sätt så att det bevisas att svaret alltid blir 2?
Wow det var mycket enklare än jag trodde! Jag löste det till och med innan jag kollade på spoilern! Men som du skrev så fick jag det till n*(n+1) - (n-1)*(n+2)
Efter det förenklade jag uttrycket till
Sedan gjorde jag det till en ekvation:
n2+n-n2-2n+n+2 =2
och när man förenklar allt ytterligare får man att 2=2
Snyggt jobbat!
Ett tips kan dock vara att tänka att i sådana här upg som säger "visa att" ska man aldrig använda sig av informationen som man ska bevisa! Vad menar jag med det?
Jo, i det här fallet ska vi bevisa att "man alltid får svaret/värdet 2". Därför får vi inte använda oss av informationen att uttrycket ska vara lika med 2 utan det är det vi istället vill komma fram till själva. Så istället för att ställa upp en ekv räcker det med att förenkla uttrycket och sedan konstatera att det kan förenklas till 2 (därför kommer uttryckets värde bli 2 oavsett värde på n). Vill man briljera lite extra kan man avsluta med förkortningen V.S.B som betyder vilket skulle bevisas - en matteterm man nästan alltid avslutar sådana här bevisnings-upg med.
Men nu var jag lite petig - för 9ans matte räcker din lösning gott och väl skulle jag tro! Men skadar inte med lite extra info :)
Verkligen inte! Tack för det. Då har man lärt sig något nytt också :)
KlmJan skrev:Verkligen inte! Tack för det. Då har man lärt sig något nytt också :)
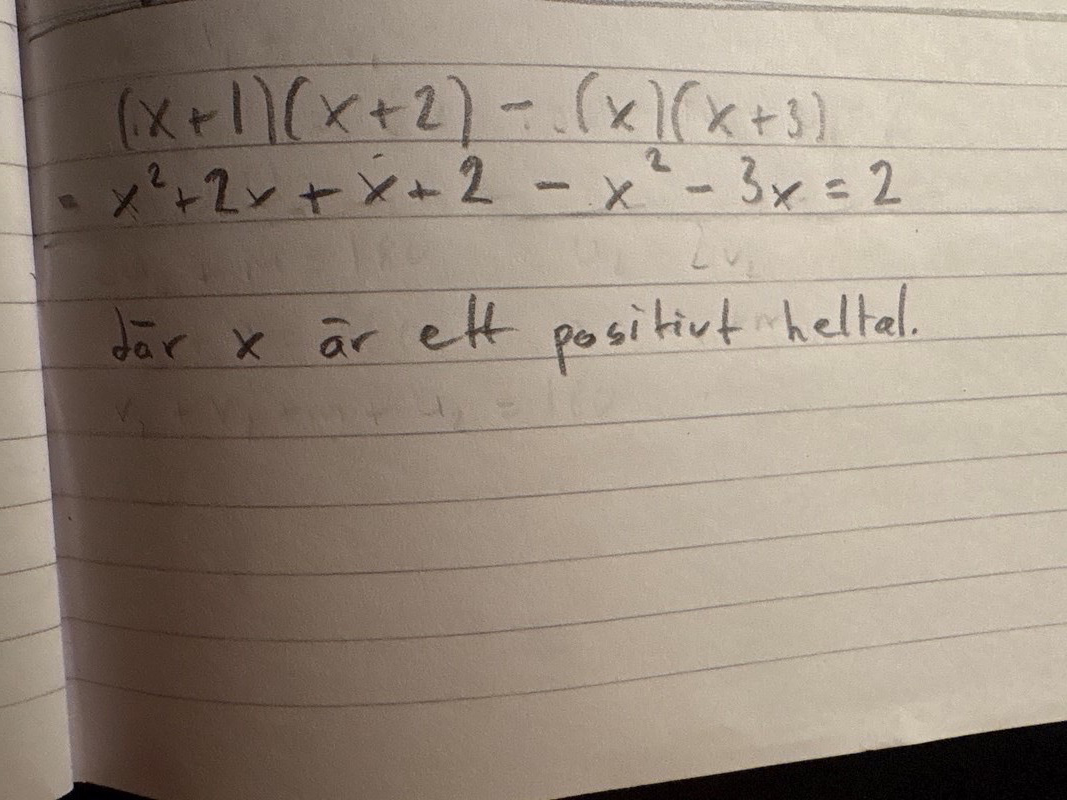
Själv hade jag använt mig av ett direktbevis där vi kan ställa upp ekvationen som ovan, förstår du hur vad jag gjort?
En vanligare symbol för att visa att ett bevis är fullbordat är .




