Hur ska man ställa upp flödesintegralen över ytan S?
Halloj!
Jag sitter med frågan nedan från en gammal tentamen i flervarabielanalys:
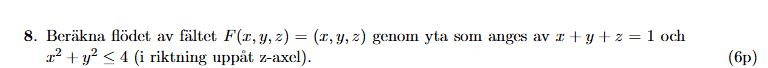
Jag antar att ytan, låt oss kalla den , är ytan som utgörs av snittet av planet och cylindern som definieras i uppgiften. Jag har försökt göra en skiss för lite visualisering:
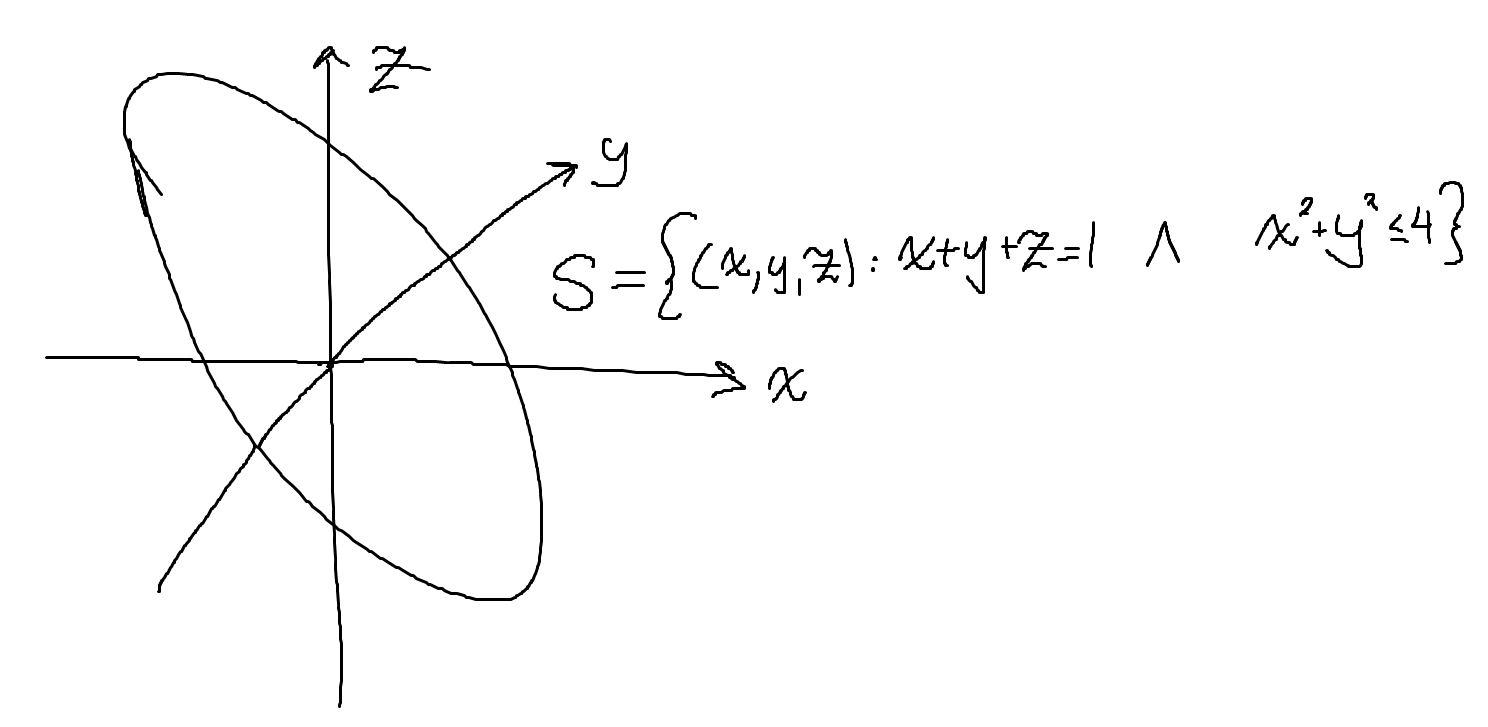
Tydligen är jag inte så bra på att rita men det är meningen att skivan ska "luta" på samma sätt som planet gör. Jag tolkar det som att jag ska ställa upp någon integral på formen:
Men hur ska man välja ? Jag antar att parantesen "(i riktning uppåt -axel)" ska ange hur ytan är orienterad men jag är inte helt med på hur man ska tolka det.
Riktning uppåt z-axel innebär att vi vill välja normalen till ytan så att z-elementet i uttrycket för normalen får ett positivt värde. (1,1,1) pekar i rätt riktning (-1,-1,-1) pekar i fel riktning. Tänk också på att få rätt normering för det du vill göra.
Eftersom ytan ligger i ett plan är det kanske inte jättesvårt att se vad normalen blir (den är dessutom konstant över hela ytan). Men för övning kan det vara nyttigt att
1. Parametrisera ytan
2. Bestäm dess normal (antingen med beräkning eller genom utantillkunskap om normalens utseende för din valda parametrisering)
Integralen du vill beräkna är alltså skalärprodukten av fältet och ytelementet
Okej, jag ger en parametrisering ett försök. Jag tänker att vi vill beskriva ytan med en vektorvärd funktion enligt . Eftersom "botten" till ytan är en cirkel med radie verkar det rimligt att vi sveper över denna i -planet och inför parametriseringen:
där och
Ser detta rätt ut? Jag är osäker på hur man bestämmer normalen när man väl har en parametrisering. Som du nämner råkar det ju vara lätt i just det här fallet eftersom det är "ett plan" men generellt vet jag inte hur man gör. Jag misstänker att det finns en kryssprodukt med någonstans i beräkningen eftersom vi vill ha en vinkelrät vektor.
Ytelementet avbildas vid denna transformation på:
Så det verkar rimligt (kanske?) att:
Men nu är jag ute på djupt vatten.
Det är helt korrekt! Snyggt! :-)
Att det fungerar så beror alltså på att enhetsnormalen ges av
Sätter vi ihop det med ditt uttryck för får vi
Men i just den här uppgiften kan det som sagt vara enklare att välja parameterframställningen
och med tillägget och sedan bekymra sig om vad det betyder senare.
Med en sådan parameterframställning i brukar man efter några uppgifter lära sig utantill att
Jag är lite förvirrad över vad vi ens har lyckats göra här. Vi kom fram till . Men vi behövde aldrig bekymra oss över vilken normal vi valde. Hur vet vi att vi räknade med "rätt" ?
EDIT:
och en grej till. Vi valde ju ordningen , men principiellt hade vi väl lika gärna kunnat ta ?
Ja, men tänk på att du skall välja den med positiv z-komponent enligt problemtexten.
Men hur vet man från början vilken ordning som blir rätt automatiskt?
Det kan vara lite knepigt att på förhand inse vilken som är rätt. Enklast är nog att välja en och kolla om det blir rätt riktning när man räknat klart. Om inte, så byt bara tecken på din framräknade normal.
Tolkar jag det rätt som att vi fick ut att enhetsnormalen är ?
Tillägg: 21 aug 2025 22:04
EDIT: ser nu att det såklart inte blir en enhetsnormal, utan endast EN normal.
Men hur som helst, om vi låter vara en funktion som ger enhetsnormalen till i varje punkt borde vi alltså ha:
för något område i -planet, eller hur?
Okej, jag tror jag hänger med. Vi har det orienterade ytelementet . är här enhetsnormalen till ytan i varje punkt . När vi sedan inför vår parametrisering avbildas på en annan vektor, och då slutar det vara relevant huruvida vektorn vi får är normal mot någon yta eller har längd 1, ty vi arbetar nu i ett enkelt tvådimensioellt område.
Är det rätt uppfattat?
Jag tror du har grepp om det nu, men jag blir lite stressad när du skriver att det slutar vara relevant huruvida vektorn vi får är en normal eller hur lång den är :-) Så för säkerhets skull tänker jag försöka knyta parameterframställningen med Jakobianen (som jag tror du börjar bli van vid).
Vektorn motsvarar första kolonnen i Jakobianen för den tvådimensionella avbildningen. Det är en basvektor för tangentplanet till ytan i punkten
Vektorn motsvarar andra kolonnen i Jakobianen. Det är den andra basvektorn till tangentplanet till ytan i punkten.
När du kryssar två vektorer får du en ny vektor som är vinkelrät mot båda vektorerna. I det här fallet får du alltså en vektor som är vinkelrät mot tangentplanet till ytan i punkten. Den "onormerade" normalen
har därmed exakt rätt längd för att kompensera avbildningen. Om du vill kan du istället se det som att du kryssar två differentialer för att se hur stor infinitesimal area de spänner upp
Om du ansätter din parameterframställning redan från början ska du alltså inte multiplicera med någon extra skalfaktor i din integral. Allt sköts av din parameterframställning. Om du däremot mellanlandar i får du först en skalfaktor i normalen och sedan eventuellt en "vanlig" Jakobian när/om du byter till polära (om du inte ser att det bara blir arean av en cirkel med radien 2 kvar) .
Slutligen, omvänd ordning av vektorerna i kryssprodukten innebär att normalen byter tecken. Det finns alltså en sorts automatisk orientering av ytan i den uppräkningsordning du väljer för dina parametrar.
Okej, så för att vara tydlig har vi alltså:
där är något område i -planet.
Det jag menade med att det inte spelar någon roll om vektorn vi får är "normal" eller "normerad" är att vektorn:
inte är normal mot något i -planet eller normerad. Är det korrekt uppfattat?
EDIT:
Och angående orientering, går det att veta från början vilken parameterordning som ger rätt orientering? I facit pratade de inte ens om ordning utan de bara körde på enligt omskrivningen ovan i det här inlägget (fast med en annan parametrisering).
Du skapar ett nytt -plan för varje punkt i din parameterframställning. Du har kommit fram till att en normal med exakt rätt längd för just din valda parameterframställning är för varje värde på . Din normalvektor är alltså helt vinkelrät mot varje -plan du skapar.
Vektorn och vektorn är alltid helt parallella eftersom du valt att låta löpa mellan 0 och 2 (vi kan bortse från vad som händer då ).
Vektorn har ett positivt z-element så länge du låter r ligga i ditt valda parameterintevall. Du har därmed orienterat ytan så att positiv riktning är "uppåt" z-axeln. Vidare har din vektor exakt rätt norm för vad du ska använda den till. Men den är inte normerad i bemärkelsen att , tvärtom varierar normen av vektorn över ditt parameterspann.
Som PATENTERAMERA påpekar kan det ibland vara mer praktiskt att räkna på och kontrollera att ytans normal har rätt orientering i efterhand. Skulle man ha råkat göra fel är det bara att byta uppräkningsordning eller tecken. Men basvektorerna utgör tillsammans med normalen ett högerorienterat system. På samma sätt som är . Det går att visualisera på förhand åt vilket håll normalen pekar.
Edit: Det slår mig nu i efterhand att du med -planet kanske menar parametermängden av -värden. Och i den betydelsen kan du se de det som att definitionsområdet eller punktmängden inte är "vinkelrät" mot något.
Det jag menade var att när vi gör vår substitution integrerar vi istället över ett enkelt 2D-område i -världen där och . Mot denna yta kommer aldrig vara vinkelrät, är vad jag menar. Visst stämmer det?
EDIT: men vad spelar det för roll att har positivt -element? Är det inte enhetsnormalen till ytan vi kräver ska ha positivt -element?
Ja, vi kan inte jämföra geometriska objekt mellan de olika mängderna.
är en kontinuerlig funktion from till . Definitionsområdet utgör ett slutet, begränsat område. Värdemängden för blir då en sammanhängande begränsad punktmängd i (närmare bestämt en yta). Ungefär så här:
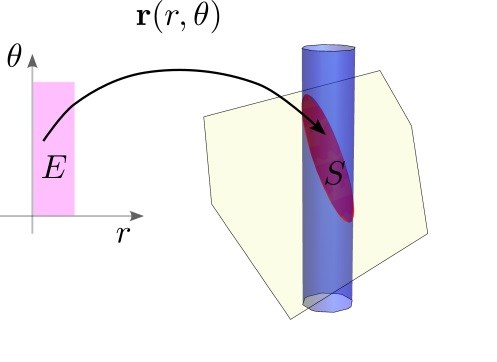
Det blir nonsens om vi ska prata om hur de olika mängderna och förhåller sig till varandra geometriskt eller hur vektorer i förhåller sig till .
Om vektorn har ett positivt -element måste även enhetsvektorn ha det, de pekar ju åt samma håll!
Vi kan normera vektorn . Då blir det
eftersom . Är du med?
Vidare, vi säker alltså normalen som pekar "uppåt", eftersom det i uppgiften står att vi söker flödet "i riktning uppåt -axel"
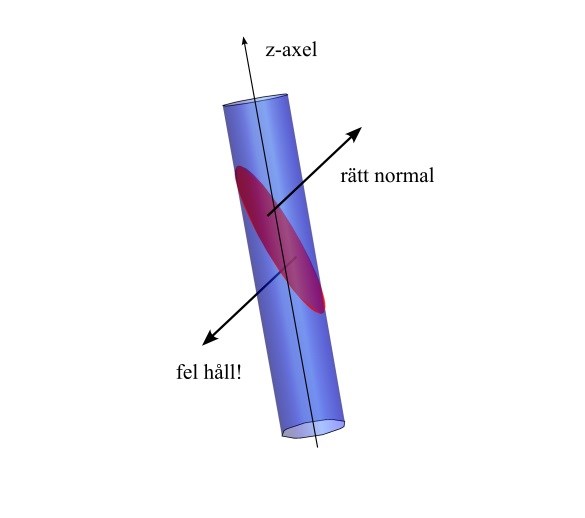
Ah, nu är jag med! Jag förvirrade mig själv lite men nu är jag med till 100 %!
Tack för all hjälp! :D




