Hur ska man tänka med funktionalberoenden i termodynamiska potentialer?
Hej!
Jag håller på att studera termodynamiska potentialer (Legendretransformationer av den interna energin) men jag har lite svårt att få grepp om hur det funktionella beroendet hos den transformerade funktionen ska se ut. Nedan följer en enkel härledning av Helmholtz fria energi, som förhoppningsvis kan tjäna som underlag för eventuell diskussion.
Låt oss anta att vi har ett enkelt system med ett kemiskt species som lyder ekvationen , där är substansmängden av vårt species. Låt oss anta att vi önskar transformera kurvan med avseende på entropin, så att vi erhåller Helmholtz fria energi.
Rent intuitivt kan vi antingen välja att se som mängden av alla punkter som satisfierar , men vi skulle också kunna betrakta funktionen som enveloppen av alla tangenthyperplan till funktionen . Med andra ord vet vi lika mycket om kurvan (givna vissa, implicita antaganden) om vi känner alla tangenthyperplan till som om vi kände till punktmängden.
För illustrationens skull kan vi för tillfället tänka att . Studera figuren nedan, som åskådliggör en tänkt kurva och en tangentlinje som tangerar i punkten :
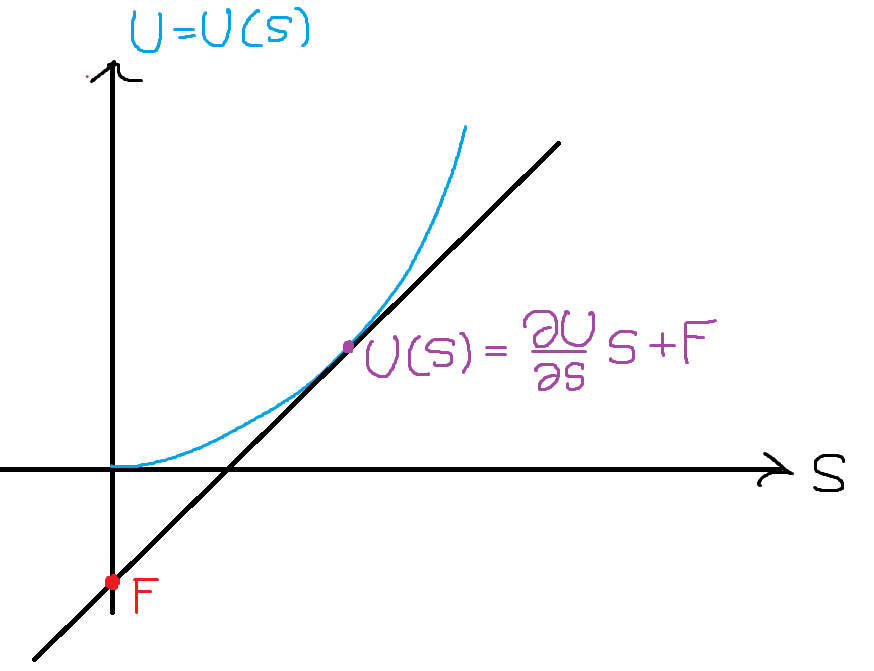
Om vi löser ut ur ekvationen ovan och sätter tillbaka våra tidigare variabler erhåller vi
Hittills har vi bara skrivit om funktionen utan att göra någon variabeländring. Skulle man kunna kalla det ovanstående Helmholtz fria energi, eller kallas den endast detta då man har bytt ut mot som oberende variabel?
Ofta skrivs t.ex. Helmholtz fria energi som , men här finns det inget som anger hur variabelberoendet ser ut så hur ska man veta om de oberende variablerna är , eller kanske extremt exotiskt ? Kallas det för Helmholtz fria energi i alla dessa fall eller är det endast när man har bytt ut den aktuella variabeln mot dess konjugat (entropin mot temperaturen) som funktionen kallas för Helmholts fria energi?


