Hur ska man veta "riktningen" på rörelsemängdsmoment på ett snurrande hjul?
Halloj!
Jag satt med uppgiften nedan:
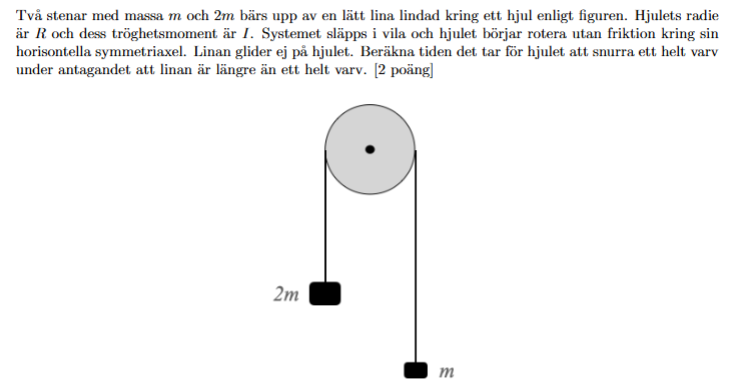
Min lösning framgår i bilden nedan:

Jag har nu en fråga. Sambandet gäller ju i detta fall magnituden av och . Jag har som synes i min bild definierat rörelse nedåt (i den tyngre stenens rörelseriktning) som positiv så då blev storleken rörelsemängdsmomenten av för de två stenarna samt . Till denna summa adderade jag "rörelsemängdsmomentet" för hjulet, . Men har denna någon "riktning"? Jag tänkte att hjulet snurrar "åt samma håll" som stenarna rör sig, dvs. vi borde ha positivt tecken, men jag vet inte... Min fråga är alltså hur jag ska veta att man ska lägga till hjulets rörelsemängdsmoment (vilket jag gjorde) istället för att subtrahera det.
När du summerar, vad du får tänka på är kropparnas rotationsriktning. Vad man får göra först är att definera en positiv riktning för rotation. Det är ju rimligt om den är samma som själva rörelseriktningen för föremålen.  Om ett föremål rör sig medurs så subtraherar vi rörelsemängdsmomentet.
Om ett föremål rör sig medurs så subtraherar vi rörelsemängdsmomentet.
Inte den bästa förklaringen, du får säga till om du tycker det är otydligt.
Vänta nu, jag tror att jag fattar.
Om man tänker på vilken riktning vektorerna kommer ha måste ju rörelsemängdsmomentet för hjulet peka ut mot oss (enligt "skruvregeln"). Då har vi implicit bestämt att "ut mot oss = positiv -riktning". På samma sätt måste kryssprodukten av massornas rörelsemängder och ortsvektorn från rotationsaxeln peka antingen in eller ut ur planet, och eftersom vi har definierat positivt som ut mot oss måste dessa också ha positiva rörelsemängdsmoment.
Eller annorlunda tänkt:
Om man tänker att tråden är jättekort och massorna precis ligger på kanten av hjulet och släpps därifrån, då ger "skruvregeln" återigen att båda massornas rörelsemängdsmoment måste peka i samma riktning som hjulets.
Tillägg: 20 maj 2025 19:58
Kan man tänka på båda dessa sätt?
Här kommer ännu ett inlägg efter lite mer eftertanke. Vi vet för hjulet att:
Om vinkeln nu är sådan att den ökar då vi rör oss moturs kommer vinkelhastigheten att vara positiv, så den pekar då i den riktning vi bestämmer är positiv, säg ut ur planet.
Om vi vidare bestämmer att rörelseriktningen för massorna, alltså nedåt i -led, är positiv, erhåller vi för båda massorna:
Vi vet att kryssprodukten kommer ge en vektor som pekar antingen ut mot oss eller bort in i planet, och eftersom vi har bestämt redan att positiv -riktning är mot oss och är positivt får vi vektorer som pekar ut mot oss, alltså precis i samma riktning som för hjulet. Så om vi vill lägga ihop deras storlekar så adderar vi.
Är det rätt uppfattat?
Man kan alltid tänka att man ska addera och låta hur man definierar sina riktningar och således vektorer styra vilket tecken det blir. Det är en av de största styrkorna med kryssprodukten. Den tar hand om alla tecken automatiskt.
Hmm.
Låt säga då att jag väljer ett koordinatsystem med axlar som definieras av pilarna här:

Blir det så här då för rörelsemängdsmomenten?

Tillägg: 20 maj 2025 21:37
Och på motsvarande sätt när man vill beräkna momenten på klossarna så ser man att den till vänster får ett moment som pekar i positiv -riktning och den till höger får ett moment som pekar i negativ -riktning, så massan till höger får negativt belopp?
Precis så ja.



