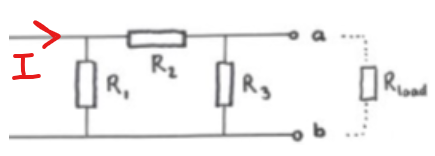
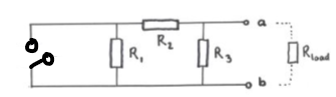
Hur vet man vilka resistorer som sitter parallellt och vilka som sitter i serie, Thévenin?
Halloj!
Jag sitter med uppgiften nedan:
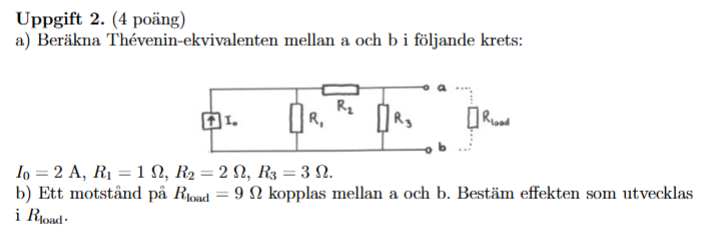
Jag har förstått att det första steget är att tänka bort strömkällan helt. Sedan ska man räkna ut ersättningsresistansen i kretsen "sett från a och b". Jag har väldigt svårt att förstå vad detta betyder. Hur ska man veta vilka resistorer som sitter i serie och vilka som sitter parallellt? Enligt facit sitter tydligen och i serie "sett från a och b", men sitter inte också i serie med , eller likaså och ?
Generellt har jag lite problem med att förstå hur man ska avgöra om två komponenter sitter parallellt eller inte. Kan man tänka att de sitter parallellt om deras ändar är i direkt kontakt, utan någon komponent "i vägen" mellan något par av ändar?
Hej!
Svaret på din sista fråga är ja. Svarar det på din fråga om vilka resistorer som är seriekopplade?
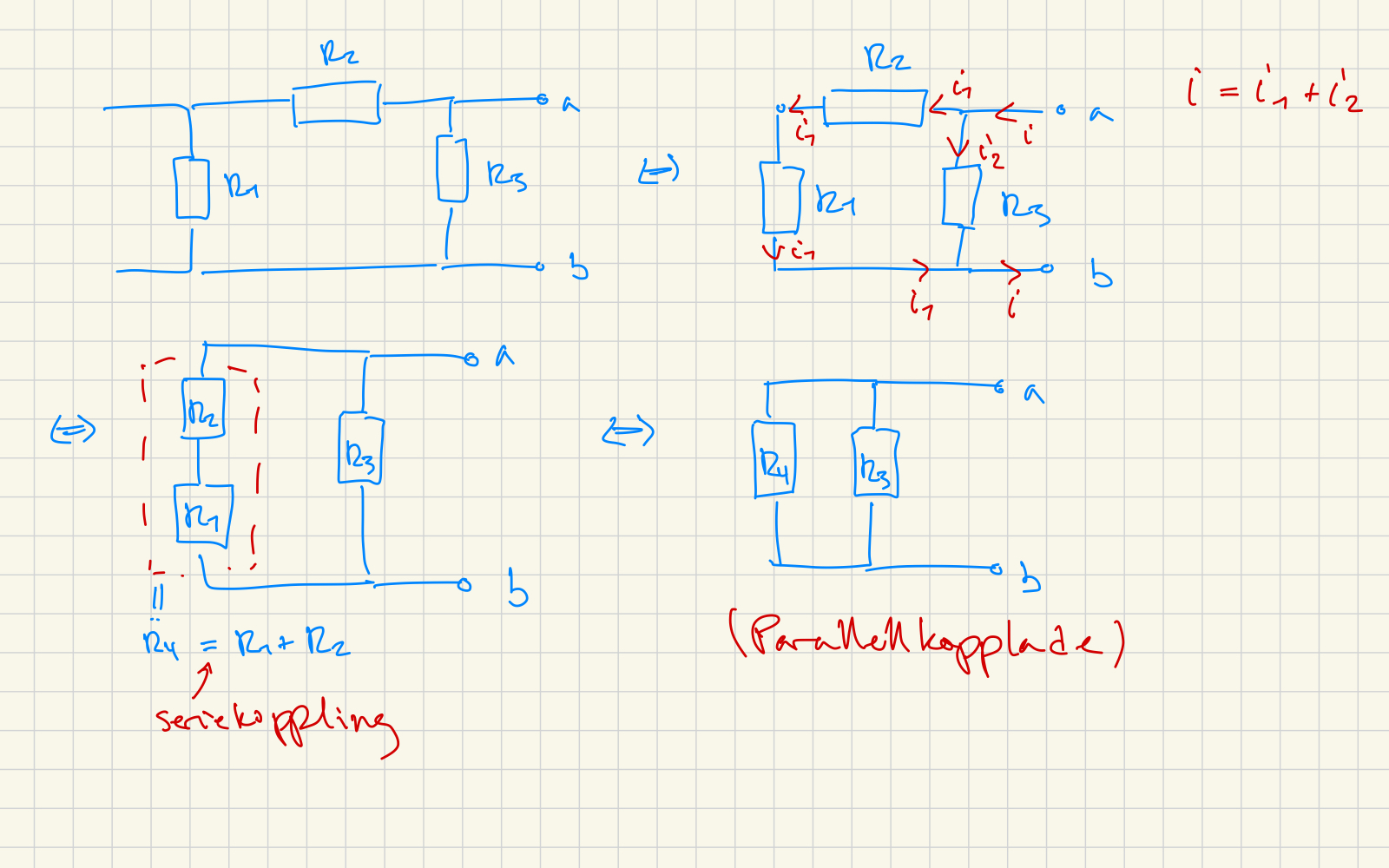
Definitionen av parallellkoppling är att det ligger samma spänning över komponenterna. Det gör det, precis som du säger, om ändarna är i kontakt. Min gamla elläralärare tipsade om att se ledarna i ett kopplingsdiagram som "gummiband". Sen drar man mentalt i 'a' och 'b' i det här fallet så ser man lättare vad som är i serie och parallellt. Här är en bild som jag gjorde till ett gammalt svar här på PA:

Oftast kan man se hela kretsen som en kombination av serie- och parallellkopplingar, och då arbetar man lättast inifrån och ut. Om jag kallar seriekoppling för + och parallellkoppling för // så kan kretsen i föregående inlägg beskrivas som
(A+B)//(C+(D//(E+F)))
Man kan räkna ut ersättningsresistansen som resultatet av detta uttryck, om man definierar a//b som 1/(1/a + 1/b).
Svaret på din sista fråga är ja. Svarar det på din fråga om vilka resistorer som är seriekopplade?
I så fall finns det väl flera par av resistorer i min krets som är seriekopplade? 1 och 3, 2 och 3 samt 1 och 2? Jag förstår inte riktigt vad det här med "sett från a och b" ska innebära...?
I facit har man valt att se två av resistoerna som seriekopplade och räknat ut en ersättningsresistans för dessa, och sedan räknat att denna ersättningsresistor sitter parallellt med den tredje. Men vilket par ska man välja för att räkna ut "seriersättningsresistansen"? Kan man välja vilket par man vill?
Strömkällan tar du först bort. Då får du denna krets

Samma ström kommer att flyta i R1 och R2, vilket är definitionen för seriekopplade element. Samma spänning kommer att ligga över R3 och ersättningsresistansen för R1-R2, vilket är definitionen för parallellkoppling.
Men varifrån kommer den strömmen om det inte finns någon strömkälla? Jag förstår inte biten "sett från a och b".
naytte skrev:Men varifrån kommer den strömmen om det inte finns någon strömkälla?
Relevant kommentar! Jag skulle ha skrivit "om det hade flutit en ström genom R1, skulle samma ström flyta genom R2, etc."
"om det hade funnits en spänning över R2, skulle samma spänning finnas över... etc"
Jag förstår inte biten "sett från a och b".
Också relevant! Jag tror du skulle kunna se det som "oberoende av vad du sedan ansluter mellan a och b" Dvs om du ansluter en Rload mellan a och b så kommer fortfarande samma ström (om den hade funnits) att flyta genom R1 och R2. Och samma spänning (om den hade funnits) att ligga över R3 och ...
Men om en ström skulle flyta genom , så skulle väl samma ström också flyta genom ? Och samma sak gäller vä även och ? Det beror väl på åt vilket håll strömmen går?
naytte skrev:Men om en ström skulle flyta genom , så skulle väl samma ström också flyta genom ? Och samma sak gäller vä även och ? Det beror väl på åt vilket håll strömmen går?
Om du har anslutit en Rload så kommer inte samma ström att flyta i R3 som i R2, eller hur?
Nej men det hade väl inte nödvändigtvis gått samma ström genom och då heller? Beroende på varifrån den tänkta strömmen kommer, menar jag. T.ex. här får vi väl inte samma ström genom och ?
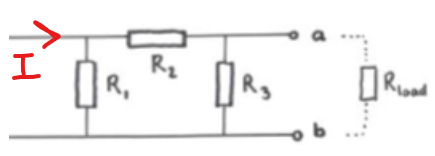
Det har du rätt i. Men i det här fallet så är det "sett ifrån a och b". Alltså om du skickar in strömmen (eller spänningen) därifrån.
Jag förstår att det kan kännas förvirrande att jag skriver "som om" hela tiden. Men det är just det som Thevenin - och Norton ekvivalenterna går ut på, att man ska kunna förenkla en krets och kunna använda förenklingen oavsett vad som kopplas till den.
(Lite överspelad metodik numera kanske då man enkelt simulerar kretsen med dator utan förenklingar)
naytte skrev: ...tänka bort strömkällan helt. Sedan ska man räkna ut ersättningsresistansen i kretsen "sett från a och b".
Är det inte tydligt med "gummibandstänket" att R3 är parallell med (R1+R2)? Hugg tag i 'a' och dra uppåt och hugg tag i 'b' och dra nedåt.
Det är som att koppla en ohmmätare till a och b med strömkällan borttagen. I praktiken kommer ohmmätaren att skicka en liten ström mellan a och b genom resistorerna enligt kirchoffs strömlag och ohms lag.
naytte skrev:Nej men det hade väl inte nödvändigtvis gått samma ström genom och då heller? Beroende på varifrån den tänkta strömmen kommer, menar jag. T.ex. här får vi väl inte samma ström genom och ?
Det som kan förvirra är att du tror att det kan gå ström i de grenarna som sticker ut till vänster. Men där är kretsen bruten så strömmen är 0. Om vi då tar en ström från a som delar sig i R2 och R3 kommer all ström som går genom R2 fortsätta genom R1.
Okej, jag tror att jag är med. Så det man menar med "sett från a och b" är "om vi låtsas som om strömmen antingen kommer från punkten a eller punkten b"
Det är ingen definition men det är så många tänker vet jag.
Okej, tack! Då kör jag på det och ber en bön om att det är allmängiltigt.
MrPotatohead skrev:Det är ingen definition men det är så många tänker vet jag.
Precis. Det är en hemsnickrad definition för att kunna förklara seriekoppling och parallellkoppling med deras definitioner. Det fungerar som gummibandet (som också är jättebra)
En fråga till. Då vi tänker bort strömkällan, tänker vi att kretsen är öppen där, så att ingen ström kan gå där alls? Alltså:
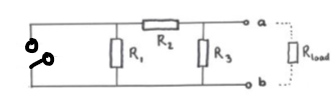
Precis! På liknande sätt blir en spänningskälla en kortslutning när den nollställs. Notera att detta endast kan göras om de är oberoende.
Man kan kanske se det som att "sett från a och b" innebär att vi bara har 2 sladdar som sticker ut från en svart låda och vårt uppdrag är att rekonstruera den svarta lådan med alla dess egenskaper?
naytte skrev:En fråga till. Då vi tänker bort strömkällan, tänker vi att kretsen är öppen där, så att ingen ström kan gå där alls? Alltså:
Som mrp antydde, teorin bakom Thevenin- och Norton-ekvivalenterna. Eftersom det bara handlar om linjära och oberoende element behöver man bara hitta _en_ inställning på källorna där det är enkelt att matcha ett förenklat nät med det verkliga nätet. Som enklast är det när källor är nollställda. En strömkälla som driver 0A är per definition en öppen krets, och en spänningskälla som driver 0V är per definition en kortslutning. Alltså ersätts källorna med öppenkretsar och kortslutningar när man räknar ut den ekvivalenta resistansen. Har man väl fått ordning på just den källinställningen kan man vara säker på att alla andra källinställningar också stämmer.