Hur visar man att derivatan av trycket är oberoende av z?

Hej!

Jag håller på att studera ett elementärt exempel i fluiddynamik där man har en isotrop, Newtonsk fluid som strömmar laminärt och stadigt (ingen acceleration) mellan två parallella plattor med oändlig utbredning. Se schematisk figur nedan:

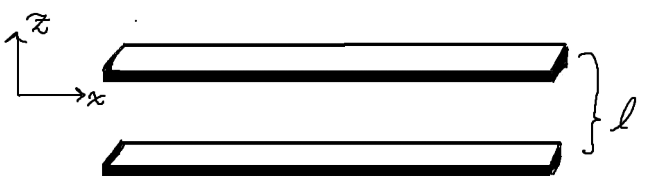
Koordinatsystemet är lagt så att positiv $y$-riktning pekar rakt in bilden och är ortogonal mot $xz$-planet och fluiden strömmar endast i positiv $x$-riktning. Målet är att härleda hastighetsprofilen i fluiden som en funktion av de spatiala koordinaterna $(x,y,z)$.

Jag påbörjade min analys genom att studera ett infinitesimalt fluidelement någonstans i fluiden. Efter lite analys med Newtons andra lag och förenklingar lyckades jag komma fram till följande differentialekvation för alla punkter $(x,y,z)$,

$\displaystyle \frac{\partial^2 v}{\partial z^2}=\frac{\partial P}{\partial x}$

För att lösa ut hastigheten vill vi integrera två gånger med avseende på $z$ och sedan använda randvillkor. Svaret kräver att man antar att $\partial_x P$ är oberoende av $z$, så att det bara blir en konstnat vid integrering. Men hur motiverar man detta?