Infimum och supremum
Hej,
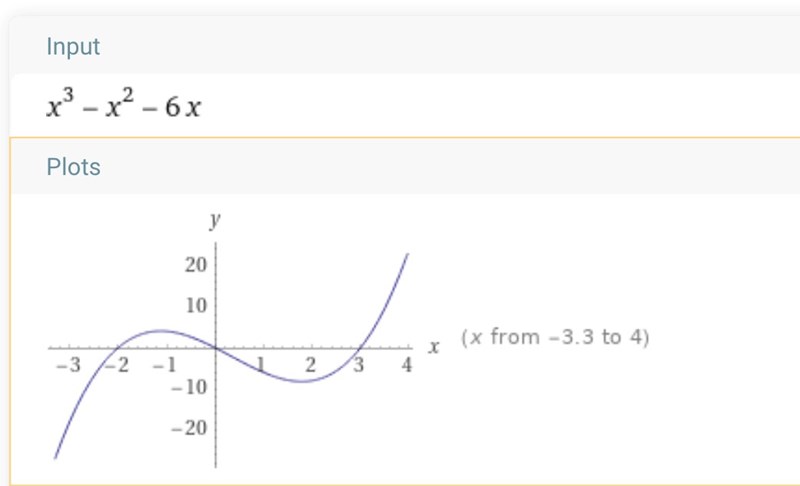
Jag undrar lite kring supremum och maximum av en mängd , supremum hittade jag kanska enkelt då är växande för x som är större än 3 så , men däremot har jag det lite svårare med supremum.
Då funktionen måste vara större än noll kan den inte anta x-värden som är lika med -2 eller mindre, inte heller kan den anta x-värden som är lika med noll upp till tre. Funktionen går mot 0 då eller , ska då denna anses som ett infimum som inte tillhör mängden M? Eller ska 4 anses som ett infimum då funktionen går mot 4 då och vi har att ?
Din slutsats om supremumet är korrekt men din motivering lite oklar. Det räcker inte att säga att funktionen är växande för alla x>3.
Din diskussion om infimum får mig att tro att du kanske missuppfattat lite. När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x.
Notera att M = (-2, 0)(3, ).
Vidare så gäller det att inf = inf{infA, infB}.
Smutsmunnen skrev:Din slutsats om supremumet är korrekt men din motivering lite oklar. Det räcker inte att säga att funktionen är växande för alla x>3.
Din diskussion om infimum får mig att tro att du kanske missuppfattat lite. När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x.
Hej, tack för svar! Skulle du kunna utveckla vad du menar med att När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x? För till exempel för funktion på intervallet [1,] så är infimum = sin(1) och supremum = 1 och detta är väl värden för funktionen och inte för x?
Med andra ord, i detta fall är det väl som ger oss de x-värden som finns i mängden?
lund, kan du beskriva med ord vilka element som ingår i mängden M?
Du undrar lite kring supremum och maximum. En mängd M som är uppåt begränsad har enligt supremumaxiomet en minsta övre begränsning. Denna kallas supremum av M och förkortas sup M. Sup M kan tillhöra M, men behöver inte göra det. Ex.: Låt M = mängden av x sådana att 0<x<1. Här är x=2 EN ÖVRE BEGRÄNSNING till M, men inte den minsta. Den minsta övre begränsningen är sup M= =1, men 1 tillhör inte M. Till skillnad från sup M måste ett maximum även kallat maximalt element i M alltid tillhöra M. I detta fall har M inget maximalt element, men eftersom M är begränsad uppåt har den ett supremum.
Smaragdalena skrev:lund, kan du beskriva med ord vilka element som ingår i mängden M?
De element som ingår i mängden M är de som för reella x ges utav och som är större än noll. Dessa blir blandannat och fortsätter mot oändligheten.
lund skrev:Smutsmunnen skrev:Din slutsats om supremumet är korrekt men din motivering lite oklar. Det räcker inte att säga att funktionen är växande för alla x>3.
Din diskussion om infimum får mig att tro att du kanske missuppfattat lite. När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x.
Hej, tack för svar! Skulle du kunna utveckla vad du menar med att När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x? För till exempel för funktion på intervallet [1,] så är infimum = sin(1) och supremum = 1 och detta är väl värden för funktionen och inte för x?
Med andra ord, i detta fall är det väl som ger oss de x-värden som finns i mängden?
Notationen
kallas set-builder notation. Det ska tolkas som "den delmängd av R för vilka villkoret efter kolonet gäller".
Du kan om du vill läsa om set-builder notation här om du vill:
https://en.wikipedia.org/wiki/Set-builder_notation
Kontentan är i vart fall att det inte är funktionen efter kolonet vars inf/sup vi söker utan alltså "inf/sup bland de reella som x som uppfyller olikheten efter kolonet"-
Smutsmunnen skrev:lund skrev:Smutsmunnen skrev:Din slutsats om supremumet är korrekt men din motivering lite oklar. Det räcker inte att säga att funktionen är växande för alla x>3.
Din diskussion om infimum får mig att tro att du kanske missuppfattat lite. När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x.
Hej, tack för svar! Skulle du kunna utveckla vad du menar med att När vi söker infimum och supremum söker vi största största och minsta värden på x, inte största och minsta värden på x^3-x^2-6x? För till exempel för funktion på intervallet [1,] så är infimum = sin(1) och supremum = 1 och detta är väl värden för funktionen och inte för x?
Med andra ord, i detta fall är det väl som ger oss de x-värden som finns i mängden?
Notationen
kallas set-builder notation. Det ska tolkas som "den delmängd av R för vilka villkoret efter kolonet gäller".
Du kan om du vill läsa om set-builder notation här om du vill:
https://en.wikipedia.org/wiki/Set-builder_notation
Kontentan är i vart fall att det inte är funktionen efter kolonet vars inf/sup vi söker utan alltså "inf/sup bland de reella som x som uppfyller olikheten efter kolonet"-
Stort tack! I detta fall bör då , och denna lika med noll får vi det minsta värdet på x som -2, om jag förstår det rätt nu.
Men hur bör man då istället motivera att , kan man säga att då olikheten gäller för alla x som är större än 3 så kommer supremum, det vill säga det största möjliga värdet för x, att vara oändligheten?
Ja precis, "olikheten gäller för alla x i så sup är ."
Tack så mycket för din hjälp! Då har jag verkligen förstått detta.
Blir inte inf M = 3 eftersom infinumet är den största minoranten i mängden?
sofie123 skrev:Blir inte inf M = 3 eftersom infinumet är den största minoranten i mängden?
Nä inf M blir inte 3 eftersom 3 inte är en minorant till mängden. Exvis hör -1 till mängden. Se Patenterameras inlägg i tråden.


